Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T17:49:32.520Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Automorphisms of a Finite p-group

Published online by Cambridge University Press:  20 November 2018

Theodoros Exarchakos
Theodoros Exarchakos*
Affiliation:
Koridallos, Athens, Greece
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we find a new bound for the function g(h), for which |A(G)|p ≧ pn whenever |G| ≧ pg(h) G a finite p-group. The existence of such a function was first conjectured by W. R. Scott in 1954, who proved that g (2) = 3. In 1956 Ledermann and Neumann proved that in the general case of finite groups g(h) ≦ (h – 1)3.-pn−1 + h[10]. Since then, J. A. Green, J. C. Howarth and K. H. Hyde have reduced this bound considerably. The best (least) bound to date for finite p-groups was obtained by K. H. Hyde [9]. He proved that 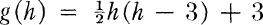for h ≧ 5 and g(h) = h + 1 for h ≦ 4. For finite non-abelian p-groups, we improve this bound to: 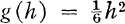for h ≧ 13, g(h) = 2h – 5 for 5 < h ≦ 8, g(h) = h for h ≦ 5 and for 8 < h ≦ 12 we prove that g(9) = 14, g(10) = 17, g(11) = 20, g(12) = 23.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1448 - 1458
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Adney, J. E. and Yen, Ti, Automorphisms of a p-group, Illinois J. Math. 9 (1965), 137–143.Google Scholar
2. Blackburn, N., On a special class of p-groups, Acta Math. 100 (1958), 45–92.Google Scholar
3. Blackburn, N., On prime-power groups with two generators, Proc. Camb. Phil. Soc. 54 (1958), 327–337.Google Scholar
4. Buckley, J., Automorphism groups of isoclinic p-groups, J. London Math. Soc. 12 (1975), 37–44.Google Scholar
5. Faudree, R., A note on the automorphism group of a p-group, Proc. Amer. Math. Soc. 19 (1968), 1379–1382.Google Scholar
6. Gaschütz, W., Nichtabelsche p-Gruppen besitzen dussere p-Automorphismen, J. of Algebra 4 (1966), 1–2.Google Scholar
7. Hummel, K. G., The order of the automorphism group of a central product, Proc. Amer. Math. Soc. 47 (1975), 37–40.Google Scholar
8. Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin, Heidelberg, 1967).CrossRefGoogle Scholar
9. Hyde, K. H., On the order of the Sylow subgroups of the automorphism group of a finite group, Glasgow Math. J. 11 (1970), 88–96.Google Scholar
10. Ledermann, W. and Neumann, B. H., On the order of the automorphism group of a finite group II, Proc. Roy. Soc. Ser. A. 235 (1956), 235–246.Google Scholar