Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-03T02:48:56.022Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hyperinvariant Subspace Problem. IV

Published online by Cambridge University Press:  20 November 2018

H. Bercovici ,
C. Foias  and
C. Pearcy
H. Bercovici
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, U.S.A. e-mail:[email protected]
C. Foias
Affiliation:
Department of Mathematics Texas A&M University College Station, TX 77843 U.S.A. e-mail:[email protected]
C. Pearcy
Affiliation:
Department of Mathematics Texas A&M University College Station, TX 77843 U.S.A. e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is a continuation of three recent articles concerning the structure of hyperinvariant subspace lattices of operators on a (separable, infinite dimensional) Hilbert space 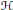$\mathcal{H}$. We show herein, in particular, that there exists a “universal” fixed block-diagonal operator 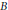$B$ on 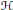$\mathcal{H}$ such that if 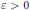$\varepsilon >0$ is given and 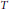$T$ is an arbitrary nonalgebraic operator on 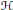$\mathcal{H}$, then there exists a compact operator 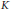$K$ of norm less than $\varepsilon $ such that (i) Hlat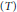$(T)$ is isomorphic as a complete lattice to Hlat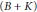$(B+K)$ and (ii) 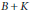$B+K$ is a quasidiagonal, 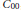${{C}_{00}}$, 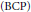$(\text{BCP})$-operator with spectrum and left essential spectrum the unit disc. In the last four sections of the paper, we investigate the possible structures of the hyperlattice of an arbitrary algebraic operator. Contrary to existing conjectures, Hlat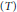$(T)$ need not be generated by the ranges and kernels of the powers of 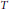$T$ in the nilpotent case. In fact, this lattice can be infinite.

Keywords

47A15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 4 , 01 August 2008 , pp. 758 - 789
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Apostol, C., Douglas, R. G., and C. Foias, Quasi-similar models for nilpotent operators. Trans. Amer. Math. Soc. 224(1976), no. 2, 407–415.Google Scholar
[2] Apostol, C., Fialkow, L., Herrero, D., and Voiculescu, D., Approximation of Hilbert space operators. Vol. II. Research Notes in Mathematics 102. Pitman (Advanced Publishing Program), Boston,MA, 1984.Google Scholar
[3] Barraa, M., Sous-espaces hyperinvariants d’un opérateur nilpotent sur un espace de Banach. J. Operator Theory 21(1989), no. 2, 315–321.Google Scholar
[4] Barria, J. and Herrero, D., Closure of similarity orbits of Hilbert space operators. IV. Normal operators. J. LondonMath. Soc. 17(1978), no. 3, 525–536.Google Scholar
[5] Bercovici, H., C0-Fredholm operators. II. Acta Sci. Math. (Szeged) 42(1980), no. 1-2, 3–42.Google Scholar
[6] Bercovici, H., A note on disjoint invariant subspaces , MichiganMath. J. 34(1987), no. 3, 435–439.Google Scholar
[7] Bercovici, H., Operator theory and arithmetic in H∞. Mathematical Surveys and Monographs 26, American Mathematical Society, Providence, RI, 1988.Google Scholar
[8] Bercovici, H., Foias, C., and Pearcy, C., Dilation theory and systems of simultaneous equations in the predual of an operator algebra. I. Michigan Math. J. 30(1983), no. 3, 335–354.Google Scholar
[9] Bercovici, H., Foias, C., and C. Pearcy, Dual algebras with applications to invariant subspaces and dilation theory, CBMS Regional Conference Series in Mathematics 56, American Mathematical Society, Providence, RI, 1985.Google Scholar
[10] Charles, B., Opérateurs linéaires sur un espace de Banach et modules sur un anneau principal. In: Symposia Mathematica 23, Academic Press, London, 1979, pp. 121–143.Google Scholar
[11] Fillmore, P. A., Herrero, D. A., andLongstaff, W. E., The hyperinvariant subspace lattice of a lineartransformation. Linear Algebra and Appl. 17(1977), no. 2, 125–132.Google Scholar
[12] Foias, C., Invariant para-closed subspaces. Indiana Univ.Math. J. 21(1971/72), 887–906.Google Scholar
[13] Foias, C., Hamid, S., Onica, C., and C. Pearcy, On the hyperinvariant subspace problem. III. J. Funct. Anal. 222(2005), no. 1, 129–142.Google Scholar
[14] Foias, C., S.-C. Ong, and P. Rosenthal, An interpolation theorem and operator ranges. Inegral Equations Operator Theory 10(1978), no. 6, 802–811.Google Scholar
[15] Foias, C. and C. Pearcy, On the hyperinvariant subspace problem. J. Funct. Anal. 219(2005), no. 1, 134–142.Google Scholar
[16] Fuchs, L., Infinite abelian groups. Pure and Applied Mathematics 36-II. Academic Press, New York, 1973.Google Scholar
[17] Hamid, S., Onica, C., and C. Pearcy, On the hyperinvariant subspace problem. II. Indiana Univ.Math. J. 54(2005), no. 3, 743–754.Google Scholar
[18] Herrero, D. A., Quasisimilarity does not preserve the hyperlattice. Proc. Amer.Math. Soc. 65(1977), no. 1, 80–84.Google Scholar
[19] Herrero, D. A., Approximation of Hilbert space operators. Second edition. Pitman Research Notes in Mathematics Series 224, John Wiley, New York, 1989.Google Scholar
[20] Kaplansky, I., Infinite Abelian Groups. University of Michigan Press, Ann Arbor,Michigan, 1954.Google Scholar
[21] Paulsen, V., Completely bounded maps and dilations. Pitman Research Notes in Mathematics Series 146, John Wiley, New York, 1986.Google Scholar
[22] Peetre, J., On an interpolation theorem of Foias and Lions. Acta Sci. Math. (Szeged) 25(1964), 255–261.Google Scholar
[23] Peetre, J., On interpolation functions , Acta Sci. Math. (Szeged) 27(1966), 167–171.Google Scholar
[24] Radjavi, H. and Rosenthal, P., Invariant subspaces, Ergebnisse derMathematik und ihrer Grenzgebiete 77, Springer-Verlag, New York, 1973.Google Scholar
[25] Williams, L., Similarity invariants for a class of nilpotent operators. Acta Sci. Math. (Szeged) 38(1976), no. 3-4, 423–428.Google Scholar