Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T19:03:36.613Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Matrix Theoremsof Frobenius and McCoy

Published online by Cambridge University Press:  20 November 2018

J. K. Goldhaber  and
G. Whaples
J. K. Goldhaber
Affiliation:
University of Connecticut
G. Whaples
Affiliation:
Indiana Unwersity
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

McCoy, following Frobenius, studied a problem which can be described as follows. Let k be an arbitrary field, kc its algebraic closure, and 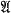any algebra of n ⨯ n matrices over k which contains the identity I . Define a canonical ordering to be a set of n mappings λ of 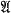, or of a subset 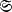of 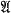, into kc such that the sequence λ1(A),λ2(A), …, λn(A), for each A ∈ 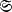, consists of the characteristic values (roots of det(A — xI) = 0) of A, each with the right multiplicity. Define a canonical ordering to be a Frobenius ordering if, for all non-commutative polynomials f(x1, x2, … , xm) and all finite subsets A1, A2, …, Am of ,

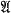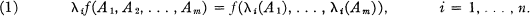
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 5 , 1953 , pp. 332 - 335
Copyright
Copyright © Canadian Mathematical Society 1953

References

1. Albert, A. A., Structure of algebras (New York, 1946).Google Scholar
2. Artin, E. and Whaples, G., The theory of simple rings, Amer. j . Math., 65 (1943), 87–107.Google Scholar
3. Deuring, M., Algebren (Ergebnisse der Math., vol. 4, Berlin, 1935).Google Scholar
3a. Frobenius, G., fiber vertauschbare Malrizen, Sitz. preuss. Akad. Wiss. (1896), 601–614.Google Scholar
4. Goldhaber, J. K., The homomorphic mapping of certain matric algebras onto rings of diagonal matrices, Can. J. Math., 4 (1952), 31–42.Google Scholar
5. McCoy, N. H., On the characteristic roots of matric polynomials, Bull. Amer. Math. Soc, 42 (1936), 592–600.Google Scholar
6. van der Waerden, B. L., Moderne Algebra, 2nd ed., vol. 1 (Berlin, 1937).Google Scholar