Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kaplansky, Irving
1953.
Infinite-dimensional quadratic forms admitting composition.
Proceedings of the American Mathematical Society,
Vol. 4,
Issue. 6,
p.
956.
Schafer, R. D.
1955.
Structure and representation of nonassociative algebras.
Bulletin of the American Mathematical Society,
Vol. 61,
Issue. 6,
p.
469.
Paige, Lowell J.
1956.
A class of simple Moufang loops.
Proceedings of the American Mathematical Society,
Vol. 7,
Issue. 3,
p.
471.
Kleinfeld, Erwin
1962.
Associator dependent rings.
Archiv der Mathematik,
Vol. 13,
Issue. 1,
p.
203.
Humm, Margaret M.
and
Kleinfeld, Erwin
1966.
On extensions of Cayley algebras.
Proceedings of the American Mathematical Society,
Vol. 17,
Issue. 5,
p.
1203.
1966.
Vol. 22,
Issue. ,
p.
149.
Humm, Margaret M
1967.
On a class of right alternative rings without nilpotent ideals.
Journal of Algebra,
Vol. 5,
Issue. 2,
p.
164.
Sterling, Nicholas J.
1967.
Prime associator-dependent rings with idempotent.
Transactions of the American Mathematical Society,
Vol. 128,
Issue. 3,
p.
474.
Zhevlakov, K. A.
1969.
On radicals and von Neumann ideals.
Algebra and Logic,
Vol. 8,
Issue. 4,
p.
244.
Kleinfeld, Erwin
1971.
Generalization of alternative rings, I.
Journal of Algebra,
Vol. 18,
Issue. 2,
p.
304.
Osborn, J.Marshall
1972.
Varieties of algebras.
Advances in Mathematics,
Vol. 8,
Issue. 2,
p.
163.
Getu, Seyoum
and
Rodabaugh, D.J.
1974.
Generalizing alternative rings.
Communications in Algebra,
Vol. 2,
Issue. 1,
p.
35.
Britten, Daniel J.
1975.
On Cayley-Dickson Rings.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 5,
p.
625.
Thedy, Armin
1975.
Right alternative rings.
Journal of Algebra,
Vol. 37,
Issue. 1,
p.
1.
Hentzel, I.R
Kleinfeld, E
and
Smith, H.F
1980.
Alternative rings with idempotent.
Journal of Algebra,
Vol. 64,
Issue. 2,
p.
325.
1980.
Polynomial Identities in Ring Theory.
Vol. 84,
Issue. ,
p.
341.
Rich, Michael
1982.
Some properties of the Levitzki radical in alternative rings.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 32,
Issue. 1,
p.
52.
1982.
Vol. 104,
Issue. ,
p.
352.
Jacobson, N.
1989.
Nathan Jacobson Collected Mathematical Papers.
p.
173.
Jacobson, N.
1989.
Nathan Jacobson Collected Mathematical Papers.
p.
179.
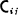 where
where  . The elements e11 and e00 are orthogonal idempotents an
. The elements e11 and e00 are orthogonal idempotents an  ,
, 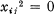 for every xij of
for every xij of 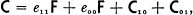 . The multiplication table of C is then completed by the relations
. The multiplication table of C is then completed by the relations

