Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T19:21:06.066Z Has data issue: false hasContentIssue false
  • English
  • Français

On Reflexivity of Algebras

Published online by Cambridge University Press:  20 November 2018

Mehdi Radjabalipour
Mehdi Radjabalipour*
Affiliation:
University of Mazandaran, Babolsar, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each natural number n we define to be the class of all weakly closed algebras 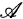of (bounded linear) operators on a separable Hilbert space H such that the lattice of invariant subspaces of and (alg lat 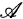)(n) are the same. (If A is an operator, A(n) denotes the direct sum of n copies of A; if 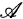is a collection of operators,. Also, alg lat 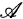denotes the algebra of all operators leaving all invariant subspaces of 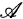invariant.) In the first section we show that 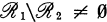. In Section 2 we prove that every weakly closed algebra containing a maximal abelian self adjoint algebra (m.a.s.a.) is 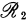, and that . It is also shown that certain algebras containing a m.a.s.a. are necessarily reflexive.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1291 - 1308
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Arveson, W. B., A density theorem for operator algebras, Duke Math. J. 34 (1976), 635–647.Google Scholar
2. Arveson, W. B., Operator algebras and invariant subspaces, Annals Math. 100 (1974), 433–532.Google Scholar
3. Azoff, E. A., K-reflexivity infinite dimensional spaces, Duke Math. J. 40 (1973), 821–830.Google Scholar
4. Cater, F. S., Lectures on real and complex vector spaces, (W. B. Saunders, Philadelphia, 1966).Google Scholar
5. Deddens, J. and Fillmore, P., Reflexive linear transformations, Lin. Alg. Appl. 10 (1975), 89–93.Google Scholar
6. Douglas, R. G. and Pearcy, C., Hyperinvariant subspaces and transitive algebras, Michigan Math. J. 19 (1972), 1–12.Google Scholar
7. Dunford, N. and Schwartz, J., Linear operators. Part II: Spectral theory, (Interscience, New York, 1963).Google Scholar
8. Feintuch, A., There exist nonreflexive inflations, Michigan Math. J. 21 (1974), 13–17.Google Scholar
9. Feintuch, A. and Rosenthal, P., Remarks on reductive operator algebras, Israel J. Math. 15 (1973), 130–136.Google Scholar
10. Foias, C., Invariant para-closed subspaces, Indiana Univ. Math. J. 21 (1972), 887–906.Google Scholar
11. Halmos, P. R., A Hilbert space problem book, (D. Van Nostrand, Princeton, New Jersey, 1967).Google Scholar
12. Lomonosov, V. J., Invariant subspaces for operators commuting with compact operators, Functional Anal. Appl. 7 (1973), 55–56.Google Scholar
13. Nordgren, E., Radjabalipour, M., Radjavi, H. and Rosenthal, P., On invariant operator ranges, Trans. Amer. Math. Soc. 251 (1979), 389–398.Google Scholar
14. Nordgren, E., Radjavi, H. and Rosenthal, P., Operator algebras leaving compact operator ranges invariant, Mich. Math. J. 23 (1976), 375–377.Google Scholar
15. Nordgren, E., Radjavi, H. and Rosenthal, P., On Arveson's characterization of hyperreducible triangular algebras, Indiana Univ. Math. J. 26 (1977), 179–182.Google Scholar
16. Radjavi, H. and Rosenthal, P., On invariant subspaces and reflexive algebras, Amer. J. Math. 91 (1969), 683–692.Google Scholar
17. Radjavi, H. and Rosenthal, P., A sufficient condition that an operator algebra be self-adjoint, Can. J. Math. 28 (1971), 588–597.Google Scholar
18. Radjavi, H. and Rosenthal, P., Invariant subspaces, (Springer-Verlag, Berlin-Heidelberg-New York, 1973).Google Scholar
19. Rosenthal, P., On commutants of reductive operator algebras, Duke Math. J. 41 (1974), 829–834.Google Scholar
20. Sarason, D. E., Invariant subspaces and unstarred operator algebras, Pac. J. Math. 17 (1966), 511–517.Google Scholar
21. Sul'man, V. S., On reflexive operator algebras, Math. USSR-Sb. 16 (1972), 181–189.Google Scholar