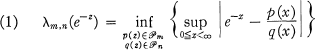Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rahman, Q. I.
and
Schmeisser, G.
1978.
Numerische Methoden der Approximationstheorie.
Vol. 42,
Issue. ,
p.
252.
Borwein, Peter B
1981.
Approximation of xn by reciprocals of polynomials.
Journal of Approximation Theory,
Vol. 32,
Issue. 3,
p.
241.


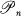 denotes the class of all polynomials of degree at most
denotes the class of all polynomials of degree at most