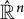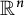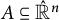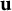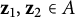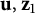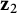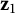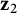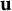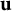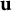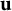1 Introduction
Let
![]() $\mathbb {R}^n$
be the real vector space of dimension n. We compactify
$\mathbb {R}^n$
be the real vector space of dimension n. We compactify
![]() $\mathbb {R}^n$
by adding an
$\mathbb {R}^n$
by adding an
![]() $\infty $
point, and when we say that
$\infty $
point, and when we say that
![]() $\mathbf {u} \rightarrow \infty $
, we mean
$\mathbf {u} \rightarrow \infty $
, we mean
![]() $\|\mathbf {u} \| \rightarrow \infty $
. Denote by
$\|\mathbf {u} \| \rightarrow \infty $
. Denote by
![]() $\hat {\mathbb {R}}^n$
the one-point compactification
$\hat {\mathbb {R}}^n$
the one-point compactification
![]() $\mathbb {R}^n \cup \{\infty \}$
. Throughout this work, we identify the geometric structure of
$\mathbb {R}^n \cup \{\infty \}$
. Throughout this work, we identify the geometric structure of
![]() $\mathbb {C}^n$
with that of
$\mathbb {C}^n$
with that of
![]() $\mathbb {R}^{2n}$
. For example, when we say that something is a hyperplane in
$\mathbb {R}^{2n}$
. For example, when we say that something is a hyperplane in
![]() $\mathbb {C}^n$
, we mean a hyperplane in
$\mathbb {C}^n$
, we mean a hyperplane in
![]() $\mathbb {R}^{2n}$
– that is, an affine subspace of real dimension
$\mathbb {R}^{2n}$
– that is, an affine subspace of real dimension
![]() $2n-1$
. Moreover, we use boldface font to differentiate vectors from scalars.
$2n-1$
. Moreover, we use boldface font to differentiate vectors from scalars.
Take a point
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
and a subset
$\mathbf {u} \in \hat {\mathbb {R}}^n$
and a subset
![]() $A \subset \hat {\mathbb {R}}^n$
. Given any two points
$A \subset \hat {\mathbb {R}}^n$
. Given any two points
![]() $\mathbf {z}_1 , \mathbf {z}_2 \in A$
, different from
$\mathbf {z}_1 , \mathbf {z}_2 \in A$
, different from
![]() $\mathbf {u}$
, there is a unique circle passing through
$\mathbf {u}$
, there is a unique circle passing through
![]() $\mathbf {u}, \mathbf {z}_1,$
and
$\mathbf {u}, \mathbf {z}_1,$
and
![]() $\mathbf {z}_2$
. Denote by
$\mathbf {z}_2$
. Denote by
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2]$
the arc of this circle between
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2]$
the arc of this circle between
![]() $\mathbf {z}_1$
and
$\mathbf {z}_1$
and
![]() $\mathbf {z}_2$
that does not contain
$\mathbf {z}_2$
that does not contain
![]() $\mathbf {u}$
. We say that A is
$\mathbf {u}$
. We say that A is
![]() $\mathbf {u}$
-convex if for every pair of points
$\mathbf {u}$
-convex if for every pair of points
![]() $\mathbf {z}_1, \mathbf {z}_2 \in A$
, the set
$\mathbf {z}_1, \mathbf {z}_2 \in A$
, the set
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2]$
is contained in A. In other words, we say that A is convex with respect to
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2]$
is contained in A. In other words, we say that A is convex with respect to
![]() $\mathbf {u}$
, and we say that
$\mathbf {u}$
, and we say that
![]() $\mathbf {u}$
is a pole for A. The observation that some sets are convex with respect to a pole was made by Pólya and Szegö (see pages 53–56 in [Reference Pólya and Szegö8, Chapter 2]), but to our knowledge, it was not further developed.
$\mathbf {u}$
is a pole for A. The observation that some sets are convex with respect to a pole was made by Pólya and Szegö (see pages 53–56 in [Reference Pólya and Szegö8, Chapter 2]), but to our knowledge, it was not further developed.
Initial results about polar convexity in the complex plane can be found in [Reference Sendov, Sendov and Wang11], [Reference Sendov and Sendov12]. The motivation for developing a theory of polar convexity comes from the observation that polar convex sets can give refinements of classical results about the location of critical points of polynomials, see for example [Reference Rahman and Schmeisser9]. For example, in [Reference Sendov, Sendov and Wang11], polar convexity was used to give a refinement of the following classical result by Laguerre: Let
![]() $p(z)$
be a polynomial of degree
$p(z)$
be a polynomial of degree
![]() $n\geq 2$
and let
$n\geq 2$
and let
![]() $u \in \mathbb {C}$
. A circular domain containing the zeros of
$u \in \mathbb {C}$
. A circular domain containing the zeros of
![]() $p(z)$
, but not the point u, contains all zeros of the polar derivative of
$p(z)$
, but not the point u, contains all zeros of the polar derivative of
![]() $p(z)$
with respect to u.
$p(z)$
with respect to u.
In [Reference Sendov13], polar convexity was used to give a refinement of the Gauss-Lucas theorem, stating that the critical points of a polynomial are in the convex hull of its zeros. In particular, [Reference Sendov13] shows that the critical points of a polynomial of degree n lie in the intersection of
![]() $n+1$
polar convex hulls, one of them being the usual convex hull of the zeros. In addition, this refines a much older result of Specht [Reference Specht14]. This paper aims to extend these tools and notions to finite-dimensional Euclidean spaces. This allows us to see polar convexity as a natural extension of the classical convex analysis. It is certain that classical convex analysis has revolutionized mathematics, finding applications in areas such as differential equations [Reference Hörmander7], geometry [Reference Cox, Little and Schneck4], optimization [Reference Rockafellar10], matrix analysis [Reference Hoffman and Kunze6], economics [Reference Debreu5] [Reference Mas-Colell, Whinston and Green3], and many more. The hope is to see polar convexity grow in the future and find its niches. While this paper focuses on developing the initial results in the theory of polar convexity, in a subsequent paper, we will show how polar convexity has a deep connection with the critical points and polar derivatives of multivariate polynomials.
$n+1$
polar convex hulls, one of them being the usual convex hull of the zeros. In addition, this refines a much older result of Specht [Reference Specht14]. This paper aims to extend these tools and notions to finite-dimensional Euclidean spaces. This allows us to see polar convexity as a natural extension of the classical convex analysis. It is certain that classical convex analysis has revolutionized mathematics, finding applications in areas such as differential equations [Reference Hörmander7], geometry [Reference Cox, Little and Schneck4], optimization [Reference Rockafellar10], matrix analysis [Reference Hoffman and Kunze6], economics [Reference Debreu5] [Reference Mas-Colell, Whinston and Green3], and many more. The hope is to see polar convexity grow in the future and find its niches. While this paper focuses on developing the initial results in the theory of polar convexity, in a subsequent paper, we will show how polar convexity has a deep connection with the critical points and polar derivatives of multivariate polynomials.
In Section 2, we state the basic definitions and prove some preliminary geometric facts.
In the extended complex plane (see [Reference Sendov, Sendov and Wang11] and [Reference Sendov and Sendov12]), the development of the theory of polar convexity was facilitated by the presence of Möbius transforms. In Section 3, we go over a specific family of Möbius transformations in
![]() $\mathbb {R}^n$
and their special properties that will be important for us. Möbius transformations in
$\mathbb {R}^n$
and their special properties that will be important for us. Möbius transformations in
![]() $\mathbb {R}^n$
have been studied at length over the years, and we refer the reader to [Reference Beardon1, Chapter 3] for a more complete treatment.
$\mathbb {R}^n$
have been studied at length over the years, and we refer the reader to [Reference Beardon1, Chapter 3] for a more complete treatment.
Unlike the classical convexity, polar convexity enjoys a duality property; see Theorem 4.3. In the complex plane, this was proved in [Reference Sendov, Sendov and Wang11], and a very special case of the duality can be found in Problems 107, 112 on pages 54–55 in [Reference Pólya and Szegö8]. In Section 4, we show that the duality holds in finite-dimensional Euclidean spaces, and then we explore its corollaries. As a consequence, we obtain some criteria for checking whether a point is an extreme point for a given polar convex set.
In Section 5, we talk about separation of sets using spherical domains, and we derive polar convex analogues of several classical results of the alternative, such as Gordan’s and Farkas’ lemmas.
In Section 6, we look at sets that are convex with respect to multiple poles. We give a complete characterization for the convex hull of finitely many points with respect to finitely many poles. This allows us to prove some relationships between a set and the set of its poles.
2 Preliminaries and Definitions
For any
![]() $\mathbf {x} \in \mathbb {R}^n \smallsetminus \{\mathbf {0} \}$
, let
$\mathbf {x} \in \mathbb {R}^n \smallsetminus \{\mathbf {0} \}$
, let
This notation is motivated by the fact that
![]() $\langle \mathbf {x} , \mathbf {x}^* \rangle = 1$
and
$\langle \mathbf {x} , \mathbf {x}^* \rangle = 1$
and
![]() $\langle \mathbf {x}^* , \mathbf {x}^* \rangle = 1/\|x\|^2$
, so
$\langle \mathbf {x}^* , \mathbf {x}^* \rangle = 1/\|x\|^2$
, so
![]() $\mathbf {x}^*$
acts like the inverse of the conjugate of a complex number in
$\mathbf {x}^*$
acts like the inverse of the conjugate of a complex number in
![]() $\mathbb {C}$
. We note the easy facts that
$\mathbb {C}$
. We note the easy facts that
With that in mind, we define
 $$ \begin{align*}\mathbf{x}^*:= \left\{\!\!\begin{array}{ll} \infty & \mbox{ if } \mathbf{x}= \mathbf{0}, \\ \mathbf{0} & \mbox{ if } \mathbf{x}=\infty, \end{array} \right. \end{align*} $$
$$ \begin{align*}\mathbf{x}^*:= \left\{\!\!\begin{array}{ll} \infty & \mbox{ if } \mathbf{x}= \mathbf{0}, \\ \mathbf{0} & \mbox{ if } \mathbf{x}=\infty, \end{array} \right. \end{align*} $$
and let
![]() $\hat {\mathbb {R}}^n := \mathbb {R}^n \cup \{\infty \}$
.
$\hat {\mathbb {R}}^n := \mathbb {R}^n \cup \{\infty \}$
.
Definition 2.1 For
![]() $\mathbf {z}_1, \mathbf {z}_2, \mathbf {u} \in \hat {\mathbb {R}}^n$
with
$\mathbf {z}_1, \mathbf {z}_2, \mathbf {u} \in \hat {\mathbb {R}}^n$
with
![]() $\mathbf {z}_1 , \mathbf {z}_2 \neq \mathbf {u}$
, define
$\mathbf {z}_1 , \mathbf {z}_2 \neq \mathbf {u}$
, define
If
![]() $\mathbf {z}_1 = \mathbf {u}$
or
$\mathbf {z}_1 = \mathbf {u}$
or
![]() $\mathbf {z}_2 = \mathbf {u}$
, define
$\mathbf {z}_2 = \mathbf {u}$
, define
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2] := \{\mathbf {z}_1 , \mathbf {z}_2 \}$
.
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1 , \mathbf {z}_2] := \{\mathbf {z}_1 , \mathbf {z}_2 \}$
.
Geometrically, as we will show in Proposition 3.3, this is the arc of the unique circle passing through
![]() $\mathbf {u},\mathbf {z}_1,\mathbf {z}_2$
that lies between
$\mathbf {u},\mathbf {z}_1,\mathbf {z}_2$
that lies between
![]() $\mathbf {z}_1, \mathbf {z}_2$
and does not include
$\mathbf {z}_1, \mathbf {z}_2$
and does not include
![]() $\mathbf {u}$
. For example, if
$\mathbf {u}$
. For example, if
![]() $z_1, z_2, u \in \mathbb {C}$
, then (2.1) simplifies to
$z_1, z_2, u \in \mathbb {C}$
, then (2.1) simplifies to
 $$ \begin{align*}\mathrm{arc}_{u}\left[z_1, z_2 \right] = \Big\{ u + \frac{1}{ \frac{t}{z_1 - u} + \frac{1-t}{ z_2 - u}} : t \in [0,1] \Big\}. \end{align*} $$
$$ \begin{align*}\mathrm{arc}_{u}\left[z_1, z_2 \right] = \Big\{ u + \frac{1}{ \frac{t}{z_1 - u} + \frac{1-t}{ z_2 - u}} : t \in [0,1] \Big\}. \end{align*} $$
Notice that if the points
![]() $\mathbf {z}_1$
,
$\mathbf {z}_1$
,
![]() $\mathbf {z}_2$
, and
$\mathbf {z}_2$
, and
![]() $\mathbf {u}$
are collinear with
$\mathbf {u}$
are collinear with
![]() $\mathbf {u}$
in between
$\mathbf {u}$
in between
![]() $\mathbf {z}_1$
and
$\mathbf {z}_1$
and
![]() $\mathbf {z}_2$
, then there is a
$\mathbf {z}_2$
, then there is a
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
![]() $t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^* = 0$
; that is,
$t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^* = 0$
; that is,
![]() $\infty \in \mathrm {arc}_{\mathbf {u}}\left [ \mathbf {z}_1, \mathbf {z}_2 \right ]$
. If
$\infty \in \mathrm {arc}_{\mathbf {u}}\left [ \mathbf {z}_1, \mathbf {z}_2 \right ]$
. If
![]() $\mathbf {z}_2$
is taken to be
$\mathbf {z}_2$
is taken to be
![]() $\infty $
in (2.1), then
$\infty $
in (2.1), then
This is the ray, starting at
![]() $\mathbf {z}_1$
in the direction of
$\mathbf {z}_1$
in the direction of
![]() $(\mathbf {z}_1 - \mathbf {u})$
with
$(\mathbf {z}_1 - \mathbf {u})$
with
![]() $\infty $
added to the ray.
$\infty $
added to the ray.
The next lemma shows that when
![]() $\|\mathbf {u}\| \rightarrow \infty $
, the arc (2.1) converges to the straight line segment between
$\|\mathbf {u}\| \rightarrow \infty $
, the arc (2.1) converges to the straight line segment between
![]() $\mathbf {z}_1$
and
$\mathbf {z}_1$
and
![]() $\mathbf {z}_2$
. The proof can be found in the appendix.
$\mathbf {z}_2$
. The proof can be found in the appendix.
Lemma 2.1 Given
![]() $\mathbf {u}, \mathbf {z}_1, \mathbf {z}_2 \in \mathbb {R}^n$
and
$\mathbf {u}, \mathbf {z}_1, \mathbf {z}_2 \in \mathbb {R}^n$
and
![]() $t \in [0,1]$
, the point
$t \in [0,1]$
, the point
converges to
![]() $t\mathbf {z}_1 + (1-t)\mathbf {z}_2$
, as
$t\mathbf {z}_1 + (1-t)\mathbf {z}_2$
, as
![]() $\mathbf {u} \rightarrow \infty $
.
$\mathbf {u} \rightarrow \infty $
.
Definition 2.2 Given points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and a
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and a
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the convex hull of
$\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the convex hull of
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to
$\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to
![]() $\mathbf {u}$
to be
$\mathbf {u}$
to be
 $$ \begin{align*}\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1,\ldots , \mathbf{z}_k\} := \Big\{ \mathbf{u} +\big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \big)^* : t_i \geq 0 \text{ with } \sum _{i=1}^k t_i = 1 \Big\}. \end{align*} $$
$$ \begin{align*}\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1,\ldots , \mathbf{z}_k\} := \Big\{ \mathbf{u} +\big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \big)^* : t_i \geq 0 \text{ with } \sum _{i=1}^k t_i = 1 \Big\}. \end{align*} $$
If, say
![]() $\mathbf {z}_1 = \mathbf {u}$
, we define
$\mathbf {z}_1 = \mathbf {u}$
, we define
![]() $\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \} := \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \not =\mathbf {u}, i=1,\ldots , k\} \cup \{ \mathbf {u} \}$
.
$\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \} := \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \not =\mathbf {u}, i=1,\ldots , k\} \cup \{ \mathbf {u} \}$
.
We say that
![]() $\mathbf {u} +\big ( \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^* \big )^*$
is a convex combination of
$\mathbf {u} +\big ( \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^* \big )^*$
is a convex combination of
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to the pole
$\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to the pole
![]() $\mathbf {u}$
or a
$\mathbf {u}$
or a
![]() $\mathbf {u}$
-convex combination for short. A calculation similar to the one in the proof of Lemma 2.1 shows that as we take the limit
$\mathbf {u}$
-convex combination for short. A calculation similar to the one in the proof of Lemma 2.1 shows that as we take the limit
![]() $\mathbf {u} \to \infty $
, the expression
$\mathbf {u} \to \infty $
, the expression
![]() $\mathbf {u} +\big ( \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^* \big )^*$
converges to
$\mathbf {u} +\big ( \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^* \big )^*$
converges to
![]() $\sum _{i=1}^k t_i \mathbf {z}_i$
, the usual convex combination of
$\sum _{i=1}^k t_i \mathbf {z}_i$
, the usual convex combination of
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k$
. Thus, when
$\mathbf {z}_1,\ldots , \mathbf {z}_k$
. Thus, when
![]() $\infty \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, we have
$\infty \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, we have
So, we define
 $$ \begin{align*}\mathrm{conv}_\infty\{ \mathbf{z}_1,\ldots ,\mathbf{z}_k\} := \left\{\!\!\begin{array}{ll} \mathrm{conv}\{ \mathbf{z}_1,\ldots ,\mathbf{z}_k\} & \hspace{-0.2cm} \mbox{ if } \infty \not\in \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}, \\ \mathrm{conv} \{ \mathbf{z}_i : \mathbf{z}_i \not=\infty, i=1,\ldots, k\} \cup \{ \infty \} & \hspace{-0.2cm} \mbox{ if } \infty \in \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}. \end{array} \right. \end{align*} $$
$$ \begin{align*}\mathrm{conv}_\infty\{ \mathbf{z}_1,\ldots ,\mathbf{z}_k\} := \left\{\!\!\begin{array}{ll} \mathrm{conv}\{ \mathbf{z}_1,\ldots ,\mathbf{z}_k\} & \hspace{-0.2cm} \mbox{ if } \infty \not\in \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}, \\ \mathrm{conv} \{ \mathbf{z}_i : \mathbf{z}_i \not=\infty, i=1,\ldots, k\} \cup \{ \infty \} & \hspace{-0.2cm} \mbox{ if } \infty \in \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}. \end{array} \right. \end{align*} $$
The next lemma shows that the set-valued map
![]() $\mathbf {u} \mapsto \mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1,\ldots ,\mathbf {z}_k\}$
has a closed graph.
$\mathbf {u} \mapsto \mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1,\ldots ,\mathbf {z}_k\}$
has a closed graph.
Lemma 2.2 Let
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and let
$\mathbf {z}_1,\ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and let
![]() $\mathbf {u}\in \hat {\mathbb {R}}^n$
be distinct from them. Let
$\mathbf {u}\in \hat {\mathbb {R}}^n$
be distinct from them. Let
![]() $\{\mathbf {u}_m \}$
be a sequence converging to
$\{\mathbf {u}_m \}$
be a sequence converging to
![]() $\mathbf {u}$
. Then, for any sequence
$\mathbf {u}$
. Then, for any sequence
![]() $\mathbf {v}_m \in \mathrm {conv}_{\mathbf {u}_m}\{ z_1,\ldots ,z_k\}$
converging to some
$\mathbf {v}_m \in \mathrm {conv}_{\mathbf {u}_m}\{ z_1,\ldots ,z_k\}$
converging to some
![]() $\mathbf {v}\in \hat {\mathbb {R}}^n$
, we have
$\mathbf {v}\in \hat {\mathbb {R}}^n$
, we have
Conversely, if
![]() $\mathbf {v}\in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots ,\mathbf {z}_k \}$
, then there is a sequence
$\mathbf {v}\in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots ,\mathbf {z}_k \}$
, then there is a sequence
![]() $\{ \mathbf {v}_m\}$
, converging to
$\{ \mathbf {v}_m\}$
, converging to
![]() $\mathbf {v}$
, such that
$\mathbf {v}$
, such that
![]() $\mathbf {v}_m \in \mathrm {conv}_{\mathbf {u}_m} \{ \mathbf {z}_1,\ldots ,\mathbf {z}_k \}$
for every m.
$\mathbf {v}_m \in \mathrm {conv}_{\mathbf {u}_m} \{ \mathbf {z}_1,\ldots ,\mathbf {z}_k \}$
for every m.
Proof Since
![]() $\mathbf {u} \not \in \{\mathbf {z}_1,\ldots , \mathbf {z}_k\}$
and
$\mathbf {u} \not \in \{\mathbf {z}_1,\ldots , \mathbf {z}_k\}$
and
![]() $\{\mathbf {u}_m\}$
converges to
$\{\mathbf {u}_m\}$
converges to
![]() $\mathbf {u}$
, we may assume that
$\mathbf {u}$
, we may assume that
![]() $\mathbf {u}_m \not \in \{\mathbf {z}_1,\ldots , \mathbf {z}_k\}$
for all m. Let
$\mathbf {u}_m \not \in \{\mathbf {z}_1,\ldots , \mathbf {z}_k\}$
for all m. Let
![]() $\mathbf {v}_m = \mathbf {u}_m + \big ( \sum _{i=1}^k t_{m,i} (\mathbf {z}_i - \mathbf {u}_m)^* \big )^*$
for some
$\mathbf {v}_m = \mathbf {u}_m + \big ( \sum _{i=1}^k t_{m,i} (\mathbf {z}_i - \mathbf {u}_m)^* \big )^*$
for some
![]() $t_{m,i} \ge 0$
with
$t_{m,i} \ge 0$
with
![]() $\sum _{i=1}^k t_{m,i} =1$
. Without loss of generality,
$\sum _{i=1}^k t_{m,i} =1$
. Without loss of generality,
![]() $\{t_{m,i}\}_m$
converges to
$\{t_{m,i}\}_m$
converges to
![]() $t_i \ge 0$
, and
$t_i \ge 0$
, and
![]() $\sum _{i=1}^k t_i = 1$
. So we can just take the limit to conclude. The converse is straightforward.
$\sum _{i=1}^k t_i = 1$
. So we can just take the limit to conclude. The converse is straightforward.
Definition 2.3 A set
![]() $A \subseteq \hat {\mathbb {R}}^n$
is said to be convex with respect to
$A \subseteq \hat {\mathbb {R}}^n$
is said to be convex with respect to
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
or
$\mathbf {u} \in \hat {\mathbb {R}}^n$
or
![]() $\mathbf {u}$
-convex if for any
$\mathbf {u}$
-convex if for any
![]() $\mathbf {z}_1, \mathbf {z}_2 \in A$
, we have that
$\mathbf {z}_1, \mathbf {z}_2 \in A$
, we have that
![]() $\mathrm {arc}_{\mathbf {u}}[\mathbf {z}_1, \mathbf {z}_2] \subseteq A$
. For a set
$\mathrm {arc}_{\mathbf {u}}[\mathbf {z}_1, \mathbf {z}_2] \subseteq A$
. For a set
![]() $A \subseteq \hat {\mathbb {R}}^n$
, we define
$A \subseteq \hat {\mathbb {R}}^n$
, we define
![]() $\mathrm {conv}_{\mathbf {u}} (A)$
to be the smallest, with respect to inclusion,
$\mathrm {conv}_{\mathbf {u}} (A)$
to be the smallest, with respect to inclusion,
![]() $\mathbf {u}$
-convex set containing A.
$\mathbf {u}$
-convex set containing A.
Remark 2.3. It is a routine verification similar to the case of usual convexity that
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
as in Definition 2.2 is indeed the smallest
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
as in Definition 2.2 is indeed the smallest
![]() $\mathbf {u}$
-convex set containing
$\mathbf {u}$
-convex set containing
![]() $\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. It should also be clear that intersection of
$\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. It should also be clear that intersection of
![]() $\mathbf {u}$
-convex sets is
$\mathbf {u}$
-convex sets is
![]() $\mathbf {u}$
-convex. In this way,
$\mathbf {u}$
-convex. In this way,
![]() $\mathrm {conv}_{\mathbf {u}} (A)$
is the intersection of all
$\mathrm {conv}_{\mathbf {u}} (A)$
is the intersection of all
![]() $\mathbf {u}$
-convex sets containing A.
$\mathbf {u}$
-convex sets containing A.
Remark 2.4. The reader should note that
![]() $\hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
is always
$\hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
is always
![]() $\mathbf {u}$
-convex for any
$\mathbf {u}$
-convex for any
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
. Now, let
$\mathbf {u} \in \hat {\mathbb {R}}^n$
. Now, let
![]() $A \subseteq \hat {\mathbb {R}}^n$
. If
$A \subseteq \hat {\mathbb {R}}^n$
. If
![]() $\mathbf {u} \not \in A$
, then
$\mathbf {u} \not \in A$
, then
![]() $A \subseteq \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
, and so
$A \subseteq \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
, and so
![]() $\mathrm {conv}_{\mathbf {u}} (A) \subseteq \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
, by the minimality in Definition 2.3 – that is,
$\mathrm {conv}_{\mathbf {u}} (A) \subseteq \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
, by the minimality in Definition 2.3 – that is,
![]() $\mathbf {u} \not \in \mathrm {conv}_{\mathbf {u}} (A)$
. Conversely, if
$\mathbf {u} \not \in \mathrm {conv}_{\mathbf {u}} (A)$
. Conversely, if
![]() $\mathbf {u} \in A$
, then since
$\mathbf {u} \in A$
, then since
![]() $A \subseteq \mathrm {conv}_{\mathbf {u}} (A)$
, we obtain
$A \subseteq \mathrm {conv}_{\mathbf {u}} (A)$
, we obtain
![]() $\mathbf {u} \in \mathrm {conv}_{\mathbf {u}} (A)$
. This shows
$\mathbf {u} \in \mathrm {conv}_{\mathbf {u}} (A)$
. This shows
Similarly, for any
![]() $\mathbf {u}$
-convex set B, the sets
$\mathbf {u}$
-convex set B, the sets
![]() $B \smallsetminus \{ \mathbf {u} \}$
and
$B \smallsetminus \{ \mathbf {u} \}$
and
![]() $B \cup \{ \mathbf {u} \}$
are
$B \cup \{ \mathbf {u} \}$
are
![]() $\mathbf {u}$
-convex.
$\mathbf {u}$
-convex.
Definition 2.4 Given
![]() $A \subseteq \hat {\mathbb {R}}^n$
, we denote by
$A \subseteq \hat {\mathbb {R}}^n$
, we denote by
![]() $\mathcal {P}(A)$
the set of poles of A. That is,
$\mathcal {P}(A)$
the set of poles of A. That is,
![]() $\mathcal {P}(A)$
is the set of all points
$\mathcal {P}(A)$
is the set of all points
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
such that A is
$\mathbf {u} \in \hat {\mathbb {R}}^n$
such that A is
![]() $\mathbf {u}$
-convex.
$\mathbf {u}$
-convex.
Example 2.5. Any closed half-space H is convex with respect to any point not in its interior – that is,
![]() $\mathcal {P}(H) = \mbox {cl}(H^c)$
. Let the closed half-space
$\mathcal {P}(H) = \mbox {cl}(H^c)$
. Let the closed half-space
![]() $H\subset \hat {\mathbb {R}}^n$
be given by
$H\subset \hat {\mathbb {R}}^n$
be given by
![]() $\{ \mathbf {x} \in \mathbb {R}^n : \langle \mathbf {x},\mathbf {v} \rangle \geq c \} \cup \{\infty \}$
for some fixed
$\{ \mathbf {x} \in \mathbb {R}^n : \langle \mathbf {x},\mathbf {v} \rangle \geq c \} \cup \{\infty \}$
for some fixed
![]() $\mathbf {v} \in \mathbb {R}^n$
and
$\mathbf {v} \in \mathbb {R}^n$
and
![]() $c \in \mathbb {R}$
. Without loss of generality, we may assume by translation that
$c \in \mathbb {R}$
. Without loss of generality, we may assume by translation that
![]() $c = 0$
. If
$c = 0$
. If
![]() $\mathbf {u} = \infty $
, there is nothing to show since H is convex in the usual sense. Let
$\mathbf {u} = \infty $
, there is nothing to show since H is convex in the usual sense. Let
![]() $\mathbf {u} \in \mathbb {R}^n$
be such that
$\mathbf {u} \in \mathbb {R}^n$
be such that
![]() $\langle \mathbf {u}, \mathbf {v} \rangle \leq 0$
and let
$\langle \mathbf {u}, \mathbf {v} \rangle \leq 0$
and let
![]() $\mathbf {z}_1, \mathbf {z}_2 \in H$
be distinct. If
$\mathbf {z}_1, \mathbf {z}_2 \in H$
be distinct. If
![]() $\mathbf {z}_2 = \infty $
, then
$\mathbf {z}_2 = \infty $
, then
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \infty ]$
is the ray
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \infty ]$
is the ray
![]() $\{ t\mathbf {z}_1 + (1-t)\mathbf {u} : t \geq 1\}$
, and so
$\{ t\mathbf {z}_1 + (1-t)\mathbf {u} : t \geq 1\}$
, and so
![]() $\langle t\mathbf {z}_1 + (1-t)\mathbf {u} , \mathbf {v} \rangle \geq 0$
. If both
$\langle t\mathbf {z}_1 + (1-t)\mathbf {u} , \mathbf {v} \rangle \geq 0$
. If both
![]() $\mathbf {z}_1, \mathbf {z}_2$
are finite, let
$\mathbf {z}_1, \mathbf {z}_2$
are finite, let
![]() $\mathbf {z} = \mathbf {u} + \big ( t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^* \big )^*$
, where
$\mathbf {z} = \mathbf {u} + \big ( t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^* \big )^*$
, where
![]() $t \in [0,1]$
. Then, because
$t \in [0,1]$
. Then, because
![]() $\langle \mathbf {z}_1 , \mathbf {v} \rangle $
and
$\langle \mathbf {z}_1 , \mathbf {v} \rangle $
and
![]() $\langle \mathbf {z}_2, \mathbf {v} \rangle $
are both nonnegative, we get the following inequality:
$\langle \mathbf {z}_2, \mathbf {v} \rangle $
are both nonnegative, we get the following inequality:
 $$ \begin{align*} \langle \mathbf{z} , \mathbf{v} \rangle &= \langle \mathbf{u} , \mathbf{v} \rangle + \frac{ \langle t (\mathbf{z}_1 - \mathbf{u}), \mathbf{v} \rangle / \|\mathbf{z}_1 - \mathbf{u}\|^2 + \langle (1-t) (\mathbf{z}_2 - \mathbf{u}), \mathbf{v} \rangle /\|\mathbf{z}_2 - \mathbf{u}\|^2 }{\|t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \\ &\geq \langle \mathbf{u} ,\mathbf{v} \rangle \Big( 1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \Big). \end{align*} $$
$$ \begin{align*} \langle \mathbf{z} , \mathbf{v} \rangle &= \langle \mathbf{u} , \mathbf{v} \rangle + \frac{ \langle t (\mathbf{z}_1 - \mathbf{u}), \mathbf{v} \rangle / \|\mathbf{z}_1 - \mathbf{u}\|^2 + \langle (1-t) (\mathbf{z}_2 - \mathbf{u}), \mathbf{v} \rangle /\|\mathbf{z}_2 - \mathbf{u}\|^2 }{\|t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \\ &\geq \langle \mathbf{u} ,\mathbf{v} \rangle \Big( 1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \Big). \end{align*} $$
Since
![]() $\langle \mathbf {u}, \mathbf {v} \rangle \leq 0$
, we need only show that
$\langle \mathbf {u}, \mathbf {v} \rangle \leq 0$
, we need only show that
 $$ \begin{align*}1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \leq 0. \end{align*} $$
$$ \begin{align*}1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \leq 0. \end{align*} $$
This expression, following a similar computation as in the proof of Lemma 2.1, is equal to
 $$ \begin{align*}\frac{-t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 }{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2} \|\mathbf{z}_2 - \mathbf{u}\|^{2}}, \end{align*} $$
$$ \begin{align*}\frac{-t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 }{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2} \|\mathbf{z}_2 - \mathbf{u}\|^{2}}, \end{align*} $$
which is clearly nonpositive. Similarly, one can show that H is not convex with respect to any pole
![]() $\mathbf {u}$
in the interior of H.
$\mathbf {u}$
in the interior of H.
Example 2.6. Consider the positive Lorentz cone, defined by
For all
![]() $\mathbf {v}\in \mathbb {R}^n$
, such that
$\mathbf {v}\in \mathbb {R}^n$
, such that
![]() $\|\mathbf {v}\| =1$
, we have that
$\|\mathbf {v}\| =1$
, we have that
So
That is,
and since
![]() $ L^+ = \bigcap _{\mathbf {v} \in S^{n-1}}H_{\mathbf {v}}^+$
, one sees that equality holds in (2.3). But the right-hand side of (2.3) is just the negative Lorentz cone
$ L^+ = \bigcap _{\mathbf {v} \in S^{n-1}}H_{\mathbf {v}}^+$
, one sees that equality holds in (2.3). But the right-hand side of (2.3) is just the negative Lorentz cone
So we get
![]() $\mathcal {P}(L^+) = L^-$
, and vice-versa by symmetry.
$\mathcal {P}(L^+) = L^-$
, and vice-versa by symmetry.
3 Möbius transformations in
 $\hat {\mathbb {R}}^n$
$\hat {\mathbb {R}}^n$
The general theory of Möbius transformations in
![]() $\hat {\mathbb {R}}^n$
is outside the scope of this paper, and we refer the reader to [Reference Beardon1]. In this section, we quickly review their properties relevant for our purposes. Geometrically, they are defined as finite compositions of reflections in spheres and planes. We have already been using the Möbius transformation
$\hat {\mathbb {R}}^n$
is outside the scope of this paper, and we refer the reader to [Reference Beardon1]. In this section, we quickly review their properties relevant for our purposes. Geometrically, they are defined as finite compositions of reflections in spheres and planes. We have already been using the Möbius transformation
![]() $\mathbf {x} \mapsto \mathbf {x}^*$
, which is the reflection in the unit sphere centered at the origin. Translations and rotations are Möbius transformations. The essential property of the Möbius transformations that allows polar convexity to work in
$\mathbf {x} \mapsto \mathbf {x}^*$
, which is the reflection in the unit sphere centered at the origin. Translations and rotations are Möbius transformations. The essential property of the Möbius transformations that allows polar convexity to work in
![]() $\mathbb {C}$
(see [Reference Sendov, Sendov and Wang11]) is that they send generalized circles to generalized circles. In
$\mathbb {C}$
(see [Reference Sendov, Sendov and Wang11]) is that they send generalized circles to generalized circles. In
![]() $\mathbb {R}^n$
, they send generalized spheres to generalized spheres. The Möbius transformations that are important for this paper are the following family of transformations, indexed by
$\mathbb {R}^n$
, they send generalized spheres to generalized spheres. The Möbius transformations that are important for this paper are the following family of transformations, indexed by
![]() $\mathbf {u} \in \mathbb {R}^n$
:
$\mathbf {u} \in \mathbb {R}^n$
:
 $$ \begin{align*}T_{\mathbf{u}} (\mathbf{z}) := \left\{\!\!\begin{array}{ll} \mathbf{u} + (\mathbf{z}-\mathbf{u})^* & \text{ if } \mathbf{z}\neq \mathbf{u}, \\ \infty &\text{ if } \mathbf{z} = \mathbf{u}, \end{array} \right. \end{align*} $$
$$ \begin{align*}T_{\mathbf{u}} (\mathbf{z}) := \left\{\!\!\begin{array}{ll} \mathbf{u} + (\mathbf{z}-\mathbf{u})^* & \text{ if } \mathbf{z}\neq \mathbf{u}, \\ \infty &\text{ if } \mathbf{z} = \mathbf{u}, \end{array} \right. \end{align*} $$
and let
![]() $T_\infty := \mathrm {Id}_{\hat {\mathbb {R}}^n}.$
Geometrically, these transformations can be described as a reflection in the unit sphere centered at
$T_\infty := \mathrm {Id}_{\hat {\mathbb {R}}^n}.$
Geometrically, these transformations can be described as a reflection in the unit sphere centered at
![]() $\mathbf {u}$
. Note that it is immediate that if
$\mathbf {u}$
. Note that it is immediate that if
![]() $T_{\mathbf {u}} (\mathbf {z})$
is as defined above, then
$T_{\mathbf {u}} (\mathbf {z})$
is as defined above, then
![]() $T_{\mathbf {u}}^2 = \mathrm {Id}_{\hat {\mathbb {R}}^n}$
, and so
$T_{\mathbf {u}}^2 = \mathrm {Id}_{\hat {\mathbb {R}}^n}$
, and so
![]() $T_{\mathbf {u}}$
is an involution. Moreover, it is shown in [Reference Beardon1, Chapter 3] that Möbius transformations are continuous on
$T_{\mathbf {u}}$
is an involution. Moreover, it is shown in [Reference Beardon1, Chapter 3] that Möbius transformations are continuous on
![]() $\hat {\mathbb {R}}^n$
under the chordal metric
$\hat {\mathbb {R}}^n$
under the chordal metric
 $$ \begin{align*}d(\mathbf{x}, \mathbf{y}) := \left\{\!\!\begin{array}{ll} \frac{2|\mathbf{x}-\mathbf{y}|}{(1 + |\mathbf{x}|^2)^{\frac{1}{2}} (1 + |\mathbf{y}|^2)^{\frac{1}{2}}} & \text{ if } \mathbf{x},\mathbf{y} \neq \infty ,\\[0.4cm] \frac{2}{(1 + |\mathbf{x}|^2)^{\frac{1}{2}}} & \text{ if } \mathbf{y} = \infty , \end{array} \right. \end{align*} $$
$$ \begin{align*}d(\mathbf{x}, \mathbf{y}) := \left\{\!\!\begin{array}{ll} \frac{2|\mathbf{x}-\mathbf{y}|}{(1 + |\mathbf{x}|^2)^{\frac{1}{2}} (1 + |\mathbf{y}|^2)^{\frac{1}{2}}} & \text{ if } \mathbf{x},\mathbf{y} \neq \infty ,\\[0.4cm] \frac{2}{(1 + |\mathbf{x}|^2)^{\frac{1}{2}}} & \text{ if } \mathbf{y} = \infty , \end{array} \right. \end{align*} $$
which one gets by using the stereographic projection from
![]() $S^n$
onto
$S^n$
onto
![]() $\hat {\mathbb {R}}^n$
embedded inside
$\hat {\mathbb {R}}^n$
embedded inside
![]() $\hat {\mathbb {R}}^{n+1}$
. The chordal metric restricted to
$\hat {\mathbb {R}}^{n+1}$
. The chordal metric restricted to
![]() $\mathbb {R}^n$
is equivalent to the standard Euclidean metric, and so Möbius transformations are continuous with respect to the standard metric as well. In this work, we refer to the standard metric only and not the chordal metric.
$\mathbb {R}^n$
is equivalent to the standard Euclidean metric, and so Möbius transformations are continuous with respect to the standard metric as well. In this work, we refer to the standard metric only and not the chordal metric.
Definition 3.1 We call any hyperplane in
![]() $\hat {\mathbb {R}}^{n}$
(with
$\hat {\mathbb {R}}^{n}$
(with
![]() $\infty $
included) or any
$\infty $
included) or any
![]() $(n -1)$
-sphere in
$(n -1)$
-sphere in
![]() $\hat {\mathbb {R}}^{n}$
a generalized
$\hat {\mathbb {R}}^{n}$
a generalized
![]() $(n -1)$
-sphere. We call half-spaces in
$(n -1)$
-sphere. We call half-spaces in
![]() $\hat {\mathbb {R}}^{n}$
(with
$\hat {\mathbb {R}}^{n}$
(with
![]() $\infty $
included) and
$\infty $
included) and
![]() $(n -1)$
-spherical domains, open or closed, as generalized
$(n -1)$
-spherical domains, open or closed, as generalized
![]() $(n -1)$
-spherical domains.
$(n -1)$
-spherical domains.
The proof of the next proposition is included for completeness.
Proposition 3.1 The transformation
![]() $T_{\mathbf {u}}$
,
$T_{\mathbf {u}}$
,
![]() $\mathbf {u}\in \hat {\mathbb {R}}^{n}$
, sends a generalized
$\mathbf {u}\in \hat {\mathbb {R}}^{n}$
, sends a generalized
![]() $(n -1)$
-sphere to a generalized
$(n -1)$
-sphere to a generalized
![]() $(n -1)$
-sphere.
$(n -1)$
-sphere.
Proof Translations preserve generalized
![]() $(n -1)$
-spheres, so it is enough to prove that the transformation
$(n -1)$
-spheres, so it is enough to prove that the transformation
![]() $T_{\mathbf {0}} : \mathbf {x} \mapsto \mathbf {x}^*$
preserves them. Any generalized
$T_{\mathbf {0}} : \mathbf {x} \mapsto \mathbf {x}^*$
preserves them. Any generalized
![]() $(n -1 )$
-sphere in
$(n -1 )$
-sphere in
![]() $\hat {\mathbb {R}}^{n}$
is the set of points that satisfy the equation
$\hat {\mathbb {R}}^{n}$
is the set of points that satisfy the equation
for some parameters
![]() $\alpha , \beta \in \mathbb {R}$
and
$\alpha , \beta \in \mathbb {R}$
and
![]() $\mathbf {a} \in \mathbb {R}^{n}$
. By convention,
$\mathbf {a} \in \mathbb {R}^{n}$
. By convention,
![]() $\infty $
satisfies this equation if and only if
$\infty $
satisfies this equation if and only if
![]() $\alpha = 0$
, and then the set is a hyperplane. When
$\alpha = 0$
, and then the set is a hyperplane. When
![]() $\mathbf {x} \neq \mathbf {0}$
, dividing throughout by
$\mathbf {x} \neq \mathbf {0}$
, dividing throughout by
![]() $\| \mathbf {x} \|^2$
, we get
$\| \mathbf {x} \|^2$
, we get
and this is the equation of the image of (3.1) under
![]() $T_{\mathbf {0}}$
. If
$T_{\mathbf {0}}$
. If
![]() $\mathbf {0}$
satisfies the original equation, then
$\mathbf {0}$
satisfies the original equation, then
![]() $\beta = 0$
, and (3.2) reduces to an equation of a hyperplane. In that case,
$\beta = 0$
, and (3.2) reduces to an equation of a hyperplane. In that case,
![]() $\infty $
also satisfies that equation.
$\infty $
also satisfies that equation.
Definition 3.2 We call any k-dimensional affine subspace of
![]() $\hat {\mathbb {R}}^n$
(with
$\hat {\mathbb {R}}^n$
(with
![]() $\infty $
included) or any k dimensional sphere (the intersection of a
$\infty $
included) or any k dimensional sphere (the intersection of a
![]() $(k+1)$
-dimensional affine subspace with an
$(k+1)$
-dimensional affine subspace with an
![]() $(n -1)$
-sphere) in
$(n -1)$
-sphere) in
![]() $\hat {\mathbb {R}}^{n}$
a generalized k-sphere.
$\hat {\mathbb {R}}^{n}$
a generalized k-sphere.
Proposition 3.2 The transformation
![]() $T_{\mathbf {u}}$
,
$T_{\mathbf {u}}$
,
![]() $\mathbf {u} \in \hat {\mathbb {R}}^{n}$
, sends a generalized k-sphere to a generalized k-sphere.
$\mathbf {u} \in \hat {\mathbb {R}}^{n}$
, sends a generalized k-sphere to a generalized k-sphere.
Proof Any k-sphere in
![]() $\hat {\mathbb {R}}^{n}$
can be written as an intersection of a
$\hat {\mathbb {R}}^{n}$
can be written as an intersection of a
![]() $(n-1)$
-sphere with
$(n-1)$
-sphere with
![]() $n - k -1$
distinct hyperplanes. Since
$n - k -1$
distinct hyperplanes. Since
![]() $T_{\mathbf {u}}$
is bijective, these are sent to distinct hyperplanes and
$T_{\mathbf {u}}$
is bijective, these are sent to distinct hyperplanes and
![]() $(n -1)$
-spheres, and they intersect in a k-sphere.
$(n -1)$
-spheres, and they intersect in a k-sphere.
Specifically, this says that
![]() $T_{\mathbf {u}}$
sends generalized circles to generalized circles, and any circle passing through
$T_{\mathbf {u}}$
sends generalized circles to generalized circles, and any circle passing through
![]() $\mathbf {u}$
, since
$\mathbf {u}$
, since
![]() $T_{\mathbf {u}}$
sends
$T_{\mathbf {u}}$
sends
![]() $\mathbf {u}$
to
$\mathbf {u}$
to
![]() $\infty $
, is mapped to a line.
$\infty $
, is mapped to a line.
Proposition 3.3 For
![]() $\mathbf {z}_1, \mathbf {z}_2, \mathbf {u} \in \hat {\mathbb {R}}^n$
with
$\mathbf {z}_1, \mathbf {z}_2, \mathbf {u} \in \hat {\mathbb {R}}^n$
with
![]() $\mathbf {z}_1 , \mathbf {z}_2 \neq \mathbf {u}$
, the set
$\mathbf {z}_1 , \mathbf {z}_2 \neq \mathbf {u}$
, the set
![]() $\mathrm {arc}_{\mathbf {u}}\left [ \mathbf {z}_1, \mathbf {z}_2 \right ]$
is the arc of the unique circle passing through
$\mathrm {arc}_{\mathbf {u}}\left [ \mathbf {z}_1, \mathbf {z}_2 \right ]$
is the arc of the unique circle passing through
![]() $\mathbf {u},\mathbf {z}_1,\mathbf {z}_2$
that lies between
$\mathbf {u},\mathbf {z}_1,\mathbf {z}_2$
that lies between
![]() $\mathbf {z}_1, \mathbf {z}_2$
and does not include
$\mathbf {z}_1, \mathbf {z}_2$
and does not include
![]() $\mathbf {u}$
.
$\mathbf {u}$
.
Proof The Möbius transformation
![]() $T_{\mathbf {u}}$
sends the circle through
$T_{\mathbf {u}}$
sends the circle through
![]() $\mathbf {u}, \mathbf {z}_1, \mathbf {z}_2$
to the line through
$\mathbf {u}, \mathbf {z}_1, \mathbf {z}_2$
to the line through
![]() $\infty , T_{\mathbf {u}}(\mathbf {z}_1), T_{\mathbf {u}}(\mathbf {z}_2)$
. The arc of the circle lying between
$\infty , T_{\mathbf {u}}(\mathbf {z}_1), T_{\mathbf {u}}(\mathbf {z}_2)$
. The arc of the circle lying between
![]() $\mathbf {z}_1, \mathbf {z}_2$
that does not include
$\mathbf {z}_1, \mathbf {z}_2$
that does not include
![]() $\mathbf {u}$
gets sent to the segment between
$\mathbf {u}$
gets sent to the segment between
![]() $T_{\mathbf {u}}(\mathbf {z}_1)$
and
$T_{\mathbf {u}}(\mathbf {z}_1)$
and
![]() $T_{\mathbf {u}}(\mathbf {z}_2)$
not containing
$T_{\mathbf {u}}(\mathbf {z}_2)$
not containing
![]() $\infty $
. Taking the inverse image of the points on this segment, the points on the arc can be written as
$\infty $
. Taking the inverse image of the points on this segment, the points on the arc can be written as
![]() $T_{\mathbf {u}} (tT_{\mathbf {u}}(\mathbf {z}_1) + (1-t) T_{\mathbf {u}}(\mathbf {z}_2) )$
for
$T_{\mathbf {u}} (tT_{\mathbf {u}}(\mathbf {z}_1) + (1-t) T_{\mathbf {u}}(\mathbf {z}_2) )$
for
![]() $0 \leq t \leq 1$
, which is exactly the parametrization in Definition 2.1.
$0 \leq t \leq 1$
, which is exactly the parametrization in Definition 2.1.
Proposition 3.4 The transformation
![]() $T_{\mathbf {u}}$
,
$T_{\mathbf {u}}$
,
![]() $\mathbf {u} \in \hat {\mathbb {R}}^{n}$
, sends
$\mathbf {u} \in \hat {\mathbb {R}}^{n}$
, sends
![]() $\mathbf {u}$
-convex sets to convex sets and convex sets to
$\mathbf {u}$
-convex sets to convex sets and convex sets to
![]() $\mathbf {u}$
-convex sets.
$\mathbf {u}$
-convex sets.
Proof Let S be a
![]() $\mathbf {u}$
-convex set and
$\mathbf {u}$
-convex set and
![]() $\mathbf {z}_1, \mathbf {z}_2 \in S$
. Since
$\mathbf {z}_1, \mathbf {z}_2 \in S$
. Since
![]() $T_{\mathbf {u}}$
sends
$T_{\mathbf {u}}$
sends
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \mathbf {z}_2]$
to the line segment
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \mathbf {z}_2]$
to the line segment
![]() $\{ t T_{\mathbf {u}} (\mathbf {z}_1) + (1-t)T_{\mathbf {u}} (\mathbf {z}_2) : t \in [0,1] \}$
, we see that it is in
$\{ t T_{\mathbf {u}} (\mathbf {z}_1) + (1-t)T_{\mathbf {u}} (\mathbf {z}_2) : t \in [0,1] \}$
, we see that it is in
![]() $T_{\mathbf {u}}(S)$
. As
$T_{\mathbf {u}}(S)$
. As
![]() $T_{\mathbf {u}}$
is a bijection, we see that the segment between any pair of points from
$T_{\mathbf {u}}$
is a bijection, we see that the segment between any pair of points from
![]() $T_{\mathbf {u}} (S)$
is in
$T_{\mathbf {u}} (S)$
is in
![]() $T_{\mathbf {u}} (S)$
, so it is convex. A similar argument shows the other half of the lemma.
$T_{\mathbf {u}} (S)$
, so it is convex. A similar argument shows the other half of the lemma.
Definition 3.3 Let
![]() $S \subset \hat {\mathbb {R}}^n$
be a sphere. We call a subset
$S \subset \hat {\mathbb {R}}^n$
be a sphere. We call a subset
![]() $S' \subset S$
, a spherical domain in S if
$S' \subset S$
, a spherical domain in S if
![]() $S' = S \cap S"$
for some spherical domain
$S' = S \cap S"$
for some spherical domain
![]() $S"$
in
$S"$
in
![]() $\hat {\mathbb {R}}^n$
. Equivalently,
$\hat {\mathbb {R}}^n$
. Equivalently,
![]() $S'\subset S$
is a spherical domain in S if for some point
$S'\subset S$
is a spherical domain in S if for some point
![]() $\mathbf {u} \in S$
,
$\mathbf {u} \in S$
,
![]() $T_{\mathbf {u}} (S')$
is a spherical domain in the affine space
$T_{\mathbf {u}} (S')$
is a spherical domain in the affine space
![]() $T_{\mathbf {u}} (S)$
.
$T_{\mathbf {u}} (S)$
.
Remark 3.5. For any set
![]() $A\subseteq \hat {\mathbb {R}}^n$
, both
$A\subseteq \hat {\mathbb {R}}^n$
, both
![]() $\mathrm {conv}_{\mathbf {u}} (A)$
and
$\mathrm {conv}_{\mathbf {u}} (A)$
and
![]() $\mathrm {conv}(T_{\mathbf {u}} (A))$
are minimal sets among the family of
$\mathrm {conv}(T_{\mathbf {u}} (A))$
are minimal sets among the family of
![]() $\mathbf {u}$
-convex sets and convex sets, containing A and
$\mathbf {u}$
-convex sets and convex sets, containing A and
![]() $T_{\mathbf {u}} (A)$
, respectively. Since
$T_{\mathbf {u}} (A)$
, respectively. Since
![]() $T_{\mathbf {u}}$
sends one family to the other, as a consequence of the last proposition, we get that
$T_{\mathbf {u}}$
sends one family to the other, as a consequence of the last proposition, we get that
So, in particular, we have
A consequence of this fact is the observation that if
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
are distinct points in
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
are distinct points in
![]() $\hat {\mathbb {R}}^n$
, then
$\hat {\mathbb {R}}^n$
, then
![]() $\mathbf {u} \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}.$
Indeed, just note that
$\mathbf {u} \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}.$
Indeed, just note that
since all of the points
![]() $T_{\mathbf {u}} (\mathbf {z}_i)$
,
$T_{\mathbf {u}} (\mathbf {z}_i)$
,
![]() $i=1,\ldots , k$
, are finite.
$i=1,\ldots , k$
, are finite.
Example 3.6. Referring back to Example 2.5, we can now see that including the point
![]() $\infty $
in H is crucial. Because if
$\infty $
in H is crucial. Because if
![]() $\mathbf {u} \neq \infty $
were on the boundary of the half-space H, then
$\mathbf {u} \neq \infty $
were on the boundary of the half-space H, then
![]() $T_{\mathbf {u}} (H \smallsetminus \{ \infty \})$
is a half-space with one point on the boundary missing, so it cannot be convex.
$T_{\mathbf {u}} (H \smallsetminus \{ \infty \})$
is a half-space with one point on the boundary missing, so it cannot be convex.
However, if
![]() $\mathbf {u} \in H^c$
, then
$\mathbf {u} \in H^c$
, then
![]() $T_{\mathbf {u}} (H \smallsetminus \{ \infty \})$
is a closed sphere with one point (i.e.,
$T_{\mathbf {u}} (H \smallsetminus \{ \infty \})$
is a closed sphere with one point (i.e.,
![]() $\mathbf {u}$
) on the boundary missing, which happens to be convex, so
$\mathbf {u}$
) on the boundary missing, which happens to be convex, so
![]() $H \smallsetminus \{ \infty \}$
is convex with respect to any pole in
$H \smallsetminus \{ \infty \}$
is convex with respect to any pole in
![]() $\hat {\mathbb {R}}^n \smallsetminus H$
.
$\hat {\mathbb {R}}^n \smallsetminus H$
.
Example 3.7. Any open half-space is convex with respect to any point not in it. Let the open half-space
![]() $H \subset \hat {\mathbb {R}}^n$
be given by
$H \subset \hat {\mathbb {R}}^n$
be given by
for some fixed
![]() $\mathbf {v} \in \mathbb {R}^n$
and
$\mathbf {v} \in \mathbb {R}^n$
and
![]() $c\in \mathbb {R}$
, and let
$c\in \mathbb {R}$
, and let
![]() $\mathbf {u} \not \in H$
be any point. The fact is simple if
$\mathbf {u} \not \in H$
be any point. The fact is simple if
![]() $\mathbf {u} = \infty $
. If
$\mathbf {u} = \infty $
. If
![]() $\langle \mathbf {u} , \mathbf {v} \rangle =0$
, then
$\langle \mathbf {u} , \mathbf {v} \rangle =0$
, then
![]() $T_{\mathbf {u}} (H)$
is an open half-space and so it is convex as
$T_{\mathbf {u}} (H)$
is an open half-space and so it is convex as
![]() $T_{\mathbf {u}}$
maps the boundary hyperplane
$T_{\mathbf {u}}$
maps the boundary hyperplane
![]() $\partial H : = \{\mathbf {x} \in \hat {\mathbb {R}}^n : \langle \mathbf {x} , \mathbf {v} \rangle = 0 \} \cup \{ \infty \}$
to a hyperplane. In a similar fashion, if
$\partial H : = \{\mathbf {x} \in \hat {\mathbb {R}}^n : \langle \mathbf {x} , \mathbf {v} \rangle = 0 \} \cup \{ \infty \}$
to a hyperplane. In a similar fashion, if
![]() $\langle \mathbf {u} , \mathbf {v} \rangle < 0$
, then
$\langle \mathbf {u} , \mathbf {v} \rangle < 0$
, then
![]() $\mathbf {u} \not \in \partial H$
. Thus,
$\mathbf {u} \not \in \partial H$
. Thus,
![]() $T_{\mathbf {u}}$
maps the hyperplane
$T_{\mathbf {u}}$
maps the hyperplane
![]() $\partial H$
to a proper sphere. Since
$\partial H$
to a proper sphere. Since
![]() $T_{\mathbf {u}} (\mathbf {u}) = \infty \not \in T_{\mathbf {u}}(H)$
, we get that
$T_{\mathbf {u}} (\mathbf {u}) = \infty \not \in T_{\mathbf {u}}(H)$
, we get that
![]() $T_{\mathbf {u}} (H)$
is the bounded open sphere and is thus convex. Therefore, the open half-space H is
$T_{\mathbf {u}} (H)$
is the bounded open sphere and is thus convex. Therefore, the open half-space H is
![]() $\mathbf {u}$
-convex for any
$\mathbf {u}$
-convex for any
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n \smallsetminus H$
.
$\mathbf {u} \in \hat {\mathbb {R}}^n \smallsetminus H$
.
Example 3.8. We show that a spherical domain
![]() $S \subseteq \hat {\mathbb {R}}^n$
(open or closed) is convex with respect to any point
$S \subseteq \hat {\mathbb {R}}^n$
(open or closed) is convex with respect to any point
![]() $\mathbf {u} \in \mathrm {cl}(S^c)$
. The cases when S is an open or closed half-space have been discussed in Examples 2.5 and 3.7. If
$\mathbf {u} \in \mathrm {cl}(S^c)$
. The cases when S is an open or closed half-space have been discussed in Examples 2.5 and 3.7. If
![]() $\mathbf {u}$
lies in
$\mathbf {u}$
lies in
![]() $\partial {S}$
, then
$\partial {S}$
, then
![]() $T_{\mathbf {u}} (\partial {S} )$
is a hyperplane. So,
$T_{\mathbf {u}} (\partial {S} )$
is a hyperplane. So,
![]() $T_{\mathbf {u}} (S)$
is a half-space and is therefore convex. If
$T_{\mathbf {u}} (S)$
is a half-space and is therefore convex. If
![]() $\mathbf {u}$
is in
$\mathbf {u}$
is in
![]() $(\mbox {cl} S)^c$
, then
$(\mbox {cl} S)^c$
, then
![]() $T_{\mathbf {u}} (\partial {S})$
is a proper sphere. Since
$T_{\mathbf {u}} (\partial {S})$
is a proper sphere. Since
![]() $\mathbf {u} \not \in S$
,
$\mathbf {u} \not \in S$
,
![]() $T_{\mathbf {u}} (S)$
is the (open or closed) bounded component of
$T_{\mathbf {u}} (S)$
is the (open or closed) bounded component of
![]() $\hat {\mathbb {R}}^n \smallsetminus T_{\mathbf {u}} (\partial {S})$
. From this, we can conclude that
$\hat {\mathbb {R}}^n \smallsetminus T_{\mathbf {u}} (\partial {S})$
. From this, we can conclude that
![]() $T_{\mathbf {u}} (S)$
is convex, and hence, S is
$T_{\mathbf {u}} (S)$
is convex, and hence, S is
![]() $\mathbf {u}$
-convex. In other words, for a spherical domain S, we have
$\mathbf {u}$
-convex. In other words, for a spherical domain S, we have
![]() $\mathcal {P}(S) = \mbox {cl}(S^c)$
.
$\mathcal {P}(S) = \mbox {cl}(S^c)$
.
From now on, the word generalized (in generalized spherical domains) will be dropped, and when talking of spherical domains, it will be assumed that we mean spherical domains of real co-dimension one unless otherwise stated.
Often in situations where we deal with a single pole
![]() $\mathbf {u}$
, we may use the transform
$\mathbf {u}$
, we may use the transform
![]() $T_{\mathbf {u}}$
to send
$T_{\mathbf {u}}$
to send
![]() $\mathbf {u}$
to
$\mathbf {u}$
to
![]() $\infty $
and translate the problem to one in the realm of classical convexity.
$\infty $
and translate the problem to one in the realm of classical convexity.
4 A duality theorem
The goal of this section is to prove the “duality” Theorem 4.3, which gives us a duality between poles and points in the polar convex hull. Before we state it, we record some computational results that will aid us in the proof of the theorem.
Lemma 4.1 Let
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, and let
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, and let
 $$ \begin{align*}\mathbf{v} = \mathbf{u} + \Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big)^*, \end{align*} $$
$$ \begin{align*}\mathbf{v} = \mathbf{u} + \Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big)^*, \end{align*} $$
for some
![]() $t_i \ge 0$
,
$t_i \ge 0$
,
![]() $1\leq i \leq k$
, such that
$1\leq i \leq k$
, such that
![]() $\sum _{i=1}^k t_i = 1$
. Then, we have the following relationships:
$\sum _{i=1}^k t_i = 1$
. Then, we have the following relationships:
-
(a)
 $\|\mathbf {v} -\mathbf {u} \|=\|\sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^*\|^{-1};$
$\|\mathbf {v} -\mathbf {u} \|=\|\sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^*\|^{-1};$
-
(b)
 $( \mathbf {v} - \mathbf {u} )^* = \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^*;$
and
$( \mathbf {v} - \mathbf {u} )^* = \sum _{i=1}^k t_i (\mathbf {z}_i - \mathbf {u})^*;$
and -
(c)
 $\sum _{i=1}^k t_i \frac {\|\mathbf {z}_i - \mathbf {v}\|^2}{\|\mathbf {z}_i - \mathbf {u}\|^2} = \sum _{i=1}^k t_i\frac {\|\mathbf {v} - \mathbf {u} \|^2}{\|\mathbf {z}_i - \mathbf {u}\|^2} -1.$
$\sum _{i=1}^k t_i \frac {\|\mathbf {z}_i - \mathbf {v}\|^2}{\|\mathbf {z}_i - \mathbf {u}\|^2} = \sum _{i=1}^k t_i\frac {\|\mathbf {v} - \mathbf {u} \|^2}{\|\mathbf {z}_i - \mathbf {u}\|^2} -1.$
Proof
-
(a) This part is straightforward:
 $$ \begin{align*} \|\mathbf{v} -\mathbf{u} \| &= \Big\| \Big(\sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u} )^*\Big)^* \Big\| =\Big \|\sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big\|^{-1}. \end{align*} $$
$$ \begin{align*} \|\mathbf{v} -\mathbf{u} \| &= \Big\| \Big(\sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u} )^*\Big)^* \Big\| =\Big \|\sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big\|^{-1}. \end{align*} $$
-
(b) This follows trivially from the fact that
 $(\mathbf {x}^*)^* = \mathbf {x}$
.
$(\mathbf {x}^*)^* = \mathbf {x}$
. -
(c) We can rewrite the stated expression as
Then, we expand the part in the parentheses in the numerator of each summand: $$ \begin{align*}0 = \sum _{i=1}^k \frac{t_i ( \|\mathbf{v} -\mathbf{u} \|^2 -\|\mathbf{z}_i - \mathbf{u}\|^2 - \|\mathbf{z}_i - \mathbf{v} \|^2)}{\|\mathbf{z}_i - \mathbf{u} \|^2}. \end{align*} $$
Multiply the last expression by
$$ \begin{align*}0 = \sum _{i=1}^k \frac{t_i ( \|\mathbf{v} -\mathbf{u} \|^2 -\|\mathbf{z}_i - \mathbf{u}\|^2 - \|\mathbf{z}_i - \mathbf{v} \|^2)}{\|\mathbf{z}_i - \mathbf{u} \|^2}. \end{align*} $$
Multiply the last expression by $$ \begin{align*} \|\mathbf{v} - &\mathbf{u} \|^2 - \|\mathbf{z}_i - \mathbf{u} \|^2 - \|\mathbf{z}_i - \mathbf{v}\|^2\\ &= (\langle \mathbf{v}, \mathbf{v} \rangle - \langle \mathbf{v},\mathbf{u} \rangle - \langle \mathbf{u},\mathbf{v} \rangle + \langle \mathbf{u},\mathbf{u} \rangle) - (\langle \mathbf{z}_i , \mathbf{z}_i \rangle - \langle \mathbf{z}_i, \mathbf{u} \rangle - \langle \mathbf{u}, \mathbf{z}_i \rangle + \langle \mathbf{u},\mathbf{u} \rangle) \\ & \hspace{5.6cm} - (\langle \mathbf{z}_i , \mathbf{z}_i \rangle - \langle \mathbf{z}_i,\mathbf{v} \rangle - \langle \mathbf{v}, \mathbf{z}_i \rangle + \langle \mathbf{v} ,\mathbf{v} \rangle) \\ &= - \langle \mathbf{v},\mathbf{u} \rangle - \langle \mathbf{u},\mathbf{v} \rangle - \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i, \mathbf{u} \rangle + \langle \mathbf{u}, \mathbf{z}_i \rangle - \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i,\mathbf{v} \rangle + \langle \mathbf{v}, \mathbf{z}_i \rangle \\ &= \langle \mathbf{v} - \mathbf{u} , \mathbf{z}_i - \mathbf{u} \rangle + \langle \mathbf{z}_i - \mathbf{u} , \mathbf{v} - \mathbf{u} \rangle - 2 \langle \mathbf{z}_i - \mathbf{u} , \mathbf{z}_i - \mathbf{u} \rangle. \end{align*} $$
$$ \begin{align*} \|\mathbf{v} - &\mathbf{u} \|^2 - \|\mathbf{z}_i - \mathbf{u} \|^2 - \|\mathbf{z}_i - \mathbf{v}\|^2\\ &= (\langle \mathbf{v}, \mathbf{v} \rangle - \langle \mathbf{v},\mathbf{u} \rangle - \langle \mathbf{u},\mathbf{v} \rangle + \langle \mathbf{u},\mathbf{u} \rangle) - (\langle \mathbf{z}_i , \mathbf{z}_i \rangle - \langle \mathbf{z}_i, \mathbf{u} \rangle - \langle \mathbf{u}, \mathbf{z}_i \rangle + \langle \mathbf{u},\mathbf{u} \rangle) \\ & \hspace{5.6cm} - (\langle \mathbf{z}_i , \mathbf{z}_i \rangle - \langle \mathbf{z}_i,\mathbf{v} \rangle - \langle \mathbf{v}, \mathbf{z}_i \rangle + \langle \mathbf{v} ,\mathbf{v} \rangle) \\ &= - \langle \mathbf{v},\mathbf{u} \rangle - \langle \mathbf{u},\mathbf{v} \rangle - \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i, \mathbf{u} \rangle + \langle \mathbf{u}, \mathbf{z}_i \rangle - \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i,\mathbf{v} \rangle + \langle \mathbf{v}, \mathbf{z}_i \rangle \\ &= \langle \mathbf{v} - \mathbf{u} , \mathbf{z}_i - \mathbf{u} \rangle + \langle \mathbf{z}_i - \mathbf{u} , \mathbf{v} - \mathbf{u} \rangle - 2 \langle \mathbf{z}_i - \mathbf{u} , \mathbf{z}_i - \mathbf{u} \rangle. \end{align*} $$
 $t_i$
and divide it by
$t_i$
and divide it by
 $\|\mathbf {z}_i - \mathbf {u} \|^2$
. Then, sum over i from
$\|\mathbf {z}_i - \mathbf {u} \|^2$
. Then, sum over i from
 $1$
to k and use part (b) of the current lemma to obtain
$1$
to k and use part (b) of the current lemma to obtain  $$ \begin{align*} \Big\langle \mathbf{v} -\mathbf{u} , \sum _{i=1}^k t_i \frac{ \mathbf{z}_i - \mathbf{u} }{\|\mathbf{z}_i - \mathbf{u} \|^2} \Big\rangle &+\Big\langle \sum _{i=1}^k t_i\frac{ \mathbf{z}_i - \mathbf{u} }{\|\mathbf{z}_i - \mathbf{u} \|^2}, \mathbf{v} -\mathbf{u} \Big\rangle -2 \\ &= \langle \mathbf{v} -\mathbf{u} , (\mathbf{v} -\mathbf{u})^* \rangle +\langle (\mathbf{v} -\mathbf{u})^*, \mathbf{v} -\mathbf{u} \rangle -2 \\ &=0. \end{align*} $$
$$ \begin{align*} \Big\langle \mathbf{v} -\mathbf{u} , \sum _{i=1}^k t_i \frac{ \mathbf{z}_i - \mathbf{u} }{\|\mathbf{z}_i - \mathbf{u} \|^2} \Big\rangle &+\Big\langle \sum _{i=1}^k t_i\frac{ \mathbf{z}_i - \mathbf{u} }{\|\mathbf{z}_i - \mathbf{u} \|^2}, \mathbf{v} -\mathbf{u} \Big\rangle -2 \\ &= \langle \mathbf{v} -\mathbf{u} , (\mathbf{v} -\mathbf{u})^* \rangle +\langle (\mathbf{v} -\mathbf{u})^*, \mathbf{v} -\mathbf{u} \rangle -2 \\ &=0. \end{align*} $$
This completes the proof.
Part (c) of the last lemma is often helpful in simplifying computations, as demonstrated by the following example.
Example 4.2. It is well-known that the convex cone
![]() $S^n_+$
of
$S^n_+$
of
![]() $n \times n$
positive semi-definite matrices is a convex cone. We show here that it is also polar convex with respect to any matrix in the negative semi-definite cone
$n \times n$
positive semi-definite matrices is a convex cone. We show here that it is also polar convex with respect to any matrix in the negative semi-definite cone
![]() $S^n_-$
. To see this, take
$S^n_-$
. To see this, take
![]() $U \in S^n_-$
and
$U \in S^n_-$
and
![]() $A_1, A_2 \in S^n_+$
. Then, for any
$A_1, A_2 \in S^n_+$
. Then, for any
![]() $t \in [0,1]$
, let
$t \in [0,1]$
, let
We show that A is a positive semi-definite matrix. Indeed, by Lemma 4.1, part (a), we have
 $$ \begin{align*} A &= U + \frac{ t (A_1 - U)^* + (1-t) (A_2 - U)^*}{\| t (A_1 - U)^* + (1-t) (A_2 - U)^* \|^2} \\ &= U + (t (A_1 - U)^* + (1-t) (A_2 - U)^*) \|A -U\|^2\\ &= U + \Big(t \frac{A_1 - U}{\| A_1 - U \|^2} + (1-t) \frac{A_2 - U }{\| A_2 - U \|^2}\Big) \|A -U\|^2\\ &= U \Big( 1 - t\frac{ \|A - U\|^2}{\|A_1 - U\|^2} - (1-t)\frac{ \|A - U\|^2}{\|A_2 - U\|^2} \Big) \\ & \hspace{0.7cm} + A_1 t \frac{ \|A-U\|^2}{\|A_1 - U\|^2} + A_2 (1-t) \frac{\|A-U\|^2 }{\|A_2 - U\|^2} \\ &= - U \Big( t\frac{ \|A_1 - A\|^2}{\|A_1 - U\|^2} + (1-t)\frac{ \|A_2 - A\|^2}{\|A_2 - U\|^2} \Big) \\ & \hspace{0.7cm} + A_1 t \frac{ \|A-U\|^2}{\|A_1 - U\|^2} + A_2 (1-t) \frac{\|A-U\|^2 }{\|A_2 - U\|^2} \geq 0, \end{align*} $$
$$ \begin{align*} A &= U + \frac{ t (A_1 - U)^* + (1-t) (A_2 - U)^*}{\| t (A_1 - U)^* + (1-t) (A_2 - U)^* \|^2} \\ &= U + (t (A_1 - U)^* + (1-t) (A_2 - U)^*) \|A -U\|^2\\ &= U + \Big(t \frac{A_1 - U}{\| A_1 - U \|^2} + (1-t) \frac{A_2 - U }{\| A_2 - U \|^2}\Big) \|A -U\|^2\\ &= U \Big( 1 - t\frac{ \|A - U\|^2}{\|A_1 - U\|^2} - (1-t)\frac{ \|A - U\|^2}{\|A_2 - U\|^2} \Big) \\ & \hspace{0.7cm} + A_1 t \frac{ \|A-U\|^2}{\|A_1 - U\|^2} + A_2 (1-t) \frac{\|A-U\|^2 }{\|A_2 - U\|^2} \\ &= - U \Big( t\frac{ \|A_1 - A\|^2}{\|A_1 - U\|^2} + (1-t)\frac{ \|A_2 - A\|^2}{\|A_2 - U\|^2} \Big) \\ & \hspace{0.7cm} + A_1 t \frac{ \|A-U\|^2}{\|A_1 - U\|^2} + A_2 (1-t) \frac{\|A-U\|^2 }{\|A_2 - U\|^2} \geq 0, \end{align*} $$
where the last equality follows from Lemma 4.1, part (c). We see that A is a linear combination of positive semi-definite matrices with nonnegative coefficients. Therefore, A is a positive semi-definite matrix.
With these identities proved, we proceed to prove the main result in this section, which gives us a duality between poles and points in the polar convex hull.
Theorem 4.3 (Duality Theorem)
Let
![]() $\mathbf {u} ,\mathbf {v} ,\mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
$\mathbf {u} ,\mathbf {v} ,\mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
![]() $\hat {\mathbb {R}}^n$
. Then,
$\hat {\mathbb {R}}^n$
. Then,
Proof By symmetry, we prove only the necessity. Without loss of generality, we may assume that none of
![]() $\mathbf {u} , \mathbf {v} ,\mathbf {z}_1 , \ldots , \mathbf {z}_k$
are
$\mathbf {u} , \mathbf {v} ,\mathbf {z}_1 , \ldots , \mathbf {z}_k$
are
![]() $\infty $
. (Otherwise, pick a point
$\infty $
. (Otherwise, pick a point
![]() $\mathbf {z} \not \in \{\mathbf {u}, \mathbf {v}, \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, and apply
$\mathbf {z} \not \in \{\mathbf {u}, \mathbf {v}, \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, and apply
![]() $T_{\mathbf {z}}$
.) Let
$T_{\mathbf {z}}$
.) Let
 $$ \begin{align*}\mathbf{v} = \mathbf{u} + \Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* ,\end{align*} $$
$$ \begin{align*}\mathbf{v} = \mathbf{u} + \Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* ,\end{align*} $$
for some
![]() $t_i \ge 0$
,
$t_i \ge 0$
,
![]() $\sum _{i=1}^k t_i =1$
. Observe that
$\sum _{i=1}^k t_i =1$
. Observe that
 $$ \begin{align*} \sum _{i=1}^k t_i \frac{ \mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} &= \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* + t_i \frac{\mathbf{u} - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2}\\ &= (\mathbf{v}-\mathbf{u})^* + \sum _{i=1}^k t_i \frac{\mathbf{u} - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \\ &= ( \mathbf{v} -\mathbf{u} ) \Big( \frac{1}{\|\mathbf{v} - \mathbf{u}\|^{2}} - \sum _{i=1}^k \frac{t_i}{\|\mathbf{z}_i - \mathbf{u}\|^{2}} \Big). \end{align*} $$
$$ \begin{align*} \sum _{i=1}^k t_i \frac{ \mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} &= \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* + t_i \frac{\mathbf{u} - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2}\\ &= (\mathbf{v}-\mathbf{u})^* + \sum _{i=1}^k t_i \frac{\mathbf{u} - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \\ &= ( \mathbf{v} -\mathbf{u} ) \Big( \frac{1}{\|\mathbf{v} - \mathbf{u}\|^{2}} - \sum _{i=1}^k \frac{t_i}{\|\mathbf{z}_i - \mathbf{u}\|^{2}} \Big). \end{align*} $$
Thus, we continue
 $$ \begin{align*} \Big( \sum _{i=1}^k t_i \frac{\mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^* &= (\mathbf{v} - \mathbf{u})^*\Big( \frac{1}{\|\mathbf{v} - \mathbf{u}\|^{2}} - \sum _{i=1}^k \frac{t_i}{\|\mathbf{z}_i - \mathbf{u}\|^{2}} \Big)^{-1}\\ &= (\mathbf{v} - \mathbf{u})^* \|\mathbf{v} - \mathbf{u}\|^2 \Big( 1 - \sum _{i=1}^k {t_i}\frac{\|\mathbf{v} - \mathbf{u}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}\\ &= (\mathbf{u} - \mathbf{v})\Big( \sum _{i=1}^k t_i \frac{\|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}, \end{align*} $$
$$ \begin{align*} \Big( \sum _{i=1}^k t_i \frac{\mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^* &= (\mathbf{v} - \mathbf{u})^*\Big( \frac{1}{\|\mathbf{v} - \mathbf{u}\|^{2}} - \sum _{i=1}^k \frac{t_i}{\|\mathbf{z}_i - \mathbf{u}\|^{2}} \Big)^{-1}\\ &= (\mathbf{v} - \mathbf{u})^* \|\mathbf{v} - \mathbf{u}\|^2 \Big( 1 - \sum _{i=1}^k {t_i}\frac{\|\mathbf{v} - \mathbf{u}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}\\ &= (\mathbf{u} - \mathbf{v})\Big( \sum _{i=1}^k t_i \frac{\|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}, \end{align*} $$
where in the last equality, we used part (c) of Lemma 4.1. Define
 $$ \begin{align} \mu_i := \frac{ {t_i \|\mathbf{z}_i - \mathbf{v}\|^2}\|\mathbf{z}_i - \mathbf{u} \|^{-2}}{\sum _{j=1}^k {t_j \|\mathbf{z}_j - \mathbf{v} \|^2}\|\mathbf{z}_j - \mathbf{u} \|^{-2}} \ge 0, \end{align} $$
$$ \begin{align} \mu_i := \frac{ {t_i \|\mathbf{z}_i - \mathbf{v}\|^2}\|\mathbf{z}_i - \mathbf{u} \|^{-2}}{\sum _{j=1}^k {t_j \|\mathbf{z}_j - \mathbf{v} \|^2}\|\mathbf{z}_j - \mathbf{u} \|^{-2}} \ge 0, \end{align} $$
and note that
![]() $\sum _{i=1}^k \mu _i =1$
. Using the above calculation in the second equality below, we get
$\sum _{i=1}^k \mu _i =1$
. Using the above calculation in the second equality below, we get
 $$ \begin{align*} \Big( \sum _{i=1}^k \mu_i (\mathbf{z}_i - \mathbf{v})^*\Big)^*&= \Big({\sum _{i=1}^k t_i\frac{ \|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2}} \Big)\Big( \sum _{i=1}^k t_i\frac{ \mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^*\\ &= \Big({\sum _{i=1}^k t_i \frac{ \|\mathbf{z}_i - \mathbf{v} \|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2}} \Big) (\mathbf{u} - \mathbf{v})\Big( \sum _{i=1}^k t_i\frac{\|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}\\ &= \mathbf{u} -\mathbf{v}. \end{align*} $$
$$ \begin{align*} \Big( \sum _{i=1}^k \mu_i (\mathbf{z}_i - \mathbf{v})^*\Big)^*&= \Big({\sum _{i=1}^k t_i\frac{ \|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2}} \Big)\Big( \sum _{i=1}^k t_i\frac{ \mathbf{z}_i - \mathbf{v}}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^*\\ &= \Big({\sum _{i=1}^k t_i \frac{ \|\mathbf{z}_i - \mathbf{v} \|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2}} \Big) (\mathbf{u} - \mathbf{v})\Big( \sum _{i=1}^k t_i\frac{\|\mathbf{z}_i - \mathbf{v}\|^2}{\|\mathbf{z}_i - \mathbf{u}\|^2} \Big)^{-1}\\ &= \mathbf{u} -\mathbf{v}. \end{align*} $$
Adding
![]() $\mathbf {v}$
to the first and last terms of the above equalities, we conclude
$\mathbf {v}$
to the first and last terms of the above equalities, we conclude
 $$ \begin{align*}\mathbf{u} = \mathbf{v} + \Big( \sum _{i=1}^k \mu_i (\mathbf{z}_i - \mathbf{v})^*\Big)^*, \end{align*} $$
$$ \begin{align*}\mathbf{u} = \mathbf{v} + \Big( \sum _{i=1}^k \mu_i (\mathbf{z}_i - \mathbf{v})^*\Big)^*, \end{align*} $$
and hence,
![]() $\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{\mathbf {z}_1, \ldots , \mathbf {z}_k\}$
.
$\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{\mathbf {z}_1, \ldots , \mathbf {z}_k\}$
.
Since a set is unbounded when its closure contains the point
![]() $\infty $
, we get the following corollary.
$\infty $
, we get the following corollary.
Corollary 4.4 Let
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
![]() $\mathbb {R}^n$
. The set
$\mathbb {R}^n$
. The set
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is unbounded if and only if
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is unbounded if and only if
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
.
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
.
Define the relative interior of
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
to be the set
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
to be the set
In other words, this is the preimage under
![]() $T_{\mathbf {u}}$
of the relative interior of the convex set
$T_{\mathbf {u}}$
of the relative interior of the convex set
![]() $T_{\mathbf {u}}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\})$
. Using Theorem 6.9 in [Reference Rockafellar10], it is not difficult to see that
$T_{\mathbf {u}}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\})$
. Using Theorem 6.9 in [Reference Rockafellar10], it is not difficult to see that
 $$ \begin{align*}\mbox{ri } \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots, \mathbf{z}_k\} = \Big\{ \mathbf{u} +\Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* : t_i> 0 \text{ with } \sum _{i=1}^k t_i = 1 \Big\}. \end{align*} $$
$$ \begin{align*}\mbox{ri } \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots, \mathbf{z}_k\} = \Big\{ \mathbf{u} +\Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* : t_i> 0 \text{ with } \sum _{i=1}^k t_i = 1 \Big\}. \end{align*} $$
Then, from formulae (4.1) in the proof of Theorem 4.3, we obtain the next corollary.
Corollary 4.5 Let
![]() $\mathbf {u} ,\mathbf {v} ,\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. Then,
$\mathbf {u} ,\mathbf {v} ,\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. Then,
![]() $\mathbf {v}$
is in the relative interior (resp. boundary) of
$\mathbf {v}$
is in the relative interior (resp. boundary) of
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
if and only if
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
if and only if
![]() $\mathbf {u}$
is in the relative interior (resp. boundary) of
$\mathbf {u}$
is in the relative interior (resp. boundary) of
![]() $\mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots ,\mathbf {z}_k\}$
.
$\mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots ,\mathbf {z}_k\}$
.
Definition 4.1 Let
![]() $\mathbf {u},\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. We say that
$\mathbf {u},\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. We say that
![]() $\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
is a
$\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
is a
![]() $\mathbf {u}$
-extreme point if it cannot be written as a
$\mathbf {u}$
-extreme point if it cannot be written as a
![]() $\mathbf {u}$
-convex combination, with positive coefficients, of any two distinct points in
$\mathbf {u}$
-convex combination, with positive coefficients, of any two distinct points in
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
Equivalently,
![]() $\mathbf {v}$
is
$\mathbf {v}$
is
![]() $\mathbf {u}$
-extreme if
$\mathbf {u}$
-extreme if
![]() $T_{\mathbf {u}} (\mathbf {v})$
is an extreme point of the convex set
$T_{\mathbf {u}} (\mathbf {v})$
is an extreme point of the convex set
![]() $\mathrm {conv}\{ T_{\mathbf {u}} (\mathbf {z}_1 ), \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) \}$
. This shows, using classical convex analysis, that the extreme points of
$\mathrm {conv}\{ T_{\mathbf {u}} (\mathbf {z}_1 ), \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) \}$
. This shows, using classical convex analysis, that the extreme points of
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
are among the points
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
are among the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
. Thus, we have the following corollary.
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
. Thus, we have the following corollary.
Corollary 4.6 Let
![]() $\mathbf {u} ,\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. Then,
$\mathbf {u} ,\mathbf {z}_1 ,\ldots ,\mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct points. Then,
![]() $\mathbf {z}_i$
is a
$\mathbf {z}_i$
is a
![]() $\mathbf {u}$
-extreme point of
$\mathbf {u}$
-extreme point of
![]() $\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
if and only if
$\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
if and only if
![]() $\mathbf {u} \not \in \mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
.
$\mathbf {u} \not \in \mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
.
Proof To see necessity, fix an
![]() $i \in \{ 1 ,\ldots , k \}$
and assume
$i \in \{ 1 ,\ldots , k \}$
and assume
Since
![]() $\mathbf {u} \neq \mathbf {z}_i$
, there are
$\mathbf {u} \neq \mathbf {z}_i$
, there are
![]() $t_j \in [0,1]$
, for
$t_j \in [0,1]$
, for
![]() $j \in \{1 , \ldots , k \} \smallsetminus \{i \}$
, such that
$j \in \{1 , \ldots , k \} \smallsetminus \{i \}$
, such that
Moreover, since
![]() $\mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}\smallsetminus \{\mathbf {z}_i \}$
, none of the
$\mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}\smallsetminus \{\mathbf {z}_i \}$
, none of the
![]() $t_j$
can be
$t_j$
can be
![]() $1$
. So,
$1$
. So,
![]() $\mathbf {u}$
is not a
$\mathbf {u}$
is not a
![]() $\mathbf {z}_i$
-extreme point of
$\mathbf {z}_i$
-extreme point of
![]() $\mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
. Using Theorem 4.3,
$\mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
. Using Theorem 4.3,
![]() $\mathbf {z}_i \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
, and by definition,
$\mathbf {z}_i \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
, and by definition,
![]() $\mathbf {z}_i$
is not a
$\mathbf {z}_i$
is not a
![]() $\mathbf {u}$
-extreme point. The argument for the sufficiency is similar.
$\mathbf {u}$
-extreme point. The argument for the sufficiency is similar.
Remark 4.7. If one takes
![]() $\mathbf {u} = \infty $
in Corollary 4.6, we get that
$\mathbf {u} = \infty $
in Corollary 4.6, we get that
![]() $\mathbf {z}_i$
is a
$\mathbf {z}_i$
is a
![]() $\mathbf {u}$
-extreme point of
$\mathbf {u}$
-extreme point of
![]() $\mathrm {conv} \{\mathbf {z}_1, \ldots , \mathbf {z}_k\}$
if and only if
$\mathrm {conv} \{\mathbf {z}_1, \ldots , \mathbf {z}_k\}$
if and only if
![]() $\infty \not \in \mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
. Using Theorem 4.3, the latter condition is equivalent to
$\infty \not \in \mathrm {conv}_{\mathbf {z}_i} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
. Using Theorem 4.3, the latter condition is equivalent to
![]() $\mathbf {z}_i \not \in \mathrm {conv}\{\mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
, which is equivalent to the definition of an extreme point in classical convex analysis.
$\mathbf {z}_i \not \in \mathrm {conv}\{\mathbf {z}_1 , \ldots , \mathbf {z}_{i-1} , \mathbf {z}_{i+1}, \ldots , \mathbf {z}_k \}$
, which is equivalent to the definition of an extreme point in classical convex analysis.
Corollary 4.8 Let
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
and
$\mathbf {u} \in \hat {\mathbb {R}}^n$
and
![]() $Z\subset \hat {\mathbb {R}}^n$
be a
$Z\subset \hat {\mathbb {R}}^n$
be a
![]() $\mathbf {u}$
-convex set, not containing
$\mathbf {u}$
-convex set, not containing
![]() $\mathbf {u}$
. Then,
$\mathbf {u}$
. Then,
![]() $\mathbf {v} \in Z$
is a
$\mathbf {v} \in Z$
is a
![]() $\mathbf {u}$
-extreme point if and only if
$\mathbf {u}$
-extreme point if and only if
![]() $\mathbf {u} \not \in \mathrm {conv}_{\mathbf {v}} (Z)$
.
$\mathbf {u} \not \in \mathrm {conv}_{\mathbf {v}} (Z)$
.
Proof If
![]() $\mathbf {v}$
is not a
$\mathbf {v}$
is not a
![]() $\mathbf {u}$
-extreme point, then there are points
$\mathbf {u}$
-extreme point, then there are points
![]() $\mathbf {z}_1, \mathbf {z}_2 \in Z$
distinct from
$\mathbf {z}_1, \mathbf {z}_2 \in Z$
distinct from
![]() $\mathbf {v}$
such that
$\mathbf {v}$
such that
![]() $\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1, \mathbf {z}_2 \}$
. Therefore,
$\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1, \mathbf {z}_2 \}$
. Therefore,
![]() $\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \mathbf {z}_2 \} \subseteq \mathrm {conv}_{\mathbf {v}} (Z)$
. Conversely, if
$\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \mathbf {z}_2 \} \subseteq \mathrm {conv}_{\mathbf {v}} (Z)$
. Conversely, if
![]() $\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} (Z)$
, then by Carathéodory’s theorem, there are points
$\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} (Z)$
, then by Carathéodory’s theorem, there are points
![]() $ \mathbf {z}_1, \ldots , \mathbf {z}_k \in Z$
, for some
$ \mathbf {z}_1, \ldots , \mathbf {z}_k \in Z$
, for some
![]() $k \le n+1$
, distinct from
$k \le n+1$
, distinct from
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\mathbf {v}$
, such that
$\mathbf {v}$
, such that
![]() $\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_{k} \}$
. This implies that
$\mathbf {u} \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_{k} \}$
. This implies that
![]() $\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_{k} \}$
. Therefore,
$\mathbf {v} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_{k} \}$
. Therefore,
![]() $\mathbf {v}$
cannot be
$\mathbf {v}$
cannot be
![]() $\mathbf {u}$
-extreme.
$\mathbf {u}$
-extreme.
With the notation from the last corollary, note that if
![]() $\mathbf {v} \in \mathrm {int}(Z)$
, then
$\mathbf {v} \in \mathrm {int}(Z)$
, then
![]() $\mathrm {conv}_{\mathbf {v}} (Z) = \hat {\mathbb {R}}^n$
; therefore, no point in the interior of Z can be a
$\mathrm {conv}_{\mathbf {v}} (Z) = \hat {\mathbb {R}}^n$
; therefore, no point in the interior of Z can be a
![]() $\mathbf {u}$
-extreme point.
$\mathbf {u}$
-extreme point.
Proposition 4.9 Let
![]() $\mathbf {u} ,\mathbf {v} , \mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
$\mathbf {u} ,\mathbf {v} , \mathbf {z}_1, \ldots , \mathbf {z}_k$
be distinct points in
![]() $\hat {\mathbb {R}}^n$
, not all on a circle. Then, neither of the sets
$\hat {\mathbb {R}}^n$
, not all on a circle. Then, neither of the sets
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and
![]() $\mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is contained in the other.
$\mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is contained in the other.
Proof Without loss of generality, we may assume
![]() $\mathbf {u} = \infty $
, so
$\mathbf {u} = \infty $
, so
![]() $\mathbf {v} , \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \mathbb {R}^n$
. The assumption that the points are not on a circle now becomes that they are not on a line. We show that
$\mathbf {v} , \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \mathbb {R}^n$
. The assumption that the points are not on a circle now becomes that they are not on a line. We show that
with the opposite non-inclusion being analogous. Since the points are not all on a circle, there are at least two distinct points in
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k$
(i.e.,
$\mathbf {z}_1 , \ldots , \mathbf {z}_k$
(i.e.,
![]() $k \geq 2$
). Since
$k \geq 2$
). Since
![]() $\mathbf {v} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, we have that
$\mathbf {v} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, we have that
![]() $\mathbf {v} \not \in \mathrm {conv}_{\mathbf {v}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. If
$\mathbf {v} \not \in \mathrm {conv}_{\mathbf {v}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. If
![]() $\mathbf {v} \in \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, then we are done. Assume this is not the case. Then, there is a closed half-space H containing
$\mathbf {v} \in \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, then we are done. Assume this is not the case. Then, there is a closed half-space H containing
![]() $\mathrm {conv}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
having at least two points
$\mathrm {conv}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
having at least two points
![]() $\mathbf {z}_i , \mathbf {z}_j$
on the boundary and not containing
$\mathbf {z}_i , \mathbf {z}_j$
on the boundary and not containing
![]() $\mathbf {v}$
. (Note that if the points
$\mathbf {v}$
. (Note that if the points
![]() $\mathbf {v}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
are on a line, such a half-space does not exist.) Let
$\mathbf {v}, \mathbf {z}_1, \ldots , \mathbf {z}_k$
are on a line, such a half-space does not exist.) Let
![]() $\mathbf {z} \in \mathrm {conv}\{ \mathbf {z}_i , \mathbf {z}_j\} \smallsetminus \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
; that is,
$\mathbf {z} \in \mathrm {conv}\{ \mathbf {z}_i , \mathbf {z}_j\} \smallsetminus \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
; that is,
![]() $\mathbf {z} \in \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. Since H is also
$\mathbf {z} \in \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. Since H is also
![]() $\mathbf {z}$
-convex, we get that
$\mathbf {z}$
-convex, we get that
![]() $\mathbf {v} \not \in \mathrm {conv}_{\mathbf {z}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \subseteq H$
. By Theorem 4.3, we obtain that
$\mathbf {v} \not \in \mathrm {conv}_{\mathbf {z}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \subseteq H$
. By Theorem 4.3, we obtain that
![]() ${\mathbf {z} \not \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}}$
, concluding the argument.
${\mathbf {z} \not \in \mathrm {conv}_{\mathbf {v}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}}$
, concluding the argument.
Note that the proposition fails if the points are on a circle. For example, take
![]() $\mathbf {z}_1$
,
$\mathbf {z}_1$
,
![]() $\mathbf {z}_2$
,
$\mathbf {z}_2$
,
![]() $\mathbf {u}$
, and
$\mathbf {u}$
, and
![]() $\mathbf {v}$
in this order, clockwise on a circle. Then, according to Proposition 3.3, we have
$\mathbf {v}$
in this order, clockwise on a circle. Then, according to Proposition 3.3, we have
5 Theorems of the alternatives
Analogous to classical convexity, we prove a separation theorem involving polar convex sets. This naturally leads into theorems of alternatives. However, where theorems of alternatives usually imply the existence of
![]() $1$
-forms or solutions to linear systems in the classical setting, theorems of alternatives in the polar setting imply existence of
$1$
-forms or solutions to linear systems in the classical setting, theorems of alternatives in the polar setting imply existence of
![]() $2$
-forms. We start by noting a few simple facts. We refer the reader to [Reference Rockafellar10, Section 11] to recall the various versions of the hyperplane separation theorem.
$2$
-forms. We start by noting a few simple facts. We refer the reader to [Reference Rockafellar10, Section 11] to recall the various versions of the hyperplane separation theorem.
Definition 5.1 A spherical domain
![]() $S \subseteq \hat {\mathbb {R}}^n$
is said to separate two sets
$S \subseteq \hat {\mathbb {R}}^n$
is said to separate two sets
![]() $A , B \subseteq \hat {\mathbb {R}}^n$
if either
$A , B \subseteq \hat {\mathbb {R}}^n$
if either
![]() $A \subseteq S$
and
$A \subseteq S$
and
![]() $B \subseteq \mathrm {cl}(S^c)$
or
$B \subseteq \mathrm {cl}(S^c)$
or
![]() $B \subseteq S$
and
$B \subseteq S$
and
![]() $A \subseteq \mathrm {cl}(S^c)$
. Such a spherical domain (or the boundary of the spherical domain) is called a separating spherical domain (or separating sphere) for the pair
$A \subseteq \mathrm {cl}(S^c)$
. Such a spherical domain (or the boundary of the spherical domain) is called a separating spherical domain (or separating sphere) for the pair
![]() $A, B$
. We say that S strongly separates A and B if it separates these sets and
$A, B$
. We say that S strongly separates A and B if it separates these sets and
![]() $A \cap \partial S = \emptyset = B \cap \partial S$
.
$A \cap \partial S = \emptyset = B \cap \partial S$
.
Lemma 5.1 (Spherical separation)
If
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
and A, B are nonintersecting
$\mathbf {u} \in \hat {\mathbb {R}}^n$
and A, B are nonintersecting
![]() $\mathbf {u}$
-convex sets in
$\mathbf {u}$
-convex sets in
![]() $\hat {\mathbb {R}}^n$
, then there exists a
$\hat {\mathbb {R}}^n$
, then there exists a
![]() $(n-1)$
-spherical domain S, having
$(n-1)$
-spherical domain S, having
![]() $\mathbf {u}$
on its boundary, which separates A and B. Moreover, if
$\mathbf {u}$
on its boundary, which separates A and B. Moreover, if
![]() $\mathbf {u} \not \in A \cup B$
and one of the following holds,
$\mathbf {u} \not \in A \cup B$
and one of the following holds,
-
(1) A is closed in
 $\hat {\mathbb {R}}^n$
and B is closed in
$\hat {\mathbb {R}}^n$
and B is closed in
 $\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
, or
$\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
, or -
(2) A and B are both open,
then S can be chosen to strongly separate A and B, still having
![]() $\mathbf {u}$
on its boundary.
$\mathbf {u}$
on its boundary.
Proof Note that
![]() $T_{\mathbf {u}}(A)$
and
$T_{\mathbf {u}}(A)$
and
![]() $T_{\mathbf {u}}(B)$
are nonintersecting convex sets. The classical hyperplane separation theorem implies that there is a hyperplane H that separates
$T_{\mathbf {u}}(B)$
are nonintersecting convex sets. The classical hyperplane separation theorem implies that there is a hyperplane H that separates
![]() $T_{\mathbf {u}}(A)$
and
$T_{\mathbf {u}}(A)$
and
![]() $T_{\mathbf {u}}(B)$
. Then,
$T_{\mathbf {u}}(B)$
. Then,
![]() $T_{\mathbf {u}}(H)$
is an
$T_{\mathbf {u}}(H)$
is an
![]() $(n-1)$
-sphere, having
$(n-1)$
-sphere, having
![]() $\mathbf {u}$
on its boundary, separating A and B. Next, note that if
$\mathbf {u}$
on its boundary, separating A and B. Next, note that if
![]() $\mathbf {u} \not \in A \cup B$
, then
$\mathbf {u} \not \in A \cup B$
, then
![]() $T_{\mathbf {u}} (A) , T_{\mathbf {u}} (B) \subseteq \mathbb {R}^n$
.
$T_{\mathbf {u}} (A) , T_{\mathbf {u}} (B) \subseteq \mathbb {R}^n$
.
(1) If A is closed as a subset of
![]() $\hat {\mathbb {R}}^n$
, then it is compact. Since
$\hat {\mathbb {R}}^n$
, then it is compact. Since
![]() $\mathbf {u} \not \in A$
,
$\mathbf {u} \not \in A$
,
![]() $T_{\mathbf {u}} (A)$
is compact in
$T_{\mathbf {u}} (A)$
is compact in
![]() $\mathbb {R}^n$
. Similarly, if B is closed in
$\mathbb {R}^n$
. Similarly, if B is closed in
![]() $\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
, then
$\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
, then
![]() $T_{\mathbf {u}} (B)$
is closed in
$T_{\mathbf {u}} (B)$
is closed in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
(2) If A and B are both open, then so are the convex sets
![]() $T_{\mathbf {u}} (A)$
and
$T_{\mathbf {u}} (A)$
and
![]() $T_{\mathbf {u}} (B)$
.
$T_{\mathbf {u}} (B)$
.
In both cases, from ordinary convexity, we can find a separating hyperplane H such that
![]() $T_{\mathbf {u}}(A) \cap \partial H = \emptyset = T_{\mathbf {u}}(B) \cap \partial H$
. We conclude by setting
$T_{\mathbf {u}}(A) \cap \partial H = \emptyset = T_{\mathbf {u}}(B) \cap \partial H$
. We conclude by setting
![]() $S:=T_{\mathbf {u}}(H)$
.
$S:=T_{\mathbf {u}}(H)$
.
Lemma 5.2 Let
![]() $Z \subseteq \hat {\mathbb {R}}^n$
be closed and let
$Z \subseteq \hat {\mathbb {R}}^n$
be closed and let
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
be such that
$\mathbf {u} \in \hat {\mathbb {R}}^n$
be such that
![]() $\mathbf {u}\not \in \partial Z$
. Then,
$\mathbf {u}\not \in \partial Z$
. Then,
![]() $\mathrm {conv}_{\mathbf {u}} (Z)$
is closed in
$\mathrm {conv}_{\mathbf {u}} (Z)$
is closed in
![]() $\hat {\mathbb {R}}^n$
.
$\hat {\mathbb {R}}^n$
.
Proof Without loss of generality, we may assume
![]() $\mathbf {u} = \infty $
. If
$\mathbf {u} = \infty $
. If
![]() $\infty \not \in Z$
, then Z is a bounded closed set. So we can conclude that
$\infty \not \in Z$
, then Z is a bounded closed set. So we can conclude that
![]() $\mathrm {conv}(Z)$
is closed. Otherwise,
$\mathrm {conv}(Z)$
is closed. Otherwise,
![]() $\infty \in \mathrm {int}(Z)$
. Then,
$\infty \in \mathrm {int}(Z)$
. Then,
![]() $\mathrm {conv}(Z) = \hat {\mathbb {R}}^n$
, so we are done.
$\mathrm {conv}(Z) = \hat {\mathbb {R}}^n$
, so we are done.
Example 5.3. Note that the assumption
![]() $\mathbf {u}\not \in \partial Z$
in Lemma 5.2 is necessary. Indeed, take the set
$\mathbf {u}\not \in \partial Z$
in Lemma 5.2 is necessary. Indeed, take the set
and take the pole
![]() $u = 1$
. Notice that both
$u = 1$
. Notice that both
![]() $0$
and
$0$
and
![]() $(1 + i)/2$
lie on the circle
$(1 + i)/2$
lie on the circle
![]() $|z-1/2| = 1/2$
, which also passes through u. Then, it can be shown that
$|z-1/2| = 1/2$
, which also passes through u. Then, it can be shown that
which is not closed. The situation is illustrated in Figure 1.
Lemma 5.4 (Gordan’s lemma)
Let
![]() $\mathbf {u}, \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, such that
$\mathbf {u}, \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, such that
![]() $\mathbf {u} \neq \mathbf {0}, \infty $
. Then either there are numbers
$\mathbf {u} \neq \mathbf {0}, \infty $
. Then either there are numbers
![]() $t_1 , \ldots , t_k \in [0,1]$
with
$t_1 , \ldots , t_k \in [0,1]$
with
![]() $\sum _{i=1}^k t_i = 1$
such that
$\sum _{i=1}^k t_i = 1$
such that
 $$ \begin{align} (\mathbf{0}-\mathbf{u})^* = \sum _{i=1}^k t_i(\mathbf{z}_i - \mathbf{u})^*, \end{align} $$
$$ \begin{align} (\mathbf{0}-\mathbf{u})^* = \sum _{i=1}^k t_i(\mathbf{z}_i - \mathbf{u})^*, \end{align} $$
or there exist some
![]() $\mathbf {a} \in \mathbb {R}^n$
,
$\mathbf {a} \in \mathbb {R}^n$
,
![]() $\alpha , \beta \in \mathbb {R}$
, with
$\alpha , \beta \in \mathbb {R}$
, with
![]() $\beta>0$
such that
$\beta>0$
such that

Figure 1: The set Z (in black) and its u-convex hull (in orange).
Proof Note that Equation (5.1) is the same as saying that
![]() $\mathbf {0} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Assume that this is not the case. Since
$\mathbf {0} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Assume that this is not the case. Since
![]() $ \mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, the set
$ \mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, the set
![]() $\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is closed. So, by Lemma 5.1, there is a spherical domain S, having
$\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is closed. So, by Lemma 5.1, there is a spherical domain S, having
![]() $\mathbf {u}$
on its boundary, that strongly separates
$\mathbf {u}$
on its boundary, that strongly separates
![]() $\{ \mathbf {0} \}$
and
$\{ \mathbf {0} \}$
and
![]() $\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
; that is,
$\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
; that is,
Let
![]() $\alpha \langle \mathbf {x} , \mathbf {x} \rangle + \langle \mathbf {x} , \mathbf {v} \rangle + \beta = 0$
be the equation of the boundary of the spherical domain S. Since it separates
$\alpha \langle \mathbf {x} , \mathbf {x} \rangle + \langle \mathbf {x} , \mathbf {v} \rangle + \beta = 0$
be the equation of the boundary of the spherical domain S. Since it separates
![]() $\{ \mathbf {0} \}$
and
$\{ \mathbf {0} \}$
and
![]() $\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, both of them evaluate to different signs and neither of them are zero. In particular, since
$\mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, both of them evaluate to different signs and neither of them are zero. In particular, since
![]() $\mathbf {0} \not \in \partial S$
, we have
$\mathbf {0} \not \in \partial S$
, we have
If
![]() $\beta> 0$
, we are done; otherwise, take
$\beta> 0$
, we are done; otherwise, take
![]() $-\mathbf {a}$
,
$-\mathbf {a}$
,
![]() $-\alpha $
, and
$-\alpha $
, and
![]() $-\beta $
to get the inequalities in (5.2). Since
$-\beta $
to get the inequalities in (5.2). Since
![]() $\mathbf {u} \in \partial S$
, we get the equality in (5.2).
$\mathbf {u} \in \partial S$
, we get the equality in (5.2).
Remark 5.5. Lemma 5.4 implies the classical Gordan’s lemma. Indeed, applying
![]() $*$
and adding
$*$
and adding
![]() $\mathbf {u}$
to both sides of (5.1) give
$\mathbf {u}$
to both sides of (5.1) give
 $$ \begin{align*} \mathbf{0} = \mathbf{u} + \Big( \sum_{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big)^*. \end{align*} $$
$$ \begin{align*} \mathbf{0} = \mathbf{u} + \Big( \sum_{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^*\Big)^*. \end{align*} $$
Taking limits as
![]() $\mathbf {u} \to \infty $
and using Lemma 2.1, we see that (5.1) converges to
$\mathbf {u} \to \infty $
and using Lemma 2.1, we see that (5.1) converges to
 $$ \begin{align*} \mathbf{0} = \sum_{i=1}^k t_i \mathbf{z}_i. \end{align*} $$
$$ \begin{align*} \mathbf{0} = \sum_{i=1}^k t_i \mathbf{z}_i. \end{align*} $$
This is equivalent to saying that
![]() $\mathbf {0} \in \mathrm {conv}\{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
$\mathbf {0} \in \mathrm {conv}\{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
However, if
![]() $\mathbf {0} \not \in \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and letting
$\mathbf {0} \not \in \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and letting
![]() $\mathbf {u}$
converge to
$\mathbf {u}$
converge to
![]() $\infty $
, the strongly separating sphere in the proof of Lemma 5.4 becomes a hyperplane since it is chosen to pass through the pole
$\infty $
, the strongly separating sphere in the proof of Lemma 5.4 becomes a hyperplane since it is chosen to pass through the pole
![]() $\mathbf {u}$
. By case (1) of Lemma 5.1, it can be chosen to be strongly separating. Let its equation be
$\mathbf {u}$
. By case (1) of Lemma 5.1, it can be chosen to be strongly separating. Let its equation be
![]() $\langle \mathbf {z} , \mathbf {a} \rangle + \beta = 0$
. We may choose the sign of
$\langle \mathbf {z} , \mathbf {a} \rangle + \beta = 0$
. We may choose the sign of
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\beta $
so that
$\beta $
so that
Since the hyperplane is strongly separating the sets
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
![]() $\{ \mathbf {0} \}$
, we must have
$\{ \mathbf {0} \}$
, we must have
![]() $\langle \mathbf {0}, \mathbf {a} \rangle + \beta>0$
; that is,
$\langle \mathbf {0}, \mathbf {a} \rangle + \beta>0$
; that is,
![]() $\beta> 0$
. Combining with the previous equation, we get
$\beta> 0$
. Combining with the previous equation, we get
thus recovering the equations of the alternative in the classical Gordan’s lemma; see [Reference Borwein and Lewis2, Theorem 2.2.1].
Lemma 5.6 Let
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and not all
$\mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and not all
![]() $\mathbf {0}$
and let
$\mathbf {0}$
and let
 $$ \begin{align*}\mathbf{u} := - \sum _{i=1}^k t_i \mathbf{z}_i \mbox{ for some } t_1, \ldots , t_k \in [0 , \infty ). \end{align*} $$
$$ \begin{align*}\mathbf{u} := - \sum _{i=1}^k t_i \mathbf{z}_i \mbox{ for some } t_1, \ldots , t_k \in [0 , \infty ). \end{align*} $$
Suppose
![]() $\mathbf {u}$
is distinct from
$\mathbf {u}$
is distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
and let
![]() $\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \infty , \mathbf {u} \}$
. Then, either there are numbers
$\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \infty , \mathbf {u} \}$
. Then, either there are numbers
![]() $\alpha _1 , \ldots , \alpha _k \in [0 , \infty )$
, such that
$\alpha _1 , \ldots , \alpha _k \in [0 , \infty )$
, such that
 $$ \begin{align} \mathbf{v} = \sum _{i=1}^k \alpha_i \mathbf{z}_i \end{align} $$
$$ \begin{align} \mathbf{v} = \sum _{i=1}^k \alpha_i \mathbf{z}_i \end{align} $$
or there exist
![]() $\mathbf {a} \in \mathbb {R}^n$
and
$\mathbf {a} \in \mathbb {R}^n$
and
![]() $\alpha , \beta \in \mathbb {R}$
, with
$\alpha , \beta \in \mathbb {R}$
, with
![]() $\alpha \geq 0$
, such that
$\alpha \geq 0$
, such that
 $$ \begin{align} \alpha \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i , \mathbf{a} \rangle + \beta &> 0, \mbox{ for all } i=1,\ldots, k, \nonumber \\ \alpha \langle \mathbf{v} , \mathbf{v} \rangle + \langle \mathbf{v} , \mathbf{a} \rangle + \beta &< 0, \mbox{ and } \\ \alpha \langle \mathbf{u} , \mathbf{u} \rangle + \langle \mathbf{u} , \mathbf{a} \rangle + \beta &= 0. \nonumber \end{align} $$
$$ \begin{align} \alpha \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i , \mathbf{a} \rangle + \beta &> 0, \mbox{ for all } i=1,\ldots, k, \nonumber \\ \alpha \langle \mathbf{v} , \mathbf{v} \rangle + \langle \mathbf{v} , \mathbf{a} \rangle + \beta &< 0, \mbox{ and } \\ \alpha \langle \mathbf{u} , \mathbf{u} \rangle + \langle \mathbf{u} , \mathbf{a} \rangle + \beta &= 0. \nonumber \end{align} $$
Proof If
![]() $\mathbf {u} = - \sum _{i=1}^k t_i \mathbf {z}_i$
for
$\mathbf {u} = - \sum _{i=1}^k t_i \mathbf {z}_i$
for
![]() $t_i \in [0, \infty )$
, then
$t_i \in [0, \infty )$
, then
![]() $\mathbf {u} \in -\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, and so
$\mathbf {u} \in -\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, and so
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is
![]() $\mathbf {u}$
-convex. (The argument for the latter is analogous to the one in Example 2.6.) Consequently,
$\mathbf {u}$
-convex. (The argument for the latter is analogous to the one in Example 2.6.) Consequently,
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\} \cup \{ \infty \}$
is also
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\} \cup \{ \infty \}$
is also
![]() $\mathbf {u}$
-convex. Thus, for any
$\mathbf {u}$
-convex. Thus, for any
![]() $\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \infty , \mathbf {u} \}$
, either
$\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \infty , \mathbf {u} \}$
, either
![]() $\mathbf {v} \in \mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
or there exists a spherical domain S, having
$\mathbf {v} \in \mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
or there exists a spherical domain S, having
![]() $\mathbf {u}$
on its boundary, separating
$\mathbf {u}$
on its boundary, separating
![]() $\mathbf {v}$
and
$\mathbf {v}$
and
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}\cup \{ \infty \}$
. Again, since
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}\cup \{ \infty \}$
. Again, since
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}\cup \{ \infty \}$
is closed, this domain can be chosen so that
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}\cup \{ \infty \}$
is closed, this domain can be chosen so that
Let
![]() $\alpha \langle \mathbf {x} , \mathbf {x} \rangle + \langle \mathbf {x} , \mathbf {a} \rangle + \beta = 0$
be the equation of the boundary of the spherical domain S. Since
$\alpha \langle \mathbf {x} , \mathbf {x} \rangle + \langle \mathbf {x} , \mathbf {a} \rangle + \beta = 0$
be the equation of the boundary of the spherical domain S. Since
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is an unbounded set, it must lie in an unbounded component of
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is an unbounded set, it must lie in an unbounded component of
![]() $\mathbb {R}^n \smallsetminus \partial S$
. If
$\mathbb {R}^n \smallsetminus \partial S$
. If
![]() $\partial S$
happens to be a hyperplane, then
$\partial S$
happens to be a hyperplane, then
![]() $\alpha =0$
, and we can choose the signs of
$\alpha =0$
, and we can choose the signs of
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\beta $
to satisfy (5.4). Otherwise,
$\beta $
to satisfy (5.4). Otherwise,
![]() $\mathbb {R}^n \smallsetminus \partial S$
has only one unbounded component, and we can choose the coefficient
$\mathbb {R}^n \smallsetminus \partial S$
has only one unbounded component, and we can choose the coefficient
![]() $\alpha $
to be positive. Then, since
$\alpha $
to be positive. Then, since
![]() $\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is an unbounded set, the quadratic term in
$\mathrm {cone}\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
is an unbounded set, the quadratic term in
![]() $\alpha \langle \mathbf {z}_i , \mathbf {z}_i \rangle + \langle \mathbf {z}_i , \mathbf {a} \rangle + \beta $
determines the sign of the whole expression. The inequalities in (5.4) follow. Since
$\alpha \langle \mathbf {z}_i , \mathbf {z}_i \rangle + \langle \mathbf {z}_i , \mathbf {a} \rangle + \beta $
determines the sign of the whole expression. The inequalities in (5.4) follow. Since
![]() $\mathbf {v}$
lies in the bounded component, we have
$\mathbf {v}$
lies in the bounded component, we have
![]() $\alpha \langle \mathbf {v} , \mathbf {v} \rangle + \langle \mathbf {v} , \mathbf {a} \rangle + \beta < 0$
. Finally, the boundary of the spherical domain passes through
$\alpha \langle \mathbf {v} , \mathbf {v} \rangle + \langle \mathbf {v} , \mathbf {a} \rangle + \beta < 0$
. Finally, the boundary of the spherical domain passes through
![]() $\mathbf {u}$
, giving the third statement in (5.4).
$\mathbf {u}$
, giving the third statement in (5.4).
The proof of Lemma 5.6 shows that it is convenient to redefine the cone of
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {R}^n$
from classical convex analysis to include the point at
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {R}^n$
from classical convex analysis to include the point at
![]() $\infty $
as follows:
$\infty $
as follows:
 $$ \begin{align*}\mathrm{cone} \{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} := \Big\{ \sum _{i=1}^k t_i\mathbf{z}_i : t_1 , \ldots , t_k \in [0 , \infty ) \Big\} \cup \{\infty\}. \end{align*} $$
$$ \begin{align*}\mathrm{cone} \{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} := \Big\{ \sum _{i=1}^k t_i\mathbf{z}_i : t_1 , \ldots , t_k \in [0 , \infty ) \Big\} \cup \{\infty\}. \end{align*} $$
This is the union of all rays that pass through
![]() $\mathbf {0}$
,
$\mathbf {0}$
,
![]() $\mathbf {z}$
,
$\mathbf {z}$
,
![]() $\infty $
, for some
$\infty $
, for some
![]() $\mathbf {z} \in \mathrm {conv} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Extend this definition to
$\mathbf {z} \in \mathrm {conv} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Extend this definition to
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
by
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
by
Definition 5.2 Given
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the cone of
$\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the cone of
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k$
with respect to
$\mathbf {z}_1 , \ldots , \mathbf {z}_k$
with respect to
![]() $\mathbf {u}$
by
$\mathbf {u}$
by
 $$ \begin{align*}\mathrm{cone}_{\mathbf{u}} \{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} := \Big\{ \mathbf{u} + \Big( \sum _{i=1}^k t_i(\mathbf{u} + (\mathbf{z}_i - \mathbf{u})^*) - \mathbf{u} \Big)^* : t_1 , \ldots , t_k \in [0 , \infty ) \Big\} \cup \{\mathbf{u}\}. \end{align*} $$
$$ \begin{align*}\mathrm{cone}_{\mathbf{u}} \{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} := \Big\{ \mathbf{u} + \Big( \sum _{i=1}^k t_i(\mathbf{u} + (\mathbf{z}_i - \mathbf{u})^*) - \mathbf{u} \Big)^* : t_1 , \ldots , t_k \in [0 , \infty ) \Big\} \cup \{\mathbf{u}\}. \end{align*} $$
This is the image under
![]() $T_{\mathbf {u}}$
of
$T_{\mathbf {u}}$
of
![]() $\mathrm {cone}\{T_{\mathbf {u}} (\mathbf {z}_1) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k)\} \cup \{\infty \}$
, and so it is
$\mathrm {cone}\{T_{\mathbf {u}} (\mathbf {z}_1) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k)\} \cup \{\infty \}$
, and so it is
![]() $\mathbf {u}$
-convex. Note that
$\mathbf {u}$
-convex. Note that
![]() $T_{\mathbf {u}}(\mathbf {0}) = \mathbf {u}-\mathbf {u}^*$
. Geometrically,
$T_{\mathbf {u}}(\mathbf {0}) = \mathbf {u}-\mathbf {u}^*$
. Geometrically,
![]() $ \mathrm {cone}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is the union of all circular arcs that pass through
$ \mathrm {cone}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is the union of all circular arcs that pass through
![]() $\mathbf {u}-\mathbf {u}^*$
,
$\mathbf {u}-\mathbf {u}^*$
,
![]() $\mathbf {z}$
,
$\mathbf {z}$
,
![]() $\mathbf {u}$
, for some
$\mathbf {u}$
, for some
![]() $\mathbf {z} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Finally, for any
$\mathbf {z} \in \mathrm {conv}_{\mathbf {u}} \{\mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Finally, for any
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
, define
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
, define
Figure 2 shows a
![]() $\mathbf {u}$
-cone in
$\mathbf {u}$
-cone in
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.

Figure 2: The cone in
![]() $\mathbb {R}^2$
, with respect to u, determined by the points
$\mathbb {R}^2$
, with respect to u, determined by the points
![]() $z_1$
,
$z_1$
,
![]() $z_2$
, and
$z_2$
, and
![]() $z_3$
(in orange) and the boundary of their u-convex hull (in black).
$z_3$
(in orange) and the boundary of their u-convex hull (in black).
Lemma 5.7 (Farkas’ lemma)
Let
![]() $\mathbf {u} , \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct such that
$\mathbf {u} , \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct such that
![]() $\mathbf {u} \neq \infty $
and let
$\mathbf {u} \neq \infty $
and let
![]() $\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
. Then, either there are numbers
$\mathbf {v} \in \hat {\mathbb {R}}^n \smallsetminus \{ \mathbf {u} \}$
. Then, either there are numbers
![]() $t_1 , \ldots , t_k \in [0 , \infty )$
such that
$t_1 , \ldots , t_k \in [0 , \infty )$
such that
 $$ \begin{align*}\mathbf{u} + (\mathbf{v}-\mathbf{u})^*= \sum _{i=1}^k t_i(\mathbf{u} + (\mathbf{z}_i - \mathbf{u})^*) \end{align*} $$
$$ \begin{align*}\mathbf{u} + (\mathbf{v}-\mathbf{u})^*= \sum _{i=1}^k t_i(\mathbf{u} + (\mathbf{z}_i - \mathbf{u})^*) \end{align*} $$
or there exist an
![]() $\mathbf {a} \in \mathbb {R}^n$
and
$\mathbf {a} \in \mathbb {R}^n$
and
![]() $\alpha , \beta \in \mathbb {R}$
such that
$\alpha , \beta \in \mathbb {R}$
such that
 $$ \begin{align} \alpha \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i , \mathbf{a} \rangle + \beta &\leq 0, \mbox{ for all } i=1,\ldots, k, \nonumber \\ \alpha \langle \mathbf{v} , \mathbf{v} \rangle+ \langle \mathbf{v} , \mathbf{a} \rangle + \beta &> 0, \\ \alpha \langle \mathbf{u} , \mathbf{u} \rangle + \langle \mathbf{u} , \mathbf{a} \rangle + \beta &= 0, \mbox{ and } \nonumber \\ \alpha \langle \mathbf{u}, \mathbf{u} \rangle - \alpha - \beta &= 0. \nonumber \end{align} $$
$$ \begin{align} \alpha \langle \mathbf{z}_i , \mathbf{z}_i \rangle + \langle \mathbf{z}_i , \mathbf{a} \rangle + \beta &\leq 0, \mbox{ for all } i=1,\ldots, k, \nonumber \\ \alpha \langle \mathbf{v} , \mathbf{v} \rangle+ \langle \mathbf{v} , \mathbf{a} \rangle + \beta &> 0, \\ \alpha \langle \mathbf{u} , \mathbf{u} \rangle + \langle \mathbf{u} , \mathbf{a} \rangle + \beta &= 0, \mbox{ and } \nonumber \\ \alpha \langle \mathbf{u}, \mathbf{u} \rangle - \alpha - \beta &= 0. \nonumber \end{align} $$
Proof The first condition is equivalent to
![]() $\mathbf {v} \in \mathrm {cone}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Applying the transform
$\mathbf {v} \in \mathrm {cone}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Applying the transform
![]() $T_{\mathbf {u}}$
to this inclusion, it is equivalent to
$T_{\mathbf {u}}$
to this inclusion, it is equivalent to
![]() $T_{\mathbf {u}}(\mathbf {v}) \in \mathrm {cone} \{ T_{\mathbf {u}} (\mathbf {z}_1), \ldots , T_{\mathbf {u}}(\mathbf {z}_k ) \}$
. Assume this is not the case. Using the classical Farkas’ lemma, we get that there is a closed half-space H supporting
$T_{\mathbf {u}}(\mathbf {v}) \in \mathrm {cone} \{ T_{\mathbf {u}} (\mathbf {z}_1), \ldots , T_{\mathbf {u}}(\mathbf {z}_k ) \}$
. Assume this is not the case. Using the classical Farkas’ lemma, we get that there is a closed half-space H supporting
![]() $\mathrm {cone} \{ T_{\mathbf {u}} (\mathbf {z}_1), \ldots , T_{\mathbf {u}}(\mathbf {z}_k ) \}$
at
$\mathrm {cone} \{ T_{\mathbf {u}} (\mathbf {z}_1), \ldots , T_{\mathbf {u}}(\mathbf {z}_k ) \}$
at
![]() $\mathbf {0}$
and separating it from
$\mathbf {0}$
and separating it from
![]() $\{T_{\mathbf {u}}(\mathbf {v}) \}$
. Moreover, H is such that
$\{T_{\mathbf {u}}(\mathbf {v}) \}$
. Moreover, H is such that
![]() $T_{\mathbf {u}}(\mathbf {v})$
lies in the open complement of H. Apply
$T_{\mathbf {u}}(\mathbf {v})$
lies in the open complement of H. Apply
![]() $T_{\mathbf {u}}$
to the boundary hyperplane
$T_{\mathbf {u}}$
to the boundary hyperplane
![]() $\partial H$
, which contains
$\partial H$
, which contains
![]() $\infty $
by convention; see Example 3.6. We get that
$\infty $
by convention; see Example 3.6. We get that
![]() $S:= T_{\mathbf {u}}( \partial H)$
is a sphere separating
$S:= T_{\mathbf {u}}( \partial H)$
is a sphere separating
![]() $\{ \mathbf {v} \}$
and
$\{ \mathbf {v} \}$
and
![]() $\mathrm {cone}_{\mathbf {u}} \{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
such that
$\mathrm {cone}_{\mathbf {u}} \{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
such that
![]() $\mathbf {v} \not \in S $
and
$\mathbf {v} \not \in S $
and
![]() $\mathbf {u}, \mathbf {u} - \mathbf {u}^* \in S$
(since
$\mathbf {u}, \mathbf {u} - \mathbf {u}^* \in S$
(since
![]() $\mathbf {u} = T_{\mathbf {u}}(\infty )$
and
$\mathbf {u} = T_{\mathbf {u}}(\infty )$
and
![]() $ \mathbf {u} - \mathbf {u}^* = T_{\mathbf {u}}(\mathbf {0})$
). Let
$ \mathbf {u} - \mathbf {u}^* = T_{\mathbf {u}}(\mathbf {0})$
). Let
![]() $\alpha \langle \mathbf {z}, \mathbf {z} \rangle + \langle \mathbf {z}, \mathbf {a} \rangle + \beta = 0$
be the equation of S and choose the signs such that
$\alpha \langle \mathbf {z}, \mathbf {z} \rangle + \langle \mathbf {z}, \mathbf {a} \rangle + \beta = 0$
be the equation of S and choose the signs such that
![]() $\alpha \langle \mathbf {v}, \mathbf {v} \rangle + \langle {\mathbf {v}}, {\mathbf {v}} \rangle + \beta> 0$
. Since S is a separating sphere, we get that
$\alpha \langle \mathbf {v}, \mathbf {v} \rangle + \langle {\mathbf {v}}, {\mathbf {v}} \rangle + \beta> 0$
. Since S is a separating sphere, we get that
![]() $\alpha \langle \mathbf {z}_i, \mathbf {z}_i \rangle + \langle \mathbf {z}_i, \mathbf {a} \rangle + \beta \leq 0$
for all
$\alpha \langle \mathbf {z}_i, \mathbf {z}_i \rangle + \langle \mathbf {z}_i, \mathbf {a} \rangle + \beta \leq 0$
for all
![]() $i = 1, \ldots , k$
. Moreover, since S passes through
$i = 1, \ldots , k$
. Moreover, since S passes through
![]() $\mathbf {u}, \mathbf {u} - \mathbf {u}^*$
, we get
$\mathbf {u}, \mathbf {u} - \mathbf {u}^*$
, we get
 $$ \begin{align} \alpha \langle \mathbf{u}, \mathbf{u} \rangle + \langle \mathbf{u}, \mathbf{a} \rangle + \beta &= 0 \quad \mbox{ and } \\ \alpha \langle \mathbf{u} -\mathbf{u}^*, \mathbf{u} -\mathbf{u}^* \rangle + \langle \mathbf{u} - \mathbf{u}^*, \mathbf{a} \rangle + \beta &= 0. \nonumber \end{align} $$
$$ \begin{align} \alpha \langle \mathbf{u}, \mathbf{u} \rangle + \langle \mathbf{u}, \mathbf{a} \rangle + \beta &= 0 \quad \mbox{ and } \\ \alpha \langle \mathbf{u} -\mathbf{u}^*, \mathbf{u} -\mathbf{u}^* \rangle + \langle \mathbf{u} - \mathbf{u}^*, \mathbf{a} \rangle + \beta &= 0. \nonumber \end{align} $$
Simplifying the second equation and using (5.6) gives
or
![]() $2\alpha \langle \mathbf {u}, \mathbf {u} \rangle + \langle \mathbf {u}, \mathbf {a} \rangle - \alpha = 0$
. Subtracting (5.6), one obtains
$2\alpha \langle \mathbf {u}, \mathbf {u} \rangle + \langle \mathbf {u}, \mathbf {a} \rangle - \alpha = 0$
. Subtracting (5.6), one obtains
therefore concluding the proof.
Remark 5.8. The proof of Lemma 5.7 shows that when
![]() $\mathbf {u}=\infty $
, it reduces to the usual Farkas’ lemma; see Lemma 2.2.7 in [Reference Borwein and Lewis2].
$\mathbf {u}=\infty $
, it reduces to the usual Farkas’ lemma; see Lemma 2.2.7 in [Reference Borwein and Lewis2].
6 Polar convexity with multiple poles
Problems in polar convexity involving a single pole can often be reduced to the setting of classical convexity. However, as the examples above show, a set can be convex with respect to multiple poles at once. In this section, we look at how multiple poles interact with each other. We start by defining what a convex hull with respect to multiple poles is.
Definition 6.1 Given
![]() $U, Z \subseteq \hat {\mathbb {R}}^n$
, define the convex hull of Z with respect to U, denoted by
$U, Z \subseteq \hat {\mathbb {R}}^n$
, define the convex hull of Z with respect to U, denoted by
![]() $\mathrm {conv}_{U}(Z)$
, to be the smallest set in
$\mathrm {conv}_{U}(Z)$
, to be the smallest set in
![]() $\hat {\mathbb {R}}^n$
containing Z and convex with respect to each
$\hat {\mathbb {R}}^n$
containing Z and convex with respect to each
![]() $\mathbf {u} \in U$
.
$\mathbf {u} \in U$
.
If
![]() $U = \emptyset $
above, then
$U = \emptyset $
above, then
![]() $\mathrm {conv}_{U}(Z)$
is simply Z, and if
$\mathrm {conv}_{U}(Z)$
is simply Z, and if
![]() $Z = \emptyset $
, then
$Z = \emptyset $
, then
![]() $\mathrm {conv}_{U}(Z)$
is also
$\mathrm {conv}_{U}(Z)$
is also
![]() $\emptyset $
. Similar to (3.3), for
$\emptyset $
. Similar to (3.3), for
![]() $\mathbf {u} \in \mathbb {R}^n$
, we have
$\mathbf {u} \in \mathbb {R}^n$
, we have
It is natural to ask what the convex hull of a given set with respect to multiple poles looks like. For example, given poles
![]() $u, \infty $
and points
$u, \infty $
and points
![]() $z_1, z_2, z_3$
in the complex plane, their
$z_1, z_2, z_3$
in the complex plane, their
![]() $\{u, \infty \}$
-convex hull is displayed in Figure 3.
$\{u, \infty \}$
-convex hull is displayed in Figure 3.

Figure 3:
![]() $\mathrm {conv}_{\{u, \infty \}} \{z_1, z_2, z_3\}$
.
$\mathrm {conv}_{\{u, \infty \}} \{z_1, z_2, z_3\}$
.
We are going to prove an inductive procedure for finding the convex hull of a set, given finitely many poles. Before we do that, we recall the definition of a convex polytope.
Definition 6.2 (Convex polytope)
A convex polytope in
![]() $\mathbb {R}^n$
is the convex hull of a finite number of points in
$\mathbb {R}^n$
is the convex hull of a finite number of points in
![]() $\mathbb {R}^n$
. A face of a polytope is an intersection of the polytope with a hyperplane, such that none of the relative interior points lie in the hyperplane. Faces of a polytope are partially ordered by inclusion. Maximal faces are those that are not contained in any other face of the polytope. A polytope
$\mathbb {R}^n$
. A face of a polytope is an intersection of the polytope with a hyperplane, such that none of the relative interior points lie in the hyperplane. Faces of a polytope are partially ordered by inclusion. Maximal faces are those that are not contained in any other face of the polytope. A polytope
![]() $P \subset \mathbb {R}^n $
has full dimension if its real span is
$P \subset \mathbb {R}^n $
has full dimension if its real span is
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Definition 6.3 Given points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and a
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and a
![]() $\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the affine hull of
$\mathbf {u} \in \hat {\mathbb {R}}^n$
distinct from them, define the affine hull of
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to
$\mathbf {z}_1,\ldots , \mathbf {z}_k$
with respect to
![]() $\mathbf {u}$
to be
$\mathbf {u}$
to be
 $$ \begin{align*}\mathrm{aff}_{\mathbf{u}} \{ \mathbf{z}_1,\ldots , \mathbf{z}_k\} := \Big\{ \mathbf{u} +\Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* : t_i \in \mathbb{R} \text{ with } \sum _{i=1}^k t_i = 1 \Big\} \cup \{\mathbf{u}\}. \end{align*} $$
$$ \begin{align*}\mathrm{aff}_{\mathbf{u}} \{ \mathbf{z}_1,\ldots , \mathbf{z}_k\} := \Big\{ \mathbf{u} +\Big( \sum _{i=1}^k t_i (\mathbf{z}_i - \mathbf{u})^* \Big)^* : t_i \in \mathbb{R} \text{ with } \sum _{i=1}^k t_i = 1 \Big\} \cup \{\mathbf{u}\}. \end{align*} $$
If
![]() $\mathbf {u} \in \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \}$
, define
$\mathbf {u} \in \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \}$
, define
![]() $\mathrm {aff}_{\mathbf {u}} \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \} := \mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \not =\mathbf {u}, i=1,\ldots , k\}\cup \{\mathbf {u}\}$
.
$\mathrm {aff}_{\mathbf {u}} \{\mathbf {z}_1, \ldots ,\mathbf {z}_k \} := \mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \not =\mathbf {u}, i=1,\ldots , k\}\cup \{\mathbf {u}\}$
.
For example, the affine hull of one point is the union of the point and
![]() $\{\mathbf {u}\}$
. The affine hull of two distinct points is the unique circle (or line) passing through them and the pole
$\{\mathbf {u}\}$
. The affine hull of two distinct points is the unique circle (or line) passing through them and the pole
![]() $\mathbf {u}$
, including
$\mathbf {u}$
, including
![]() $\mathbf {u}$
. The affine hull of three distinct points is either a circle, if they together with
$\mathbf {u}$
. The affine hull of three distinct points is either a circle, if they together with
![]() $\mathbf {u}$
are on a circle, or a two-dimensional sphere (or affine space), otherwise.
$\mathbf {u}$
are on a circle, or a two-dimensional sphere (or affine space), otherwise.
Using Definition 3.2, one can see that
![]() $\mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
is the generalized
$\mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
is the generalized
![]() $\ell $
-sphere, with the smallest
$\ell $
-sphere, with the smallest
![]() $\ell $
, that contains
$\ell $
, that contains
![]() $\mathbf {z}_1,\ldots , \mathbf {z}_k$
and
$\mathbf {z}_1,\ldots , \mathbf {z}_k$
and
![]() $\mathbf {u}$
. When
$\mathbf {u}$
. When
![]() $\mathbf {u} = \infty $
, then
$\mathbf {u} = \infty $
, then
![]() $\mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
becomes the affine space, spanned by
$\mathrm {aff}_{\mathbf {u}} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
becomes the affine space, spanned by
![]() $\{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
over
$\{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
over
![]() $\mathbb {R}$
. We denote the latter simply by
$\mathbb {R}$
. We denote the latter simply by
![]() $\mathrm {aff} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
.
$\mathrm {aff} \{ \mathbf {z}_1,\ldots , \mathbf {z}_k\}$
.
Lemma 6.1 Let
![]() $\mathbf {u}, \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, such that
$\mathbf {u}, \mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct, such that
![]() $\mathrm {conv}_u \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
has nonempty interior. Consider the family
$\mathrm {conv}_u \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
has nonempty interior. Consider the family
 $$ \begin{align*} \mathcal{L} : = \big\{ S \subset \hat{\mathbb{R}}^n : S\ \mathrm{closed\ spherical\ domain, } &\{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} \subset S, \mathbf{u} \in \partial S \\ &\mathrm{\,and }\ \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \} = \partial S \big\}. \end{align*} $$
$$ \begin{align*} \mathcal{L} : = \big\{ S \subset \hat{\mathbb{R}}^n : S\ \mathrm{closed\ spherical\ domain, } &\{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} \subset S, \mathbf{u} \in \partial S \\ &\mathrm{\,and }\ \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \} = \partial S \big\}. \end{align*} $$
Then,
![]() $\mathcal {L}$
is finite, and we have
$\mathcal {L}$
is finite, and we have
and
Proof Without loss of generality, we may assume
![]() $\mathbf {u} = \infty $
. Then,
$\mathbf {u} = \infty $
. Then,
![]() $\mathrm {conv}\{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
is a convex polytope of full dimension and can be written as the intersection of supporting half-spaces corresponding to each of its maximal faces. Since the polytope
$\mathrm {conv}\{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
is a convex polytope of full dimension and can be written as the intersection of supporting half-spaces corresponding to each of its maximal faces. Since the polytope
![]() $\mathrm {conv}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is of full dimension, there are clearly only finitely many half-spaces H, such that
$\mathrm {conv}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
is of full dimension, there are clearly only finitely many half-spaces H, such that
![]() $\mbox {aff}\{\{\mathbf {z}_1 ,\ldots , \mathbf {z}_k \} \cap \partial H \}$
is a hyperplane. The second statement now follows from Remark 2.4.
$\mbox {aff}\{\{\mathbf {z}_1 ,\ldots , \mathbf {z}_k \} \cap \partial H \}$
is a hyperplane. The second statement now follows from Remark 2.4.
Remark 6.2. Notice that the set
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
has empty interior if and only if the polytope
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
has empty interior if and only if the polytope
![]() $\mathrm {conv}\{ T_{\mathbf {u}} (\mathbf {z}_1 ) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) \}$
is not a full dimensional polytope. This happens when the points
$\mathrm {conv}\{ T_{\mathbf {u}} (\mathbf {z}_1 ) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) \}$
is not a full dimensional polytope. This happens when the points
![]() $T_{\mathbf {u}} (\mathbf {z}_1 ) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) $
all lie in a hyperplane – that is, when
$T_{\mathbf {u}} (\mathbf {z}_1 ) , \ldots , T_{\mathbf {u}} (\mathbf {z}_k ) $
all lie in a hyperplane – that is, when
![]() $\mbox {aff}\{ T_{\mathbf {u}}(\mathbf {z}_1) ,\ldots , T_{\mathbf {u}}(\mathbf {z}_k )\} $
is not the full space. This is equivalent to saying that
$\mbox {aff}\{ T_{\mathbf {u}}(\mathbf {z}_1) ,\ldots , T_{\mathbf {u}}(\mathbf {z}_k )\} $
is not the full space. This is equivalent to saying that
![]() $\mbox {aff}_{\mathbf {u}} \{\mathbf {z}_1 ,\ldots , \mathbf {z}_k \} $
is not the full space or that the points
$\mbox {aff}_{\mathbf {u}} \{\mathbf {z}_1 ,\ldots , \mathbf {z}_k \} $
is not the full space or that the points
![]() $\mathbf {u} , \mathbf {z}_1 , \ldots , \mathbf {z}_k$
all lie on a
$\mathbf {u} , \mathbf {z}_1 , \ldots , \mathbf {z}_k$
all lie on a
![]() $(n - 1)$
-sphere.
$(n - 1)$
-sphere.
Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
![]() $\mathbf {u}_1 , \mathbf {u}_2 \in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
$\mathbf {u}_1 , \mathbf {u}_2 \in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
). For
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
). For
![]() $i \in \{ 1, 2\}$
, consider the following two families of spherical domains:
$i \in \{ 1, 2\}$
, consider the following two families of spherical domains:
 $$ \begin{align} \mathcal{S}_i : = \big\{ S \subset \hat{\mathbb{R}}^n : S \mbox{ closed spherical domain, } &\{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} \subset S, \\ &\mathbf{u}_i \in \partial S \mbox{ and } \{ \mathbf{u}_1 , \mathbf{u}_2 \} \subset \mathrm{cl}(S^c) \} \nonumber \end{align} $$
$$ \begin{align} \mathcal{S}_i : = \big\{ S \subset \hat{\mathbb{R}}^n : S \mbox{ closed spherical domain, } &\{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} \subset S, \\ &\mathbf{u}_i \in \partial S \mbox{ and } \{ \mathbf{u}_1 , \mathbf{u}_2 \} \subset \mathrm{cl}(S^c) \} \nonumber \end{align} $$
and
Note that these families contain domains that are convex with respect to both
![]() $\mathbf {u}_1$
and
$\mathbf {u}_1$
and
![]() $\mathbf {u}_2$
. Also note that
$\mathbf {u}_2$
. Also note that
![]() $\mathcal {L}_i$
is necessarily a finite set. With that in mind, we have the following result. Its proof can be found in the appendix.
$\mathcal {L}_i$
is necessarily a finite set. With that in mind, we have the following result. Its proof can be found in the appendix.
Theorem 6.3 Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
![]() $\mathbf {u}_1, \mathbf {u}_2\in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
$\mathbf {u}_1, \mathbf {u}_2\in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
). Suppose that not all of
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
). Suppose that not all of
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a
![]() $(n - 1)\mbox {-sphere}$
. Then,
$(n - 1)\mbox {-sphere}$
. Then,
 $$ \begin{align} \mathrm{conv}_{\mathbf{u}_2} (\mathrm{conv}_{\mathbf{u}_1} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} ) = \bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S, \end{align} $$
$$ \begin{align} \mathrm{conv}_{\mathbf{u}_2} (\mathrm{conv}_{\mathbf{u}_1} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \} ) = \bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S, \end{align} $$
where
![]() $\mathcal {S}_i$
,
$\mathcal {S}_i$
,
![]() $i=1,2$
, are the families of closed spherical domains defined in (6.1).
$i=1,2$
, are the families of closed spherical domains defined in (6.1).
As a consequence of the above, we have the following convenient fact.
Corollary 6.4 For any distinct
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and
$\mathbf {z}_1 , \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
and
![]() $\mathbf {u}_1, \mathbf {u}_2 \in \hat {\mathbb {R}}^n $
not necessarily distinct from
$\mathbf {u}_1, \mathbf {u}_2 \in \hat {\mathbb {R}}^n $
not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
, we have
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
, we have
 $$ \begin{align} \mathrm{conv}_{\{\mathbf{u}_1 , \mathbf{u}_2\}}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} &= \mathrm{conv}_{\mathbf{u}_1}(\mathrm{conv}_{\mathbf{u}_2}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \}) \\ &= \mathrm{conv}_{\mathbf{u}_2}(\mathrm{conv}_{\mathbf{u}_1}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \}). \nonumber \end{align} $$
$$ \begin{align} \mathrm{conv}_{\{\mathbf{u}_1 , \mathbf{u}_2\}}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \} &= \mathrm{conv}_{\mathbf{u}_1}(\mathrm{conv}_{\mathbf{u}_2}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \}) \\ &= \mathrm{conv}_{\mathbf{u}_2}(\mathrm{conv}_{\mathbf{u}_1}\{\mathbf{z}_1 , \ldots , \mathbf{z}_k \}). \nonumber \end{align} $$
Proof Without loss of generality, assume
![]() $\mathbf {u}_1 = \infty $
. If
$\mathbf {u}_1 = \infty $
. If
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \cup \{ \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a hyperplane, the sets in (6.4) will also all lie in this hyperplane. So we can restrict to this hyperplane to assume that not all of
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \cup \{ \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a hyperplane, the sets in (6.4) will also all lie in this hyperplane. So we can restrict to this hyperplane to assume that not all of
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \cup \{ \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a hyperplane. We prove the first equality; the second follows by symmetry. The containment
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \cup \{ \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a hyperplane. We prove the first equality; the second follows by symmetry. The containment
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) \subseteq \mathrm {conv}_{\{\mathbf {u}_1 , \mathbf {u}_2\}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
follows from minimality in Definition 6.1. We want to show the opposite inclusion
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) \subseteq \mathrm {conv}_{\{\mathbf {u}_1 , \mathbf {u}_2\}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
follows from minimality in Definition 6.1. We want to show the opposite inclusion
From Theorem 6.3, we see that
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) = \bigcap _{i=1}^2 \bigcap _{S\in \mathcal {S}_i} S$
. All the domains S lying in either
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) = \bigcap _{i=1}^2 \bigcap _{S\in \mathcal {S}_i} S$
. All the domains S lying in either
![]() $\mathcal {S}_1$
or
$\mathcal {S}_1$
or
![]() $\mathcal {S}_2$
are convex with respect to both
$\mathcal {S}_2$
are convex with respect to both
![]() $\mathbf {u}_1$
and
$\mathbf {u}_1$
and
![]() $\mathbf {u}_2$
by definition. It follows that
$\mathbf {u}_2$
by definition. It follows that
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is also convex with respect to both
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is also convex with respect to both
![]() $\mathbf {u}_1$
and
$\mathbf {u}_1$
and
![]() $\mathbf {u}_2$
. Again by minimality in Definition 6.1, we get that
$\mathbf {u}_2$
. Again by minimality in Definition 6.1, we get that
completing the proof.
Corollary 6.5 For any
![]() $Z \subset \hat {\mathbb {R}}^n$
and distinct
$Z \subset \hat {\mathbb {R}}^n$
and distinct
![]() $\mathbf {u}_1 , \mathbf {u}_2 \in \hat {\mathbb {R}}^n$
, we have
$\mathbf {u}_1 , \mathbf {u}_2 \in \hat {\mathbb {R}}^n$
, we have
Proof We prove the first equality; the other one follows by symmetry. The inclusion
follows by minimality. To see the other inclusion, it is sufficient to prove that
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
is
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
is
![]() $\mathbf {u}_2$
-convex. Let
$\mathbf {u}_2$
-convex. Let
![]() $\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
. Then, by repeated application of Carathéodory’s theorem, we get
$\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
. Then, by repeated application of Carathéodory’s theorem, we get
![]() $\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}\{ \mathbf {v}_1 , \ldots , \mathbf {v}_\ell \}$
for some
$\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}\{ \mathbf {v}_1 , \ldots , \mathbf {v}_\ell \}$
for some
![]() $\mathbf {v}_1 , \ldots , \mathbf {v}_\ell \in \mathrm {conv}_{\mathbf {u}_2}(Z)$
. By Carathéodory’s theorem again, we get that
$\mathbf {v}_1 , \ldots , \mathbf {v}_\ell \in \mathrm {conv}_{\mathbf {u}_2}(Z)$
. By Carathéodory’s theorem again, we get that
![]() $\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \})$
for some
$\mathbf {x}_1 , \mathbf {x}_2 \in \mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \})$
for some
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k \in Z$
, that may be assumed distinct. By Corollary 6.4,
$\mathbf {z}_1 , \ldots , \mathbf {z}_k \in Z$
, that may be assumed distinct. By Corollary 6.4,
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \})$
is
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \})$
is
![]() $\mathbf {u}_2$
-convex, so
$\mathbf {u}_2$
-convex, so
Therefore, the set
![]() $\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
is convex with respect to both
$\mathrm {conv}_{\mathbf {u}_1}(\mathrm {conv}_{\mathbf {u}_2}(Z))$
is convex with respect to both
![]() $\mathbf {u}_1$
and
$\mathbf {u}_1$
and
![]() $\mathbf {u}_2$
and contains Z. So, by minimality,
$\mathbf {u}_2$
and contains Z. So, by minimality,
concluding the proof.
Corollary 6.6 Given
![]() $Z \subseteq \hat {\mathbb {R}}^n$
and distinct points
$Z \subseteq \hat {\mathbb {R}}^n$
and distinct points
![]() $\mathbf {u}_1, \ldots , \mathbf {u}_m$
in
$\mathbf {u}_1, \ldots , \mathbf {u}_m$
in
![]() $\hat {\mathbb {R}}^n$
, we have
$\hat {\mathbb {R}}^n$
, we have
Moreover, the polar convex hull on the left does not depend on the order in which we take the polar convex hulls on the right.
Proof As before, by minimality, we have the following inclusion:
So it is enough to prove that
![]() $\mathrm {conv}_{\mathbf {u}_m}(\mathrm {conv}_{\{\mathbf {u}_1, \ldots , \mathbf {u}_{m-1}\}}(Z)) $
is convex with respect to all of
$\mathrm {conv}_{\mathbf {u}_m}(\mathrm {conv}_{\{\mathbf {u}_1, \ldots , \mathbf {u}_{m-1}\}}(Z)) $
is convex with respect to all of
![]() $\mathbf {u}_i$
,
$\mathbf {u}_i$
,
![]() $i=1 , \ldots , m$
. We use induction on the number of poles, m. Note that the base case,
$i=1 , \ldots , m$
. We use induction on the number of poles, m. Note that the base case,
![]() $m=2$
, is Corollary 6.5. Assume the corollary to be true for
$m=2$
, is Corollary 6.5. Assume the corollary to be true for
![]() $m-1$
poles. Then, by the induction hypothesis
$m-1$
poles. Then, by the induction hypothesis
Taking the
![]() $\mathbf {u}_m$
convex hull and using Corollary 6.5, we get
$\mathbf {u}_m$
convex hull and using Corollary 6.5, we get
 $$ \begin{align*} \mbox{conv}_{\mathbf{u}_m} (\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-1}\} } (Z)) &= \mbox{conv}_{\mathbf{u}_m}(\mbox{conv}_{\mathbf{u}_{m-1}}(\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-2}\} } (Z))) \\ &= \mbox{conv}_{\mathbf{u}_{m-1}}(\mbox{conv}_{\mathbf{u}_m}(\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-2}\} } (Z))). \end{align*} $$
$$ \begin{align*} \mbox{conv}_{\mathbf{u}_m} (\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-1}\} } (Z)) &= \mbox{conv}_{\mathbf{u}_m}(\mbox{conv}_{\mathbf{u}_{m-1}}(\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-2}\} } (Z))) \\ &= \mbox{conv}_{\mathbf{u}_{m-1}}(\mbox{conv}_{\mathbf{u}_m}(\mbox{conv}_{ \{ \mathbf{u}_1, \ldots , \mathbf{u}_{m-2}\} } (Z))). \end{align*} $$
By a similar reasoning, we may replace
![]() $\mathbf {u}_{m-1}$
by any other
$\mathbf {u}_{m-1}$
by any other
![]() $\mathbf {u}_i$
for
$\mathbf {u}_i$
for
![]() ${i = 1, \ldots , m-1}$
. Therefore, we conclude that
${i = 1, \ldots , m-1}$
. Therefore, we conclude that
![]() $\mathrm {conv}_{\mathbf {u}_m}(\mathrm {conv}_{\{\mathbf {u}_1, \ldots , \mathbf {u}_{m-1}\}}(Z)) $
is indeed convex with respect to all the
$\mathrm {conv}_{\mathbf {u}_m}(\mathrm {conv}_{\{\mathbf {u}_1, \ldots , \mathbf {u}_{m-1}\}}(Z)) $
is indeed convex with respect to all the
![]() $\mathbf {u}_i$
’s, so the corollary holds.
$\mathbf {u}_i$
’s, so the corollary holds.
Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
![]() $\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
$\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
). To shorten the notation in the proof of the next theorem, we define
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
). To shorten the notation in the proof of the next theorem, we define
Analogous to the families considered in (6.2), we consider the following families of spherical domains, for
![]() $i \in \{ 1, \ldots , m\}$
:
$i \in \{ 1, \ldots , m\}$
:
 $$ \begin{align} \mathcal{L}_i : = \big\{ S \subset \hat{\mathbb{R}}^n : S \mbox{ closed } &\mbox{spherical domain, } Z_k \subset S, \, \mathbf{u}_i \in \partial S \mbox{ and } \\ & U_m \subset \mathrm{cl}(S^c) \mbox{ and } \mathrm{aff}_{\mathbf{u}_i} \{ (Z_k \cup U_m) \cap \partial S \} = \partial S \}. \nonumber \end{align} $$
$$ \begin{align} \mathcal{L}_i : = \big\{ S \subset \hat{\mathbb{R}}^n : S \mbox{ closed } &\mbox{spherical domain, } Z_k \subset S, \, \mathbf{u}_i \in \partial S \mbox{ and } \\ & U_m \subset \mathrm{cl}(S^c) \mbox{ and } \mathrm{aff}_{\mathbf{u}_i} \{ (Z_k \cup U_m) \cap \partial S \} = \partial S \}. \nonumber \end{align} $$
In words, the domains in
![]() $\mathcal {L}_i$
are
$\mathcal {L}_i$
are
![]() $\mathbf {u}_j$
-convex, for all
$\mathbf {u}_j$
-convex, for all
![]() $j=1,\ldots , m$
, with the additional requirement that
$j=1,\ldots , m$
, with the additional requirement that
![]() $\mathbf {u}_i \in \partial S$
. Moreover, the domains in
$\mathbf {u}_i \in \partial S$
. Moreover, the domains in
![]() $\mathcal {L}_i$
are determined by some of the points
$\mathcal {L}_i$
are determined by some of the points
![]() $ Z_k \cup U_m$
.
$ Z_k \cup U_m$
.
Theorem 6.7 Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
,
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
,
![]() $n \ge 2$
, be distinct and let the points
$n \ge 2$
, be distinct and let the points
![]() $\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
,
$\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
,
![]() $m \geq 2$
, be distinct (but not necessarily distinct from
$m \geq 2$
, be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
), such that
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
), such that
![]() $\mathrm {conv}_{U_m} (Z_k)$
has nonempty interior. Then the boundary of
$\mathrm {conv}_{U_m} (Z_k)$
has nonempty interior. Then the boundary of
![]() $\mathrm {conv}_{ U_m}(Z_k)$
is made up of pieces of the boundaries of closed spherical domains S with the following properties:
$\mathrm {conv}_{ U_m}(Z_k)$
is made up of pieces of the boundaries of closed spherical domains S with the following properties:
-
(a) Each S lies in
 $\mathcal {L}_i$
, for some
$\mathcal {L}_i$
, for some
 $i = 1 , \ldots , m$
,
$i = 1 , \ldots , m$
, -
(b) Each piece of the boundary is of the form
 $\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k)$
, and
$\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k)$
, and -
(c) We have
(6.6)In other words, given a point $$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{S \in \mathcal{L}_i} S. \end{align} $$
$$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{S \in \mathcal{L}_i} S. \end{align} $$
 $\mathbf {z} \not \in \mathrm {conv}_{ U_m }(Z_k)$
, there exists a spherical domain
$\mathbf {z} \not \in \mathrm {conv}_{ U_m }(Z_k)$
, there exists a spherical domain
 $S \in \mathcal {L}_i$
, such that
$S \in \mathcal {L}_i$
, such that
 $\mathbf {z} \not \in S$
, for some
$\mathbf {z} \not \in S$
, for some
 $i = 1, \ldots , m$
.
$i = 1, \ldots , m$
.
Proof If
![]() $\mathrm {conv}_{ U_m}(Z_k)$
is the entire
$\mathrm {conv}_{ U_m}(Z_k)$
is the entire
![]() $\hat {\mathbb {R}}^n$
, then the families
$\hat {\mathbb {R}}^n$
, then the families
![]() $\mathcal {L}_i$
are empty and the theorem holds, so assume that this is not the case. The proof is by an induction on the dimension of the ambient space, n. When the dimension is
$\mathcal {L}_i$
are empty and the theorem holds, so assume that this is not the case. The proof is by an induction on the dimension of the ambient space, n. When the dimension is
![]() $n = 2$
, the theorem is simply [Reference Sendov, Sendov and Wang11, Theorem 5.2]. Suppose that
$n = 2$
, the theorem is simply [Reference Sendov, Sendov and Wang11, Theorem 5.2]. Suppose that
![]() $n \ge 3$
and the result holds when the dimension of the space is
$n \ge 3$
and the result holds when the dimension of the space is
![]() $n-1$
or lower. This assumption means that the result holds in any subspace or affine space of
$n-1$
or lower. This assumption means that the result holds in any subspace or affine space of
![]() $\hat {\mathbb {R}}^n$
of dimension
$\hat {\mathbb {R}}^n$
of dimension
![]() $n-1$
or on any sphere in
$n-1$
or on any sphere in
![]() $\hat {\mathbb {R}}^n$
of dimension
$\hat {\mathbb {R}}^n$
of dimension
![]() $n-1$
. To see the latter, simply send a point of the said sphere to
$n-1$
. To see the latter, simply send a point of the said sphere to
![]() $\infty $
using a Möbius transformation.
$\infty $
using a Möbius transformation.
We begin with the following containments:
 $$ \begin{align} \bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S, \end{align} $$
$$ \begin{align} \bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S, \end{align} $$
where the inclusions follow by the minimality of the convex hulls. To conclude the proof, it is sufficient to show that
 $$ \begin{align} \bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) = \partial \Big( \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \Big). \end{align} $$
$$ \begin{align} \bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) = \partial \Big( \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \Big). \end{align} $$
Indeed, assume (6.8) holds. Without loss of generality, assume that
![]() $\mathbf {u}_m = \infty $
or else apply a Möbius transformation to
$\mathbf {u}_m = \infty $
or else apply a Möbius transformation to
![]() $\hat {\mathbb {R}}^n$
that sends
$\hat {\mathbb {R}}^n$
that sends
![]() $\mathbf {u}_m$
to
$\mathbf {u}_m$
to
![]() $\infty $
. Then,
$\infty $
. Then,
![]() $\bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
is a closed convex set, and so it is equal to the convex hull of its boundary. Taking the convex hull of all parts in (6.7), we have
$\bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
is a closed convex set, and so it is equal to the convex hull of its boundary. Taking the convex hull of all parts in (6.7), we have
 $$ \begin{align*} \mathrm{conv} &\Big(\bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m } (\partial S \cap Z_k ) \Big) \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \\ &= \mathrm{conv} \Big( \partial \Big( \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \Big) \Big) = \mathrm{conv} \Big(\bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) \Big). \end{align*} $$
$$ \begin{align*} \mathrm{conv} &\Big(\bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m } (\partial S \cap Z_k ) \Big) \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \\ &= \mathrm{conv} \Big( \partial \Big( \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S \Big) \Big) = \mathrm{conv} \Big(\bigcup_{\substack{S \in \mathcal{L}_j \\ j=1,\ldots, m}} \mathrm{conv}_{\partial S \cap U_m} (\partial S \cap Z_k ) \Big). \end{align*} $$
Thus, we have equalities throughout, and we are done.
For the remainder of the proof, we show (6.8). Since
![]() $ \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
is the intersection of spherical domains, the boundaries of such domains are the sole contributors to the boundary of
$ \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
is the intersection of spherical domains, the boundaries of such domains are the sole contributors to the boundary of
![]() $ \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S $
. To see that each domain S contributes exactly a piece of the form
$ \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S $
. To see that each domain S contributes exactly a piece of the form
![]() $\mathrm {conv}_{\partial S \cap U_m} (\partial S \cap Z_k)$
, fix some
$\mathrm {conv}_{\partial S \cap U_m} (\partial S \cap Z_k)$
, fix some
![]() $S \in \mathcal {L}_i$
and restrict to its boundary
$S \in \mathcal {L}_i$
and restrict to its boundary
![]() $\partial S$
. Let
$\partial S$
. Let
Recalling Definition 3.3, define the following families of spherical domains:
 $$ \begin{align*} \mathcal{L}_j^{\prime} : = \big\{ S' \subset \partial S &: S' \mbox{ closed spherical domain, } \partial S \cap Z_k \subset S', \mathbf{u}_j^{\prime} \in \partial S', \\ &\partial S \cap U_m \subset \mathrm{cl}(S^{\prime c}) \mbox{ and } \mathrm{aff}_{\mathbf{u}_j^{\prime}} \{ \partial S \cap (Z_k \cup U_m) \cap \partial S' \} = \partial S' \big\}, \end{align*} $$
$$ \begin{align*} \mathcal{L}_j^{\prime} : = \big\{ S' \subset \partial S &: S' \mbox{ closed spherical domain, } \partial S \cap Z_k \subset S', \mathbf{u}_j^{\prime} \in \partial S', \\ &\partial S \cap U_m \subset \mathrm{cl}(S^{\prime c}) \mbox{ and } \mathrm{aff}_{\mathbf{u}_j^{\prime}} \{ \partial S \cap (Z_k \cup U_m) \cap \partial S' \} = \partial S' \big\}, \end{align*} $$
where in this definition, by
![]() $\partial S'$
, we understand the boundary of
$\partial S'$
, we understand the boundary of
![]() $S'$
relative to
$S'$
relative to
![]() $\partial S$
, and by
$\partial S$
, and by
![]() $S^{\prime c}$
, we understand the complement of
$S^{\prime c}$
, we understand the complement of
![]() $S'$
relative to
$S'$
relative to
![]() $\partial S$
.
$\partial S$
.
Since
![]() $\partial S$
is a dimension
$\partial S$
is a dimension
![]() $n -1 $
ambient space, the theorem holds by the induction hypothesis, so
$n -1 $
ambient space, the theorem holds by the induction hypothesis, so
 $$ \begin{align} \mathrm{conv}_{\partial S \cap U_m } (\partial S \cap Z_k) = \bigcap_{j=1}^{m'} \bigcap_{S' \in \mathcal{L}_j^{\prime}} S'. \end{align} $$
$$ \begin{align} \mathrm{conv}_{\partial S \cap U_m } (\partial S \cap Z_k) = \bigcap_{j=1}^{m'} \bigcap_{S' \in \mathcal{L}_j^{\prime}} S'. \end{align} $$
In the next two paragraphs, we explain how each domain
![]() $S' \in \mathcal {L}_j^{\prime }$
can be extended to a domain
$S' \in \mathcal {L}_j^{\prime }$
can be extended to a domain
![]() $S" \in \mathcal {L}_j$
, such that
$S" \in \mathcal {L}_j$
, such that
![]() $S" \cap \partial S = S'$
. Without loss of generality, we may assume that both
$S" \cap \partial S = S'$
. Without loss of generality, we may assume that both
![]() $\mathcal {L}_j^{\prime }$
and
$\mathcal {L}_j^{\prime }$
and
![]() $\mathcal {L}_j$
correspond to the same pole
$\mathcal {L}_j$
correspond to the same pole
![]() $\mathbf {u}_j$
; that is,
$\mathbf {u}_j$
; that is,
![]() $\mathbf {u}_j^{\prime } = \mathbf {u}_j$
for
$\mathbf {u}_j^{\prime } = \mathbf {u}_j$
for
![]() $j=1,\ldots , m'$
(or else we just relabel
$j=1,\ldots , m'$
(or else we just relabel
![]() $\mathbf {u}_1,\ldots , \mathbf {u}_m$
so that
$\mathbf {u}_1,\ldots , \mathbf {u}_m$
so that
![]() $\mathbf {u}^{\prime }_1,\ldots , \mathbf {u}^{\prime }_{m'}$
are the first
$\mathbf {u}^{\prime }_1,\ldots , \mathbf {u}^{\prime }_{m'}$
are the first
![]() $m'$
of them).
$m'$
of them).
If
![]() $\mathcal {L}_j^{\prime }$
are all empty, then
$\mathcal {L}_j^{\prime }$
are all empty, then
![]() $\bigcap _{j=1}^{m'} \bigcap _{S' \in \mathcal {L}_j^{\prime }} S' = \partial S$
. So, (6.9) becomes
$\bigcap _{j=1}^{m'} \bigcap _{S' \in \mathcal {L}_j^{\prime }} S' = \partial S$
. So, (6.9) becomes
![]() $\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k) = \partial S$
, and then, (6.7) shows that
$\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k) = \partial S$
, and then, (6.7) shows that
 $$ \begin{align*}\partial S \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S. \end{align*} $$
$$ \begin{align*}\partial S \subseteq \mathrm{conv}_{ U_m }(Z_k) \subseteq \bigcap_{j=1}^{m} \bigcap_{S \in \mathcal{L}_j} S. \end{align*} $$
In this case, since there is at least one point in
![]() $U_m \cup Z_k$
not lying on
$U_m \cup Z_k$
not lying on
![]() $\partial S$
, and
$\partial S$
, and
![]() $S \in \mathcal {L}_i$
implies that
$S \in \mathcal {L}_i$
implies that
![]() $\mathrm {aff}_{\mathbf {u}_i} \{ (Z_k \cup U_m) \cap \partial S \} = \partial S$
, we conclude that
$\mathrm {aff}_{\mathbf {u}_i} \{ (Z_k \cup U_m) \cap \partial S \} = \partial S$
, we conclude that
![]() $\mathrm {conv}_{ U_m}(Z_k) = S$
. If
$\mathrm {conv}_{ U_m}(Z_k) = S$
. If
![]() $\mathcal {L}_j^{\prime }$
are not all empty, then fix
$\mathcal {L}_j^{\prime }$
are not all empty, then fix
![]() $S' \in \mathcal {L}_j^{\prime }$
and assume that
$S' \in \mathcal {L}_j^{\prime }$
and assume that
![]() $\mathbf {u}_j = \infty $
or else apply a Möbius transformation to
$\mathbf {u}_j = \infty $
or else apply a Möbius transformation to
![]() $\hat {\mathbb {R}}^n$
that sends
$\hat {\mathbb {R}}^n$
that sends
![]() $\mathbf {u}_j$
to
$\mathbf {u}_j$
to
![]() $\infty $
. (Abusing notation, we keep the names S and
$\infty $
. (Abusing notation, we keep the names S and
![]() $S'$
after that transformation.) Since
$S'$
after that transformation.) Since
![]() $\mathbf {u}_j \in \partial S' \subset \partial S$
,
$\mathbf {u}_j \in \partial S' \subset \partial S$
,
![]() $\partial S'$
becomes a hyperplane in
$\partial S'$
becomes a hyperplane in
![]() $\partial S$
, which is our ambient space of dimension
$\partial S$
, which is our ambient space of dimension
![]() $n-1$
. (Note that
$n-1$
. (Note that
![]() $\partial S$
becomes a hyperplane in
$\partial S$
becomes a hyperplane in
![]() $\hat {\mathbb {R}}^n$
.) By definition,
$\hat {\mathbb {R}}^n$
.) By definition,
![]() $S'$
contains the points
$S'$
contains the points
![]() $\partial S \cap Z_k$
and separates them from the points
$\partial S \cap Z_k$
and separates them from the points
![]() $\partial S \cap U_m $
, relative to
$\partial S \cap U_m $
, relative to
![]() $\partial S$
. Since
$\partial S$
. Since
![]() $\partial S$
separates
$\partial S$
separates
![]() $Z_k$
and
$Z_k$
and
![]() $U_m$
, the points
$U_m$
, the points
![]() $Z_k \setminus \partial S$
and
$Z_k \setminus \partial S$
and
![]() $U_m \setminus \partial S$
are strictly on different sides of
$U_m \setminus \partial S$
are strictly on different sides of
![]() $\partial S$
. Thus,
$\partial S$
. Thus,
![]() $S'$
can be extended to a half-space H in
$S'$
can be extended to a half-space H in
![]() $\hat {\mathbb {R}}^n$
that contains the points
$\hat {\mathbb {R}}^n$
that contains the points
![]() $Z_k$
and separates them from the points
$Z_k$
and separates them from the points
![]() $U_m$
. (To obtain this initial half space H, just rotate slightly the half-space S around
$U_m$
. (To obtain this initial half space H, just rotate slightly the half-space S around
![]() $\partial S'$
.) That is, the half-space H is such that
$\partial S'$
.) That is, the half-space H is such that
We show now that H can be chosen in such a way that
In this way, we have
![]() $H \in \mathcal {L}_j$
, and by construction,
$H \in \mathcal {L}_j$
, and by construction,
![]() $H \cap \partial S = S'$
.
$H \cap \partial S = S'$
.
If
![]() $\mathrm {dim\;} \mathrm {aff}_{\mathbf {u}_j} \{(Z_k\cup U_m) \cap \partial H\} = n-1$
, then we are done. So assume
$\mathrm {dim\;} \mathrm {aff}_{\mathbf {u}_j} \{(Z_k\cup U_m) \cap \partial H\} = n-1$
, then we are done. So assume
Since
![]() $ \partial S \cap (Z_k\cup U_m) \cap \partial S' \subseteq (Z_k\cup U_m) \cap \partial H$
, we have that
$ \partial S \cap (Z_k\cup U_m) \cap \partial S' \subseteq (Z_k\cup U_m) \cap \partial H$
, we have that
But the dimension of
![]() $\partial S'$
is
$\partial S'$
is
![]() $n-2$
, so we conclude that
$n-2$
, so we conclude that
and (6.10) holds with equality. Rotate
![]() $\partial H$
around
$\partial H$
around
![]() $\partial S'$
until it hits a point in
$\partial S'$
until it hits a point in
![]() $(Z_k\cup U_m) \smallsetminus \partial S$
. (Note that the latter set difference is not empty since otherwise,
$(Z_k\cup U_m) \smallsetminus \partial S$
. (Note that the latter set difference is not empty since otherwise,
![]() $\mathrm {conv}_{ U_m }(Z_k) \subset \partial S$
, contradicting the assumption that the polar convex hull has nonempty interior.) It should be clear now that after the rotation, the dimension of
$\mathrm {conv}_{ U_m }(Z_k) \subset \partial S$
, contradicting the assumption that the polar convex hull has nonempty interior.) It should be clear now that after the rotation, the dimension of
![]() $\mathrm {aff}_{\mathbf {u}_j} \{(Z_k\cup U_m) \cap \partial H\}$
is
$\mathrm {aff}_{\mathbf {u}_j} \{(Z_k\cup U_m) \cap \partial H\}$
is
![]() $n-1$
. Finally, let
$n-1$
. Finally, let
![]() $S"$
be the inverse image of H under the Möbius transformation that sent
$S"$
be the inverse image of H under the Möbius transformation that sent
![]() $\mathbf {u}_j$
to
$\mathbf {u}_j$
to
![]() $\infty $
.
$\infty $
.
By (6.9), we have that for each point
![]() $\mathbf {x} \in \partial S$
outside of
$\mathbf {x} \in \partial S$
outside of
![]() $\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k )$
, there is a spherical domain
$\mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k )$
, there is a spherical domain
![]() $S' \in \mathcal {L}_j^{\prime }$
, for some
$S' \in \mathcal {L}_j^{\prime }$
, for some
![]() $j=1,\ldots , m$
, that excludes
$j=1,\ldots , m$
, that excludes
![]() $\mathbf {x}$
, relative to
$\mathbf {x}$
, relative to
![]() $\partial S$
. By the above,
$\partial S$
. By the above,
![]() $S'$
can be extended to an
$S'$
can be extended to an
![]() $S" \in \mathcal {L}_j$
that satisfies
$S" \in \mathcal {L}_j$
that satisfies
![]() $S" \cap \partial S = S'$
, and hence,
$S" \cap \partial S = S'$
, and hence,
![]() $S"$
excludes
$S"$
excludes
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
Returning to (6.8), take a point
![]() $\mathbf {x} \in \partial \big ( \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S \big )$
. There is an
$\mathbf {x} \in \partial \big ( \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S \big )$
. There is an
![]() $S \in \mathcal {L}_i$
for some
$S \in \mathcal {L}_i$
for some
![]() $i=1,\ldots , m$
such that
$i=1,\ldots , m$
such that
![]() $\mathbf {x} \in \partial S$
. By the above observation, we need to have
$\mathbf {x} \in \partial S$
. By the above observation, we need to have
![]() $\mathbf {x} \in \mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k )$
. So
$\mathbf {x} \in \mathrm {conv}_{\partial S \cap U_m } (\partial S \cap Z_k )$
. So
![]() $\mathbf {x}$
belongs to the left-hand side of (6.8). Conversely, if
$\mathbf {x}$
belongs to the left-hand side of (6.8). Conversely, if
![]() $\mathbf {x}$
is in the left-hand side of (6.8), then
$\mathbf {x}$
is in the left-hand side of (6.8), then
![]() $\mathbf {x} \in \partial S$
for some
$\mathbf {x} \in \partial S$
for some
![]() $S \in \mathcal {L}_i$
,
$S \in \mathcal {L}_i$
,
![]() $i=1,\ldots , m$
. By (6.7),
$i=1,\ldots , m$
. By (6.7),
![]() $\mathbf {x} \in \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
, so
$\mathbf {x} \in \bigcap _{j=1}^{m} \bigcap _{S \in \mathcal {L}_j} S$
, so
![]() $\mathbf {x}$
must be on the boundary of that intersection. The proof of (6.8) is completed.
$\mathbf {x}$
must be on the boundary of that intersection. The proof of (6.8) is completed.
Remark 6.8. Notice, in the theorem above, that if for some
![]() $S\in \mathcal {L}_i$
we have
$S\in \mathcal {L}_i$
we have
![]() $\partial S \cap Z_k = \emptyset $
, then the boundary piece
$\partial S \cap Z_k = \emptyset $
, then the boundary piece
![]() $\mathrm {conv}_{\partial S \cap U_m}(\partial S \cap Z_k)$
contributed by it is also empty. This means that
$\mathrm {conv}_{\partial S \cap U_m}(\partial S \cap Z_k)$
contributed by it is also empty. This means that
![]() $\mathrm {conv}_{U_m}(Z_k)$
is in the interior of the domain S. Therefore, such an S can be safely ignored from the intersection (c) to obtain the same result. So, in view of Theorem 6.7, we may write
$\mathrm {conv}_{U_m}(Z_k)$
is in the interior of the domain S. Therefore, such an S can be safely ignored from the intersection (c) to obtain the same result. So, in view of Theorem 6.7, we may write
 $$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ \partial S \cap Z_k \neq \emptyset}} S. \end{align} $$
$$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ \partial S \cap Z_k \neq \emptyset}} S. \end{align} $$
That is, the families
![]() $\mathcal {L}_i$
are not minimal and contain more spherical domains than needed.
$\mathcal {L}_i$
are not minimal and contain more spherical domains than needed.
Remark 6.9. Note that if
![]() $\mathrm {conv}_{U_m}(Z_k)$
has nonempty interior, then it is necessarily connected, for
$\mathrm {conv}_{U_m}(Z_k)$
has nonempty interior, then it is necessarily connected, for
![]() $m \geq 2$
. In this case, the pieces of the boundary, as described in Theorem 6.7 (b), that matter are the ones that are exactly of co-dimension one. Indeed, if for some spherical domain
$m \geq 2$
. In this case, the pieces of the boundary, as described in Theorem 6.7 (b), that matter are the ones that are exactly of co-dimension one. Indeed, if for some spherical domain
![]() $S \in \mathcal {L}_i$
,
$S \in \mathcal {L}_i$
,
![]() $\partial S \cap Z_k = \{\mathbf {z}_j \}$
for some
$\partial S \cap Z_k = \{\mathbf {z}_j \}$
for some
![]() $j = 1, \ldots , k$
, then the boundary piece contributed by it is the singleton
$j = 1, \ldots , k$
, then the boundary piece contributed by it is the singleton
![]() $\{\mathbf {z}_j \}$
. Since this is a closed connected subset of
$\{\mathbf {z}_j \}$
. Since this is a closed connected subset of
![]() $\hat {\mathbb {R}}^n$
, the boundary point cannot be isolated. By Theorem 6.7, the boundary pieces are finitely many. So, there is a boundary piece that intersects every neighborhood of
$\hat {\mathbb {R}}^n$
, the boundary point cannot be isolated. By Theorem 6.7, the boundary pieces are finitely many. So, there is a boundary piece that intersects every neighborhood of
![]() $\mathbf {z}_j$
(since every point in
$\mathbf {z}_j$
(since every point in
![]() $\hat {\mathbb {R}}^n$
has a countable basis). Let
$\hat {\mathbb {R}}^n$
has a countable basis). Let
![]() $S' \in \mathcal {L}_{i'}$
be the spherical domain that generates this boundary piece. Then, because
$S' \in \mathcal {L}_{i'}$
be the spherical domain that generates this boundary piece. Then, because
![]() $\partial S'$
is closed, we must have
$\partial S'$
is closed, we must have
![]() $\mathbf {z}_j \in \partial S'$
, and thus,
$\mathbf {z}_j \in \partial S'$
, and thus,
![]() $\mathbf {z}_j$
is in the boundary piece generated by
$\mathbf {z}_j$
is in the boundary piece generated by
![]() $S'$
. Therefore, we may also ignore those spherical domains
$S'$
. Therefore, we may also ignore those spherical domains
![]() $S \in \mathcal {L}_i$
such that
$S \in \mathcal {L}_i$
such that
![]() $| \partial S \cap Z_k | < 2$
. That is,
$| \partial S \cap Z_k | < 2$
. That is,
 $$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} S. \end{align} $$
$$ \begin{align} \mathrm{conv}_{ U_m}(Z_k) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} S. \end{align} $$
We may not be able to ignore more spherical domains without additional hypotheses. If
![]() $|\partial S \cap Z_k| = 2$
, then the boundary piece generated by S may contribute nontrivially to the boundary of the
$|\partial S \cap Z_k| = 2$
, then the boundary piece generated by S may contribute nontrivially to the boundary of the
![]() $U_m$
-convex hull depending on the position and number of poles.
$U_m$
-convex hull depending on the position and number of poles.
Remark 6.10. If
![]() $\mathrm {conv}_{U_m}(Z_k)$
has empty interior, then it is contained in some sphere. We may consider that sphere to be our new ambient space. We can do this repeatedly until we have an ambient space, such that
$\mathrm {conv}_{U_m}(Z_k)$
has empty interior, then it is contained in some sphere. We may consider that sphere to be our new ambient space. We can do this repeatedly until we have an ambient space, such that
![]() $\mathrm {conv}_{U_m}(Z_k)$
has nonempty interior relative to it. In this ambient space, we can apply Theorem 6.7 to express it as an intersection of spherical domains.
$\mathrm {conv}_{U_m}(Z_k)$
has nonempty interior relative to it. In this ambient space, we can apply Theorem 6.7 to express it as an intersection of spherical domains.
Recall Definition 2.4 of the pole set associated to a subset Z of
![]() $\hat {\mathbb {R}}^n$
. Because of the above description of
$\hat {\mathbb {R}}^n$
. Because of the above description of
![]() $\mathrm {conv}_{U_m} (Z_k)$
as intersection of finite number of spherical domains, we obtain the following corollary.
$\mathrm {conv}_{U_m} (Z_k)$
as intersection of finite number of spherical domains, we obtain the following corollary.
Corollary 6.11 Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
![]() $\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
,
$\mathbf {u}_1 ,\ldots , \mathbf {u}_m \in \hat {\mathbb {R}}^n$
,
![]() ${m \geq 2}$
, be distinct (but not necessarily distinct from
${m \geq 2}$
, be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
), such that
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
), such that
![]() $\mathrm {conv}_{U_m} (Z_k)$
has nonempty interior. Then,
$\mathrm {conv}_{U_m} (Z_k)$
has nonempty interior. Then,
 $$ \begin{align} \mathrm{conv}_{Z_k} (U_m) \subseteq \mathcal{P} ( \mathrm{conv}_{U_m} (Z_k)) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align} $$
$$ \begin{align} \mathrm{conv}_{Z_k} (U_m) \subseteq \mathcal{P} ( \mathrm{conv}_{U_m} (Z_k)) = \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align} $$
Proof For any
![]() $S\in \mathcal {L}_i$
, with
$S\in \mathcal {L}_i$
, with
![]() $|\partial S \cap Z_k| \geq 2$
, we have
$|\partial S \cap Z_k| \geq 2$
, we have
![]() $U_m \subset \text {cl}(S^c)$
and
$U_m \subset \text {cl}(S^c)$
and
![]() $Z_k\cap S^c = \emptyset $
. So
$Z_k\cap S^c = \emptyset $
. So
![]() $\text {cl}(S^c)$
is convex with respect to all
$\text {cl}(S^c)$
is convex with respect to all
![]() $\mathbf {z}_j$
, and we get
$\mathbf {z}_j$
, and we get
 $$ \begin{align*}\mbox{conv}_{Z_k} (U_m) \subseteq \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align*} $$
$$ \begin{align*}\mbox{conv}_{Z_k} (U_m) \subseteq \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align*} $$
Next, suppose
![]() $\mathbf {v}$
does not belong to the right-hand side of (6.13). Then,
$\mathbf {v}$
does not belong to the right-hand side of (6.13). Then,
![]() $\mathbf {v} \in \mathrm {int} (S)$
for some
$\mathbf {v} \in \mathrm {int} (S)$
for some
![]() $S \in \mathcal {L}_i$
with
$S \in \mathcal {L}_i$
with
![]() $|\partial S \cap Z_k| \geq 2$
, say
$|\partial S \cap Z_k| \geq 2$
, say
![]() $\mathbf {z}_1 , \mathbf {z}_2 \in \partial S$
. Then,
$\mathbf {z}_1 , \mathbf {z}_2 \in \partial S$
. Then,
![]() $\mathrm {arc}_{\mathbf {v}} [\mathbf {z}_1 , \mathbf {z}_2] \not \subseteq S$
, so by (6.12),
$\mathrm {arc}_{\mathbf {v}} [\mathbf {z}_1 , \mathbf {z}_2] \not \subseteq S$
, so by (6.12),
![]() $\mathbf {v} \not \in \mathcal {P}(\mbox {conv}_{U_m}(Z_k))$
. Therefore,
$\mathbf {v} \not \in \mathcal {P}(\mbox {conv}_{U_m}(Z_k))$
. Therefore,
 $$ \begin{align*}\mathcal{P}(\mbox{conv}_{U_m}(Z_k)) \subseteq \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align*} $$
$$ \begin{align*}\mathcal{P}(\mbox{conv}_{U_m}(Z_k)) \subseteq \bigcap_{i=1}^m \bigcap_{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \mathrm{cl}(S^c). \end{align*} $$
Finally, for any
![]() $\mathbf {v}$
in the right-hand side of (6.13) and any
$\mathbf {v}$
in the right-hand side of (6.13) and any
![]() $S\in \mathcal {L}_i$
with
$S\in \mathcal {L}_i$
with
![]() $ |\partial S \cap Z_k| \geq 2$
, we have
$ |\partial S \cap Z_k| \geq 2$
, we have
![]() $\mathbf {v} \not \in \mbox {int}(S)$
and so S is
$\mathbf {v} \not \in \mbox {int}(S)$
and so S is
![]() $\mathbf {v}$
-convex. Therefore, the right-hand side of (6.12) is
$\mathbf {v}$
-convex. Therefore, the right-hand side of (6.12) is
![]() $\mathbf {v}$
-convex, and so we conclude that
$\mathbf {v}$
-convex, and so we conclude that
![]() $\mathbf {v} \in \mathcal {P}(\mbox {conv}_{U_m}(Z_k))$
. Thus,
$\mathbf {v} \in \mathcal {P}(\mbox {conv}_{U_m}(Z_k))$
. Thus,
 $$ \begin{align*}\bigcap _{i=1}^m \bigcap _{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \text{cl}(S^c) \subseteq \mathcal{P}(\mbox{conv}_{U_m}(Z_k)). \end{align*} $$
$$ \begin{align*}\bigcap _{i=1}^m \bigcap _{\substack{S \in \mathcal{L}_i \\ |\partial S \cap Z_k| \geq 2}} \text{cl}(S^c) \subseteq \mathcal{P}(\mbox{conv}_{U_m}(Z_k)). \end{align*} $$
This completes the proof.
The next example extends Example 4.1(f) from [Reference Sendov, Sendov and Wang11].
Example 6.12. Consider spherical domains
![]() $S_1 , \ldots , S_k \subset \hat {\mathbb {R}}^n$
, such that
$S_1 , \ldots , S_k \subset \hat {\mathbb {R}}^n$
, such that
![]() $S_i\cap S_j$
has nonempty interior and
$S_i\cap S_j$
has nonempty interior and
![]() $S_i \nsubseteq S_j$
for all
$S_i \nsubseteq S_j$
for all
![]() $i \neq j$
. For any
$i \neq j$
. For any
![]() $\mathbf {v} \in \{0,1 \}^k$
, define
$\mathbf {v} \in \{0,1 \}^k$
, define
Let
![]() $\mathbf {e} := [1, \ldots , 1] \in \{0,1 \}^k$
. Then,
$\mathbf {e} := [1, \ldots , 1] \in \{0,1 \}^k$
. Then,
![]() $A_{\mathbf {e} - \mathbf {v}} \subseteq \mathcal {P} (A_{\mathbf {v}})$
and
$A_{\mathbf {e} - \mathbf {v}} \subseteq \mathcal {P} (A_{\mathbf {v}})$
and
Example 3.8 shows that
![]() $\mathcal {P} (S_i) = \mathrm {cl}(S_i^c)$
, and vice versa. Therefore, it is clear that
$\mathcal {P} (S_i) = \mathrm {cl}(S_i^c)$
, and vice versa. Therefore, it is clear that
![]() $A_{\mathbf {e} - \mathbf {v}} \subseteq \mathcal {P} (A_{\mathbf {v}})$
. Figure 4 illustrates the case when equality holds. However, the equality does not hold in general, as Figure 5 shows.
$A_{\mathbf {e} - \mathbf {v}} \subseteq \mathcal {P} (A_{\mathbf {v}})$
. Figure 4 illustrates the case when equality holds. However, the equality does not hold in general, as Figure 5 shows.

Figure 4: Illustrating Example 6.12 when
![]() $A_{[0,0,1]} = \mathcal {P} (A_{[1,1,0]})$
.
$A_{[0,0,1]} = \mathcal {P} (A_{[1,1,0]})$
.

Figure 5: Illustrating Example 6.12 when
![]() $A_{[0,0,1,1]} \subsetneq \mathcal {P} (A_{[1,1,0,0]})$
.
$A_{[0,0,1,1]} \subsetneq \mathcal {P} (A_{[1,1,0,0]})$
.
Let the condition on the right-hand side of (6.14) hold and fix a point
![]() $\mathbf {u} \not \in A_{\mathbf {e} - \mathbf {v}}$
. Then, there is some i, such that
$\mathbf {u} \not \in A_{\mathbf {e} - \mathbf {v}}$
. Then, there is some i, such that
![]() $\mathbf {u} \not \in \mathrm {cl}(S_i^c)$
(the case when
$\mathbf {u} \not \in \mathrm {cl}(S_i^c)$
(the case when
![]() $\mathbf {u} \not \in S_i$
is anaologous), but
$\mathbf {u} \not \in S_i$
is anaologous), but
![]() $A_{\mathbf {v}} \subset S_i$
. Such an
$A_{\mathbf {v}} \subset S_i$
. Such an
![]() $S_i$
would not be convex with respect to
$S_i$
would not be convex with respect to
![]() $\mathbf {u}$
: if
$\mathbf {u}$
: if
![]() $\{\mathbf {x}_1 , \mathbf {x}_2 \} \subset \partial S_i \cap \partial A_{\mathbf {v}}$
, then
$\{\mathbf {x}_1 , \mathbf {x}_2 \} \subset \partial S_i \cap \partial A_{\mathbf {v}}$
, then
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {x}_1 , \mathbf {x}_2] \nsubseteq S_i$
. Since
$\mathrm {arc}_{\mathbf {u}} [\mathbf {x}_1 , \mathbf {x}_2] \nsubseteq S_i$
. Since
![]() $A_{\mathbf {v}} \subset S_i$
, this implies that
$A_{\mathbf {v}} \subset S_i$
, this implies that
![]() $A_{\mathbf {v}}$
cannot be convex with respect to
$A_{\mathbf {v}}$
cannot be convex with respect to
![]() $\mathbf {u}$
. Therefore,
$\mathbf {u}$
. Therefore,
![]() $A_{\mathbf {e} - \mathbf {v}} \supseteq \mathcal {P}(A_{\mathbf {v}})$
, establishing (6.14).
$A_{\mathbf {e} - \mathbf {v}} \supseteq \mathcal {P}(A_{\mathbf {v}})$
, establishing (6.14).
Theorem 6.13 For any
![]() $Z \subseteq \hat {\mathbb {R}}^n$
, we have
$Z \subseteq \hat {\mathbb {R}}^n$
, we have
![]() $Z \subseteq \mathcal {P}(\mathcal {P}(Z)).$
$Z \subseteq \mathcal {P}(\mathcal {P}(Z)).$
Proof Note that if Z is either
![]() $\hat {\mathbb {R}}^n$
,
$\hat {\mathbb {R}}^n$
,
![]() $\emptyset $
, or a singleton, then
$\emptyset $
, or a singleton, then
![]() $\mathcal {P}(Z) = \hat {\mathbb {R}}^n$
, and so
$\mathcal {P}(Z) = \hat {\mathbb {R}}^n$
, and so
![]() $\mathcal {P}(\mathcal {P}(Z)) = \hat {\mathbb {R}}^n$
. Similarly, if
$\mathcal {P}(\mathcal {P}(Z)) = \hat {\mathbb {R}}^n$
. Similarly, if
![]() $\mathcal {P}(Z)$
is a singleton, then
$\mathcal {P}(Z)$
is a singleton, then
![]() $\mathcal {P}(\mathcal {P}(Z)) = \hat {\mathbb {R}}^n$
.
$\mathcal {P}(\mathcal {P}(Z)) = \hat {\mathbb {R}}^n$
.
Thus, we may assume that both Z and
![]() $\mathcal {P}(Z)$
contain at least two points. We need to show that if
$\mathcal {P}(Z)$
contain at least two points. We need to show that if
![]() $\mathbf {z}_1 \in Z$
and if
$\mathbf {z}_1 \in Z$
and if
![]() $\mathbf {u}_1, \mathbf {u}_2 \in \mathcal {P}(Z)$
, then
$\mathbf {u}_1, \mathbf {u}_2 \in \mathcal {P}(Z)$
, then
![]() $\mathrm {arc}_{\mathbf {z}_1}[ \mathbf {u}_1 , \mathbf {u}_2 ] \subseteq \mathcal {P}(Z)$
. Assume that the points
$\mathrm {arc}_{\mathbf {z}_1}[ \mathbf {u}_1 , \mathbf {u}_2 ] \subseteq \mathcal {P}(Z)$
. Assume that the points
![]() $\mathbf {z}_1, \mathbf {u}_1$
, and
$\mathbf {z}_1, \mathbf {u}_1$
, and
![]() $\mathbf {u}_2$
are distinct; otherwise, the inclusion
$\mathbf {u}_2$
are distinct; otherwise, the inclusion
![]() $\mathrm {arc}_{\mathbf {z}_1}[ \mathbf {u}_1 , \mathbf {u}_2 ] \subseteq \mathcal {P}(Z)$
is trivial. In other words, one has to show that any
$\mathrm {arc}_{\mathbf {z}_1}[ \mathbf {u}_1 , \mathbf {u}_2 ] \subseteq \mathcal {P}(Z)$
is trivial. In other words, one has to show that any
![]() $\mathbf {v} \in \mathrm {arc}_{\mathbf {z}_1}[\mathbf {u}_1, \mathbf {u}_2]$
is a pole for Z; that is, for any
$\mathbf {v} \in \mathrm {arc}_{\mathbf {z}_1}[\mathbf {u}_1, \mathbf {u}_2]$
is a pole for Z; that is, for any
![]() $\mathbf {z}_2, \mathbf {z}_3 \in Z$
, we have
$\mathbf {z}_2, \mathbf {z}_3 \in Z$
, we have
![]() $\mathrm {arc}_{\mathbf {v}}[\mathbf {z}_2,\mathbf {z}_3] \subseteq Z$
. If
$\mathrm {arc}_{\mathbf {v}}[\mathbf {z}_2,\mathbf {z}_3] \subseteq Z$
. If
![]() $\mathbf {z}_2, \mathbf {z}_3$
happen to be on the circle determined by
$\mathbf {z}_2, \mathbf {z}_3$
happen to be on the circle determined by
![]() $\mathbf {z}_1, \mathbf {u}_1, \mathbf {u}_2$
, and
$\mathbf {z}_1, \mathbf {u}_1, \mathbf {u}_2$
, and
![]() $\mathbf {v}$
, then it is easy to see that
$\mathbf {v}$
, then it is easy to see that
![]() $\mathrm {arc}_{\mathbf {v}}[\mathbf {z}_2,\mathbf {z}_3] \subseteq Z$
by considering several cases (we omit the details). Otherwise, by Remark 6.10, we may restrict to a smaller dimensional ambient space that has dimension at least two and where the set
$\mathrm {arc}_{\mathbf {v}}[\mathbf {z}_2,\mathbf {z}_3] \subseteq Z$
by considering several cases (we omit the details). Otherwise, by Remark 6.10, we may restrict to a smaller dimensional ambient space that has dimension at least two and where the set
![]() $\mbox {conv}_{\{\mathbf {u}_1, \mathbf {u}_2\}}\{ \mathbf {z}_1, \mathbf {z}_2, \mathbf {z}_3\}$
has nonempty interior. By Corollary 6.11, we have
$\mbox {conv}_{\{\mathbf {u}_1, \mathbf {u}_2\}}\{ \mathbf {z}_1, \mathbf {z}_2, \mathbf {z}_3\}$
has nonempty interior. By Corollary 6.11, we have
This shows the first inclusion in
while the second inclusion follows since
![]() $\mathbf {u}_1, \mathbf {u}_2 \in \mathcal {P}(Z)$
. Finally, since
$\mathbf {u}_1, \mathbf {u}_2 \in \mathcal {P}(Z)$
. Finally, since
![]() $\mathbf {z}_2, \mathbf {z}_3 \in Z$
were arbitrary, we get that
$\mathbf {z}_2, \mathbf {z}_3 \in Z$
were arbitrary, we get that
![]() $\mathbf {v} \in \mathcal {P}(Z)$
.
$\mathbf {v} \in \mathcal {P}(Z)$
.
Remark 6.14. As a consequence of the above theorem, given any set
![]() $Z \subseteq \hat {\mathbb {R}}^n$
, we get two increasing chains of sets
$Z \subseteq \hat {\mathbb {R}}^n$
, we get two increasing chains of sets
and
Let
Then, we get that
![]() $\mathcal {P}(A) \supseteq B$
and
$\mathcal {P}(A) \supseteq B$
and
![]() $\mathcal {P} (B) \supseteq A$
. Indeed, for any
$\mathcal {P} (B) \supseteq A$
. Indeed, for any
![]() $\mathbf {z}_1, \mathbf {z}_2 \in A$
and
$\mathbf {z}_1, \mathbf {z}_2 \in A$
and
![]() $\mathbf {u} \in B$
, there is an integer k, such that
$\mathbf {u} \in B$
, there is an integer k, such that
![]() $\mathbf {z}_1, \mathbf {z}_2 \in \mathcal {P}^{2k}(Z)$
and
$\mathbf {z}_1, \mathbf {z}_2 \in \mathcal {P}^{2k}(Z)$
and
![]() $\mathbf {u} \in \mathcal {P}^{2k+1}(Z)$
. This shows that
$\mathbf {u} \in \mathcal {P}^{2k+1}(Z)$
. This shows that
![]() $\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \mathbf {z}_2] \subseteq \mathcal {P}^{2k}(Z) \subseteq A.$
$\mathrm {arc}_{\mathbf {u}} [\mathbf {z}_1, \mathbf {z}_2] \subseteq \mathcal {P}^{2k}(Z) \subseteq A.$
Open Problem Characterize the pairs of sets
![]() $(A,B)$
in
$(A,B)$
in
![]() $\hat {\mathbb {R}}^n$
, such that
$\hat {\mathbb {R}}^n$
, such that
![]() $\mathcal {P}(A) \supseteq B$
and
$\mathcal {P}(A) \supseteq B$
and
![]() $\mathcal {P} (B) \supseteq A$
. Moreover, characterize the pairs of sets
$\mathcal {P} (B) \supseteq A$
. Moreover, characterize the pairs of sets
![]() $(A,B)$
in
$(A,B)$
in
![]() $\hat {\mathbb {R}}^n$
, with the stronger conditions that
$\hat {\mathbb {R}}^n$
, with the stronger conditions that
![]() $\mathcal {P}(A) = B$
and
$\mathcal {P}(A) = B$
and
![]() $\mathcal {P} (B) = A$
.
$\mathcal {P} (B) = A$
.
To conclude, we express Corollary 6.4 algebraically in the special case
Doing so gives us the following identities.
Corollary 6.15 Given distinct points
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {R}^{n-1}$
, and
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {R}^{n-1}$
, and
![]() $t, \alpha _j,\beta _j \in [ 0, 1]$
, for
$t, \alpha _j,\beta _j \in [ 0, 1]$
, for
![]() $1\leq j \leq k$
, such that
$1\leq j \leq k$
, such that
 $$ \begin{align*}\sum _{j=1}^k \alpha_j = \sum _{j=1}^k \beta_j = 1, \end{align*} $$
$$ \begin{align*}\sum _{j=1}^k \alpha_j = \sum _{j=1}^k \beta_j = 1, \end{align*} $$
there exist
![]() $ \gamma _i, \delta _{i,j} \in [0,1]$
, for
$ \gamma _i, \delta _{i,j} \in [0,1]$
, for
![]() $1\leq i \leq n$
and
$1\leq i \leq n$
and
![]() $1\leq j \leq k$
, such that
$1\leq j \leq k$
, such that
 $$ \begin{align*}\sum _{i=1}^n \gamma_i =\sum _{j=1}^k \delta_{i,j} = 1 \mbox{ for all } 1\leq i \leq n \end{align*} $$
$$ \begin{align*}\sum _{i=1}^n \gamma_i =\sum _{j=1}^k \delta_{i,j} = 1 \mbox{ for all } 1\leq i \leq n \end{align*} $$
and satisfying
 $$ \begin{align*} \Big( t\Big( \sum _{i=1}^k \alpha_i (\mathbf{z}_i - \mathbf{u})\Big)^* + (1-t)\Big( \sum _{i=1}^k \beta_i (\mathbf{z}_i - \mathbf{u})\Big)^*\Big)^* = \sum _{i=1}^n \gamma_i \Big( \sum _{j=1}^k \delta_{i,j}(\mathbf{z}_j - \mathbf{u})^* \Big)^*. \end{align*} $$
$$ \begin{align*} \Big( t\Big( \sum _{i=1}^k \alpha_i (\mathbf{z}_i - \mathbf{u})\Big)^* + (1-t)\Big( \sum _{i=1}^k \beta_i (\mathbf{z}_i - \mathbf{u})\Big)^*\Big)^* = \sum _{i=1}^n \gamma_i \Big( \sum _{j=1}^k \delta_{i,j}(\mathbf{z}_j - \mathbf{u})^* \Big)^*. \end{align*} $$
Proof Clearly, the points
![]() $\sum _{i=1}^k \alpha _i \mathbf {z}_i,\sum _{i=1}^k \beta _i \mathbf {z}_i$
are in
$\sum _{i=1}^k \alpha _i \mathbf {z}_i,\sum _{i=1}^k \beta _i \mathbf {z}_i$
are in
![]() $\mbox {conv}\{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. For any
$\mbox {conv}\{\mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. For any
![]() $t \in [0,1]$
, we have
$t \in [0,1]$
, we have
 $$ \begin{align*} \mathbf{u} + \Big( t (\sum _{i=1}^k \alpha_i \mathbf{z}_i - \mathbf{u})^* + (1-t) (\sum _{i=1}^k \beta_i \mathbf{z}_i - \mathbf{u})^* \Big)^* &\in \mathrm{conv}_{\mathbf{u}}(\mathrm{conv} \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k \}) \\ &= \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k \}). \end{align*} $$
$$ \begin{align*} \mathbf{u} + \Big( t (\sum _{i=1}^k \alpha_i \mathbf{z}_i - \mathbf{u})^* + (1-t) (\sum _{i=1}^k \beta_i \mathbf{z}_i - \mathbf{u})^* \Big)^* &\in \mathrm{conv}_{\mathbf{u}}(\mathrm{conv} \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k \}) \\ &= \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k \}). \end{align*} $$
By Carathéodory’s theorem, there are points
![]() $\mathbf {x}_1, \ldots , \mathbf {x}_n \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
and parameters
$\mathbf {x}_1, \ldots , \mathbf {x}_n \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
and parameters
![]() $\gamma _1, \ldots , \gamma _n \in [0,1]$
, such that
$\gamma _1, \ldots , \gamma _n \in [0,1]$
, such that
![]() $\sum _{i=1}^n \gamma _i = 1$
and
$\sum _{i=1}^n \gamma _i = 1$
and
 $$ \begin{align} \mathbf{u} + \Big( t (\sum _{i=1}^k \alpha_i \mathbf{z}_i - \mathbf{u})^* + (1-t) (\sum _{i=1}^k \beta_i \mathbf{z}_i - \mathbf{u})^* \Big)^* = \sum _{i=1}^n \gamma_i \mathbf{x}_i. \end{align} $$
$$ \begin{align} \mathbf{u} + \Big( t (\sum _{i=1}^k \alpha_i \mathbf{z}_i - \mathbf{u})^* + (1-t) (\sum _{i=1}^k \beta_i \mathbf{z}_i - \mathbf{u})^* \Big)^* = \sum _{i=1}^n \gamma_i \mathbf{x}_i. \end{align} $$
Since
![]() $\mathbf {x}_i \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
, there must be parameters
$\mathbf {x}_i \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 ,\ldots , \mathbf {z}_k \}$
, there must be parameters
![]() $\delta _{i,1}, \ldots , \delta _{i,k}$
such that
$\delta _{i,1}, \ldots , \delta _{i,k}$
such that
![]() $\sum _{j=1}^k \delta _{i,j} =1$
and
$\sum _{j=1}^k \delta _{i,j} =1$
and
 $$ \begin{align} \mathbf{x}_i = \mathbf{u} + \Big( \sum _{j=1}^k \delta_{i,j} (\mathbf{z}_j - \mathbf{u})^* \Big)^*, \mbox{ for all } i=1,\ldots, k. \end{align} $$
$$ \begin{align} \mathbf{x}_i = \mathbf{u} + \Big( \sum _{j=1}^k \delta_{i,j} (\mathbf{z}_j - \mathbf{u})^* \Big)^*, \mbox{ for all } i=1,\ldots, k. \end{align} $$
Substituting the equations (6.17) back into (6.16) and simplifying gives the stated identity.
In particular, when
![]() $n=3$
, we get an algebraic relationship in the complex plane.
$n=3$
, we get an algebraic relationship in the complex plane.
Corollary 6.16 Given distinct points
![]() $\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {C}$
, and
$\mathbf {u}, \mathbf {z}_1, \ldots , \mathbf {z}_k \in \mathbb {C}$
, and
![]() $t, \alpha _j,\beta _j \in [ 0, 1]$
, for
$t, \alpha _j,\beta _j \in [ 0, 1]$
, for
![]() $1\leq j \leq k$
, such that
$1\leq j \leq k$
, such that
 $$ \begin{align*}\sum _{j=1}^k \alpha_j = \sum _{j=1}^k \beta_j = 1, \end{align*} $$
$$ \begin{align*}\sum _{j=1}^k \alpha_j = \sum _{j=1}^k \beta_j = 1, \end{align*} $$
there exist
![]() $ \gamma _i, \delta _{i,j} \in [0,1]$
, for
$ \gamma _i, \delta _{i,j} \in [0,1]$
, for
![]() $1\leq i \leq 3$
and
$1\leq i \leq 3$
and
![]() $1\leq j \leq k$
, such that
$1\leq j \leq k$
, such that
 $$ \begin{align*}\sum _{i=1}^3 \gamma_i =\sum _{j=1}^k \delta_{i,j} = 1 \mbox{ for all } 1\leq i \leq 3 \end{align*} $$
$$ \begin{align*}\sum _{i=1}^3 \gamma_i =\sum _{j=1}^k \delta_{i,j} = 1 \mbox{ for all } 1\leq i \leq 3 \end{align*} $$
and satisfying
 $$ \begin{align*}\frac{1}{ \frac{t}{\sum _{i=1}^k \alpha_i (\mathbf{z}_i - \mathbf{u})} + \frac{1-t}{\sum _{i=1}^k \beta_i (\mathbf{z}_i - \mathbf{u})}} = \frac{\gamma_1}{ \sum _{j=1}^k \frac{\delta_{1,j}}{\mathbf{z}_j - \mathbf{u}}} + \frac{ \gamma_2}{ \sum _{j=1}^k \frac{\delta_{2,j}}{\mathbf{z}_j - \mathbf{u}}} + \frac{\gamma_3}{ \sum _{j=1}^k \frac{\delta_{3,j}}{\mathbf{z}_j - \mathbf{u}}}. \end{align*} $$
$$ \begin{align*}\frac{1}{ \frac{t}{\sum _{i=1}^k \alpha_i (\mathbf{z}_i - \mathbf{u})} + \frac{1-t}{\sum _{i=1}^k \beta_i (\mathbf{z}_i - \mathbf{u})}} = \frac{\gamma_1}{ \sum _{j=1}^k \frac{\delta_{1,j}}{\mathbf{z}_j - \mathbf{u}}} + \frac{ \gamma_2}{ \sum _{j=1}^k \frac{\delta_{2,j}}{\mathbf{z}_j - \mathbf{u}}} + \frac{\gamma_3}{ \sum _{j=1}^k \frac{\delta_{3,j}}{\mathbf{z}_j - \mathbf{u}}}. \end{align*} $$
7 Conclusions
In conclusion, the paper aims to establish the foundations of a theory of polar convexity in the case of finite-dimensional Euclidean spaces to build on. Polar convexity, as a generalization of classical convexity, enjoys many unique properties – the Duality Theorem, for example – that could not be formulated in the classical setting. These properties, however, are still applicable to the classical setting, and we hope that these will be exploited to approach many classical problems.
The theory is still in its infancy. One could ask what are the polar convex functions and if they have applications to optimization problems that parallel those of classical convex functions. Section 6 looks at convexification of sets with respect to multiple poles. These sets are convex, in the classical sense, if one of the poles is
![]() $\infty $
. Thus, if a set is convex with respect to multiple poles, it is natural to ask what additional properties do these super convex sets have. Also in Section 6, we give a description of the convex hull of finitely many points with respect to finitely many poles. It is natural to ask for similar descriptions when one or both of these sets are infinite. Concrete answers to such questions are not known even in the case of nicely behaved infinite sets and may be a topic of further research.
$\infty $
. Thus, if a set is convex with respect to multiple poles, it is natural to ask what additional properties do these super convex sets have. Also in Section 6, we give a description of the convex hull of finitely many points with respect to finitely many poles. It is natural to ask for similar descriptions when one or both of these sets are infinite. Concrete answers to such questions are not known even in the case of nicely behaved infinite sets and may be a topic of further research.
Appendix
This section contains deferred proofs and results that may distract the reader from the main development.
Proof of Lemma 2.1
By definition, we have
 $$ \begin{align} \mathbf{u} + \big( t (\mathbf{z}_1 - &\mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^* \big)^* \nonumber \\ &= \mathbf{u} + \frac{t (\mathbf{z}_1 - \mathbf{u})^* + (1-t)(\mathbf{z}_2 - \mathbf{u})^* }{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \nonumber \\ & =\mathbf{u} \Big( 1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}\Big) \\ &\hspace{0.5cm} + \frac{t\mathbf{z}_1 / \|\mathbf{z}_1 - \mathbf{u} \|^2 + (1-t)\mathbf{z}_2 / \|\mathbf{z}_2 - \mathbf{u} \|^2}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}. \nonumber \end{align} $$
$$ \begin{align} \mathbf{u} + \big( t (\mathbf{z}_1 - &\mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^* \big)^* \nonumber \\ &= \mathbf{u} + \frac{t (\mathbf{z}_1 - \mathbf{u})^* + (1-t)(\mathbf{z}_2 - \mathbf{u})^* }{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \nonumber \\ & =\mathbf{u} \Big( 1 - \frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}\Big) \\ &\hspace{0.5cm} + \frac{t\mathbf{z}_1 / \|\mathbf{z}_1 - \mathbf{u} \|^2 + (1-t)\mathbf{z}_2 / \|\mathbf{z}_2 - \mathbf{u} \|^2}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}. \nonumber \end{align} $$
We look at the two terms of the last displayed expression separately. For the first term, we have
 $$ \begin{align*} \mathbf{u} \Big( 1 - &\frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}\Big)\\ & = \mathbf{u} \frac{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 - t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} - (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \\ & = \frac{\mathbf{u}}{D} \big( \| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2} \|\mathbf{z}_2 - \mathbf{u}\|^{2} \\ & \hspace{6cm}- t \|\mathbf{z}_2 - \mathbf{u}\|^{2} - (1-t) \|\mathbf{z}_1 - \mathbf{u}\|^{2} \big), \end{align*} $$
$$ \begin{align*} \mathbf{u} \Big( 1 - &\frac{t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} + (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2}\Big)\\ & = \mathbf{u} \frac{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 - t / \|\mathbf{z}_1 - \mathbf{u}\|^{2} - (1-t) / \|\mathbf{z}_2 - \mathbf{u}\|^{2}}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} \\ & = \frac{\mathbf{u}}{D} \big( \| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2} \|\mathbf{z}_2 - \mathbf{u}\|^{2} \\ & \hspace{6cm}- t \|\mathbf{z}_2 - \mathbf{u}\|^{2} - (1-t) \|\mathbf{z}_1 - \mathbf{u}\|^{2} \big), \end{align*} $$
where
In the numerator, expand
![]() $\| t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^*\|^2$
as a dot product and multiply throughout by
$\| t (\mathbf {z}_1 - \mathbf {u})^* + (1-t) (\mathbf {z}_2 - \mathbf {u})^*\|^2$
as a dot product and multiply throughout by
![]() $ \|\mathbf {z}_1 - \mathbf {u}\|^{2} \|\mathbf {z}_2 - \mathbf {u}\|^{2}$
. After elementary simplifications, we arrive at
$ \|\mathbf {z}_1 - \mathbf {u}\|^{2} \|\mathbf {z}_2 - \mathbf {u}\|^{2}$
. After elementary simplifications, we arrive at
 $$ \begin{align*} \frac{\mathbf{u}}{D} & \big( -t(1-t)\|\mathbf{z}_2 - \mathbf{u}\|^2 - t(1-t) \|\mathbf{z}_1 - \mathbf{u}\|^2 + t(1-t) \langle \mathbf{z}_1 - \mathbf{u}, \mathbf{z}_2 - \mathbf{u} \rangle \\ & \hspace{7cm}+ t(1-t) \langle \mathbf{z}_2 - \mathbf{u}, \mathbf{z}_1 - \mathbf{u} \rangle \big) \\ & = \frac{\mathbf{u}}{D}\big( -t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 \big) \\ & = \mathbf{u} \frac{-t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2}\|\mathbf{z}_2 - \mathbf{u}\|^{2}} {\| t (\mathbf{z}_1 - \mathbf{u})\|\mathbf{z}_2 - \mathbf{u}\|^{2} + (1-t) (\mathbf{z}_2 - \mathbf{u})\|\mathbf{z}_1 - \mathbf{u}\|^{2}\|^2} \\ & = \mathbf{u} \frac{O(\|\mathbf{u} \|^4)}{\|\mathbf{u} \|^6}. \end{align*} $$
$$ \begin{align*} \frac{\mathbf{u}}{D} & \big( -t(1-t)\|\mathbf{z}_2 - \mathbf{u}\|^2 - t(1-t) \|\mathbf{z}_1 - \mathbf{u}\|^2 + t(1-t) \langle \mathbf{z}_1 - \mathbf{u}, \mathbf{z}_2 - \mathbf{u} \rangle \\ & \hspace{7cm}+ t(1-t) \langle \mathbf{z}_2 - \mathbf{u}, \mathbf{z}_1 - \mathbf{u} \rangle \big) \\ & = \frac{\mathbf{u}}{D}\big( -t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 \big) \\ & = \mathbf{u} \frac{-t(1-t)\|\mathbf{z}_1 - \mathbf{z}_2 \|^2 \|\mathbf{z}_1 - \mathbf{u}\|^{2}\|\mathbf{z}_2 - \mathbf{u}\|^{2}} {\| t (\mathbf{z}_1 - \mathbf{u})\|\mathbf{z}_2 - \mathbf{u}\|^{2} + (1-t) (\mathbf{z}_2 - \mathbf{u})\|\mathbf{z}_1 - \mathbf{u}\|^{2}\|^2} \\ & = \mathbf{u} \frac{O(\|\mathbf{u} \|^4)}{\|\mathbf{u} \|^6}. \end{align*} $$
Now we look at the second term in (7.1) and multiply its numerator and denominator by
![]() $\|\mathbf {u}\|^2$
. Then, it can be developed as
$\|\mathbf {u}\|^2$
. Then, it can be developed as
 $$ \begin{align*} \frac{t\mathbf{z}_1 / \|\mathbf{z}_1 - \mathbf{u} \|^2 + (1-t)\mathbf{z}_2 / \|\mathbf{z}_2 - \mathbf{u} \|^2}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} &=\frac{{t \mathbf{z}_1}{\Big\| \frac{\mathbf{z}_1}{\|\mathbf{u} \|} - \frac{\mathbf{u}}{\| \mathbf{u} \|} \Big\|^{-2}} + {(1-t) \mathbf{z}_2}{\Big\| \frac{\mathbf{z}_2}{\|\mathbf{u} \|} - \frac{\mathbf{u}}{\| \mathbf{u} \|} \Big\|^{-2}}}{\| t \big(\frac{\mathbf{z}_1}{\|\mathbf{u}\|} - \frac{\mathbf{u}}{\| \mathbf{u}\|}\big)^* + (1-t) \big(\frac{\mathbf{z}_2}{\|\mathbf{u}\|} - \frac{\mathbf{u}}{\| \mathbf{u}\|}\big)^*\|^2}. \end{align*} $$
$$ \begin{align*} \frac{t\mathbf{z}_1 / \|\mathbf{z}_1 - \mathbf{u} \|^2 + (1-t)\mathbf{z}_2 / \|\mathbf{z}_2 - \mathbf{u} \|^2}{\| t (\mathbf{z}_1 - \mathbf{u})^* + (1-t) (\mathbf{z}_2 - \mathbf{u})^*\|^2} &=\frac{{t \mathbf{z}_1}{\Big\| \frac{\mathbf{z}_1}{\|\mathbf{u} \|} - \frac{\mathbf{u}}{\| \mathbf{u} \|} \Big\|^{-2}} + {(1-t) \mathbf{z}_2}{\Big\| \frac{\mathbf{z}_2}{\|\mathbf{u} \|} - \frac{\mathbf{u}}{\| \mathbf{u} \|} \Big\|^{-2}}}{\| t \big(\frac{\mathbf{z}_1}{\|\mathbf{u}\|} - \frac{\mathbf{u}}{\| \mathbf{u}\|}\big)^* + (1-t) \big(\frac{\mathbf{z}_2}{\|\mathbf{u}\|} - \frac{\mathbf{u}}{\| \mathbf{u}\|}\big)^*\|^2}. \end{align*} $$
Thus, taking the limit as
![]() $\|\mathbf {u}\| \rightarrow \infty $
, the first term in (7.1) converges to
$\|\mathbf {u}\| \rightarrow \infty $
, the first term in (7.1) converges to
![]() $0$
, while the second converges to
$0$
, while the second converges to
![]() $ t\mathbf {z}_1 + (1-t)\mathbf {z}_2$
. This completes the proof of the lemma.
$ t\mathbf {z}_1 + (1-t)\mathbf {z}_2$
. This completes the proof of the lemma.
Lemma 7.1 Let the points
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
$\mathbf {z}_1, \ldots , \mathbf {z}_k \in \hat {\mathbb {R}}^n$
be distinct and let
![]() $\mathbf {u}_1, \mathbf {u}_2\in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
$\mathbf {u}_1, \mathbf {u}_2\in \hat {\mathbb {R}}^n$
be distinct (but not necessarily distinct from
![]() $\mathbf {z}_1, \ldots , \mathbf {z}_k$
). Suppose that not all of
$\mathbf {z}_1, \ldots , \mathbf {z}_k$
). Suppose that not all of
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}_1 , \mathbf {u}_2\}$
lie on a
![]() $(n - 1)\mbox {-sphere}$
. Then,
$(n - 1)\mbox {-sphere}$
. Then,
where the families
![]() $\mathcal {S}_i$
and
$\mathcal {S}_i$
and
![]() $\mathcal {L}_i$
are defined in (6.1) and (6.2).
$\mathcal {L}_i$
are defined in (6.1) and (6.2).
Proof By symmetry, we may assume that
![]() $i=1$
. Since
$i=1$
. Since
![]() $\mathcal {L}_1 \subseteq \mathcal {S}_1$
, it is clear that
$\mathcal {L}_1 \subseteq \mathcal {S}_1$
, it is clear that
To see the other containment, without loss of generality, assume
![]() $\mathbf {u}_1 = \infty $
. The set
$\mathbf {u}_1 = \infty $
. The set
![]() $\mathcal {L}_1$
consists of all supporting half-spaces that either correspond to the maximal faces of the polytope
$\mathcal {L}_1$
consists of all supporting half-spaces that either correspond to the maximal faces of the polytope
![]() $\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
separating
$\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
separating
![]() $\mathbf {u}_2$
and
$\mathbf {u}_2$
and
![]() $\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
or those that correspond to the maximal faces of the cone
$\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
or those that correspond to the maximal faces of the cone
or both. Since
![]() $\mathcal {S}_1$
is the set of all half-spaces that separate
$\mathcal {S}_1$
is the set of all half-spaces that separate
![]() $\mathbf {u}_2$
and
$\mathbf {u}_2$
and
![]() $\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, we have that
$\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, we have that
![]() $\bigcap _{D \in \mathcal {L}_1} D \subseteq S$
for all
$\bigcap _{D \in \mathcal {L}_1} D \subseteq S$
for all
![]() $S \in \mathcal {S}_1$
.
$S \in \mathcal {S}_1$
.
Proof of Theorem 6.3
Without loss of generality, we may assume
![]() $\mathbf {u}_2 = \infty $
and write
$\mathbf {u}_2 = \infty $
and write
![]() $\mathbf {u}_1$
as
$\mathbf {u}_1$
as
![]() $\mathbf {u}$
. In the proof, we need both families (6.1) and (6.2). So
$\mathbf {u}$
. In the proof, we need both families (6.1) and (6.2). So
![]() $\mathcal {S}_1$
,
$\mathcal {S}_1$
,
![]() $\mathcal {L}_1$
correspond to
$\mathcal {L}_1$
correspond to
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\mathcal {S}_2$
,
$\mathcal {S}_2$
,
![]() $\mathcal {L}_2$
correspond to
$\mathcal {L}_2$
correspond to
![]() $\infty $
. It is clear that
$\infty $
. It is clear that
 $$ \begin{align*}\mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \}) \subseteq \bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S \end{align*} $$
$$ \begin{align*}\mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \}) \subseteq \bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S \end{align*} $$
because the right-hand side is convex with respect to both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
and contains
$\infty $
and contains
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. We aim to show the opposite inclusion.
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. We aim to show the opposite inclusion.
 $$ \begin{align*}\bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S \subseteq \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \}). \end{align*} $$
$$ \begin{align*}\bigcap_{i=1}^2 \bigcap_{S \in \mathcal{S}_i} S \subseteq \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \}). \end{align*} $$
If
![]() $\infty \in \mathrm {int}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
, then
$\infty \in \mathrm {int}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
, then
![]() $\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) = \hat {\mathbb {R}}^n$
, so the inclusion is trivial. Thus, we assume that
$\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) = \hat {\mathbb {R}}^n$
, so the inclusion is trivial. Thus, we assume that
![]() $\infty \not \in \mathrm {int}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
and consider four cases based on whether
$\infty \not \in \mathrm {int}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
and consider four cases based on whether
![]() $\infty $
and
$\infty $
and
![]() $\mathbf {u}$
are in
$\mathbf {u}$
are in
![]() $\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
or not.
$\{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
or not.
Case 1: Assume that
![]() $\infty , \mathbf {u} \not \in \{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. We consider two sub-cases.
$\infty , \mathbf {u} \not \in \{\mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
. We consider two sub-cases.
Case 1.a: If
![]() $\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, by Lemma 5.1, part (1), there is a spherical domain S, containing
$\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, by Lemma 5.1, part (1), there is a spherical domain S, containing
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and having
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and having
![]() $\mathbf {u}$
on its boundary, that strongly separates
$\mathbf {u}$
on its boundary, that strongly separates
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
![]() $\{\infty \}$
. Since
$\{\infty \}$
. Since
![]() $\infty $
is in
$\infty $
is in
![]() $\mathrm {cl}(S^c)$
, S is convex with respect to both
$\mathrm {cl}(S^c)$
, S is convex with respect to both
![]() $\infty $
and
$\infty $
and
![]() $\mathbf {u}$
, we get that
$\mathbf {u}$
, we get that
![]() $S \in \mathcal {S}_1$
. So
$S \in \mathcal {S}_1$
. So
![]() $\infty \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
$\infty \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
Since
![]() $\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, then
$\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, then
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
is closed and bounded. Thus, the set
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
is closed and bounded. Thus, the set
![]() $\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is closed and therefore also closed in
$\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is closed and therefore also closed in
![]() $\hat {\mathbb {R}}^n \smallsetminus \{ \infty \}$
. So, by Lemma 5.1, part (1), for any
$\hat {\mathbb {R}}^n \smallsetminus \{ \infty \}$
. So, by Lemma 5.1, part (1), for any
![]() $\mathbf {x} \not \in \mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) \cup \{ \infty \}$
, there is a spherical domain S, containing
$\mathbf {x} \not \in \mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}) \cup \{ \infty \}$
, there is a spherical domain S, containing
![]() $\mathrm {conv} (\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
and having
$\mathrm {conv} (\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
and having
![]() $\infty $
on its boundary, that strongly separates the sets
$\infty $
on its boundary, that strongly separates the sets
![]() $\{\mathbf {x}\}$
and
$\{\mathbf {x}\}$
and
![]() $\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
. We want to show that
$\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
. We want to show that
![]() $\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
$\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
Indeed, if
![]() $\mathbf {u} \in \mathrm {cl}(S^c)$
, then since S is convex with respect to both
$\mathbf {u} \in \mathrm {cl}(S^c)$
, then since S is convex with respect to both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
, we have
$\infty $
, we have
![]() $S \in \mathcal {S}_2$
. So,
$S \in \mathcal {S}_2$
. So,
![]() $\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. If
$\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. If
![]() $\mathbf {u} \not \in \mathrm {cl}(S^c)$
, then
$\mathbf {u} \not \in \mathrm {cl}(S^c)$
, then
![]() $\mathrm {cl}(S^c)$
is a closed
$\mathrm {cl}(S^c)$
is a closed
![]() $\mathbf {u}$
-convex spherical domain containing both
$\mathbf {u}$
-convex spherical domain containing both
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $\infty $
and not containing
$\infty $
and not containing
![]() $\mathbf {u}$
(in particular,
$\mathbf {u}$
(in particular,
![]() $\mathbf {u}$
is not on the boundary of
$\mathbf {u}$
is not on the boundary of
![]() $\mathrm {cl}(S^c)$
). Next,
$\mathrm {cl}(S^c)$
). Next,
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \} $
is a
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \} $
is a
![]() $\mathbf {u}$
-convex set that is closed in
$\mathbf {u}$
-convex set that is closed in
![]() $\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
. By Lemma 5.1, part (1), there is a spherical domain
$\hat {\mathbb {R}}^n \smallsetminus \{\mathbf {u}\}$
. By Lemma 5.1, part (1), there is a spherical domain
![]() $S'$
, having
$S'$
, having
![]() $\mathbf {u}$
on its boundary, containing
$\mathbf {u}$
on its boundary, containing
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \} $
and strongly separating
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \} $
and strongly separating
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
![]() $\mathrm {cl} (S^c)$
. Since
$\mathrm {cl} (S^c)$
. Since
![]() $\infty \in \mathrm {cl} (S^c)$
, we have that
$\infty \in \mathrm {cl} (S^c)$
, we have that
![]() $S'$
does not contain
$S'$
does not contain
![]() $\infty $
and has
$\infty $
and has
![]() $\mathbf {u}$
on its boundary. So,
$\mathbf {u}$
on its boundary. So,
![]() $S' \in \mathcal {S}_1$
, and since
$S' \in \mathcal {S}_1$
, and since
![]() $\mathbf {x} \in \mathrm {cl} (S^c)$
, we get that
$\mathbf {x} \in \mathrm {cl} (S^c)$
, we get that
![]() $\mathbf {x} \not \in S'$
and conclude that
$\mathbf {x} \not \in S'$
and conclude that
![]() $\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. This concludes the proof in the case when
$\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. This concludes the proof in the case when
![]() $\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
$\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
.
Case 1.b: Suppose now
![]() $\infty \in \partial \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Then, by Corollary 4.5, this is equivalent to
$\infty \in \partial \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Then, by Corollary 4.5, this is equivalent to
![]() $\mathbf {u} \in \partial \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Every domain
$\mathbf {u} \in \partial \mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. Every domain
![]() $S \in \mathcal {S}_1$
is
$S \in \mathcal {S}_1$
is
![]() $\mathbf {u}$
-convex and contains
$\mathbf {u}$
-convex and contains
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
by definition, so it contains
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
by definition, so it contains
![]() $\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. This implies that S also contains
$\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. This implies that S also contains
![]() $\infty $
, but by definition,
$\infty $
, but by definition,
![]() $\infty \in \mathrm {cl}(S^c)$
, and therefore,
$\infty \in \mathrm {cl}(S^c)$
, and therefore,
![]() $\infty \in \partial S$
. Similarly,
$\infty \in \partial S$
. Similarly,
![]() $\mathbf {u} \in \partial S$
for all
$\mathbf {u} \in \partial S$
for all
![]() $S \in \mathcal {S}_2$
, so we conclude that
$S \in \mathcal {S}_2$
, so we conclude that
![]() $\mathcal {S}_1$
and
$\mathcal {S}_1$
and
![]() $\mathcal {S}_2$
contain the same domains. Since a domain
$\mathcal {S}_2$
contain the same domains. Since a domain
![]() $S \in \mathcal {L}_1$
or
$S \in \mathcal {L}_1$
or
![]() $S \in \mathcal {L}_2$
is forced to have both
$S \in \mathcal {L}_2$
is forced to have both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
on its boundary, they are all half-spaces. Therefore, for all
$\infty $
on its boundary, they are all half-spaces. Therefore, for all
![]() $S \in \mathcal {L}_1 \cup \mathcal {L}_2$
, we get that
$S \in \mathcal {L}_1 \cup \mathcal {L}_2$
, we get that
 $$ \begin{align} \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} &= \mathrm{aff}_{\infty} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} \\ &= \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \}. \nonumber \end{align} $$
$$ \begin{align} \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} &= \mathrm{aff}_{\infty} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} \\ &= \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \}. \nonumber \end{align} $$
To see the last equality, note that we have
The first equality in (7.3) shows that the families
![]() $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
![]() $\mathcal {L}_2$
are equal. By assumption,
$\mathcal {L}_2$
are equal. By assumption,
![]() $\mathbf {z}_1 , \ldots , \mathbf {z}_k ,\mathbf {u}, \infty $
are not all on a hyperplane. So, using Lemma 7.1, we have
$\mathbf {z}_1 , \ldots , \mathbf {z}_k ,\mathbf {u}, \infty $
are not all on a hyperplane. So, using Lemma 7.1, we have
 $$ \begin{align*}\bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap _{S \in \mathcal{L}_1} S. \end{align*} $$
$$ \begin{align*}\bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap _{S \in \mathcal{L}_1} S. \end{align*} $$
Let
![]() $\mathcal {L}$
be the family of spherical domains described in Lemma 6.1. Then, the second equality in (7.3) shows that
$\mathcal {L}$
be the family of spherical domains described in Lemma 6.1. Then, the second equality in (7.3) shows that
![]() $\mathcal {L}_1 \subseteq \mathcal {L}$
. Note that if
$\mathcal {L}_1 \subseteq \mathcal {L}$
. Note that if
![]() $S \in \mathcal {L}$
and
$S \in \mathcal {L}$
and
![]() $\infty \in \partial S$
, then
$\infty \in \partial S$
, then
![]() $S \in \mathcal {L}_1$
. Therefore, if
$S \in \mathcal {L}_1$
. Therefore, if
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
, then
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
, then
![]() $\infty \not \in \partial S$
; in other words,
$\infty \not \in \partial S$
; in other words,
![]() $\partial S$
is a bounded set. Any spherical domain
$\partial S$
is a bounded set. Any spherical domain
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
contains
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
contains
![]() $\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and has
$\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and has
![]() $\mathbf {u}$
on its boundary, and hence S contains
$\mathbf {u}$
on its boundary, and hence S contains
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Thus, S is unbounded since
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Thus, S is unbounded since
![]() $\infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, by Corollary 4.4. Since
$\infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, by Corollary 4.4. Since
![]() $\mathcal {L} \smallsetminus \mathcal {L}_1$
is a finite set, there is an
$\mathcal {L} \smallsetminus \mathcal {L}_1$
is a finite set, there is an
![]() $R> 0$
such that
$R> 0$
such that
![]() $D(\mathbf {0}; R)^c \subset S \smallsetminus \{\mathbf {u}\}$
for all
$D(\mathbf {0}; R)^c \subset S \smallsetminus \{\mathbf {u}\}$
for all
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. (Here,
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. (Here,
![]() $D(\mathbf {0}; R)$
is the open ball with center
$D(\mathbf {0}; R)$
is the open ball with center
![]() $\mathbf {0}$
and radius R.) Thus, we have
$\mathbf {0}$
and radius R.) Thus, we have
Therefore,
 $$ \begin{align*} \bigcap_{S \in \mathcal{L}_1} S \cap D(\mathbf{0}; R)^c &\subseteq \Big( \bigcap_{S \in \mathcal{L}_1} S\Big) \cap \Big( \bigcap_{S \in \mathcal{L} \smallsetminus \mathcal{L}_1} S \smallsetminus \{ \mathbf{u} \}\Big) \\ & = \bigcap_{S \in \mathcal{L}} S \smallsetminus \{ \mathbf{u} \} = \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}, \end{align*} $$
$$ \begin{align*} \bigcap_{S \in \mathcal{L}_1} S \cap D(\mathbf{0}; R)^c &\subseteq \Big( \bigcap_{S \in \mathcal{L}_1} S\Big) \cap \Big( \bigcap_{S \in \mathcal{L} \smallsetminus \mathcal{L}_1} S \smallsetminus \{ \mathbf{u} \}\Big) \\ & = \bigcap_{S \in \mathcal{L}} S \smallsetminus \{ \mathbf{u} \} = \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}, \end{align*} $$
where in the last equality, we used Lemma 6.1. Since we are in a case where
![]() $\mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and
$\mathbf {u} \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and
![]() $\mathbf {u} \in \partial \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, the boundary of the intersection of half-spaces,
$\mathbf {u} \in \partial \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
, the boundary of the intersection of half-spaces,
![]() $\bigcap _{S \in \mathcal {L}_1} S$
, contains at least a line, so
$\bigcap _{S \in \mathcal {L}_1} S$
, contains at least a line, so
and by Lemma 7.1, we have
 $$ \begin{align*}\bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap_{S \in \mathcal{L}_1} S \subseteq \mathrm{conv}( \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}). \end{align*} $$
$$ \begin{align*}\bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap_{S \in \mathcal{L}_1} S \subseteq \mathrm{conv}( \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}). \end{align*} $$
Case 2: Assume that
![]() $\infty \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, but
$\infty \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
, but
![]() $\mathbf {u} \not \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. By definition,
$\mathbf {u} \not \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. By definition,
If
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, then
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, then
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1,\ldots , k \}$
. So we have
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1,\ldots , k \}$
. So we have
![]() $ \infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
, and
$ \infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
, and
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \} = \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. This, of course, implies that
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \} = \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. This, of course, implies that
Therefore, any spherical domain S, convex with respect to both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
, that contains
$\infty $
, that contains
![]() $\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
is forced to contain
$\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
is forced to contain
![]() $\infty $
because it contains
$\infty $
because it contains
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
. Thus,
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
. Thus,
![]() $\infty \in \partial S$
because S is convex. This implies that the families
$\infty \in \partial S$
because S is convex. This implies that the families
![]() $\mathcal {S}_1, \mathcal {S}_2, \mathcal {L}_1$
, and
$\mathcal {S}_1, \mathcal {S}_2, \mathcal {L}_1$
, and
![]() $\mathcal {L}_2$
corresponding to the sets
$\mathcal {L}_2$
corresponding to the sets
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
![]() $\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
are the same. So, we can consider the set
$\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
are the same. So, we can consider the set
![]() $\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\} \smallsetminus \{\infty \}$
and argue as in Case 1.
$\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\} \smallsetminus \{\infty \}$
and argue as in Case 1.
Therefore, we may assume that
![]() $\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. If
$\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. If
![]() $S \in \mathcal {L}_1$
, then by definition,
$S \in \mathcal {L}_1$
, then by definition,
![]() $\infty \in \mathrm {cl}(S^c)$
, but the premise of the current case implies that
$\infty \in \mathrm {cl}(S^c)$
, but the premise of the current case implies that
![]() $\infty \in S$
, so we need to have
$\infty \in S$
, so we need to have
![]() $\infty \in \partial S$
. Since in addition,
$\infty \in \partial S$
. Since in addition,
![]() $\mathbf {u} \in \partial S$
, one can see that
$\mathbf {u} \in \partial S$
, one can see that
 $$ \begin{align} \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} &= \mathrm{aff}_{\infty} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} \\ &= \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \}. \nonumber \end{align} $$
$$ \begin{align} \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} &= \mathrm{aff}_{\infty} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} , \infty \} \cap \partial S \} \\ &= \mathrm{aff}_{\mathbf{u}} \{ \{ \mathbf{z}_1 ,\ldots , \mathbf{z}_k, \mathbf{u} \} \cap \partial S \}. \nonumber \end{align} $$
The first equality shows that
![]() $\mathcal {L}_1 \subseteq \mathcal {L}_2$
. Therefore, we have
$\mathcal {L}_1 \subseteq \mathcal {L}_2$
. Therefore, we have
 $$ \begin{align} \bigcap_{i=1}^2 \bigcap _{S\in \mathcal{L}_i} S = \bigcap _{S\in \mathcal{L}_2} S. \end{align} $$
$$ \begin{align} \bigcap_{i=1}^2 \bigcap _{S\in \mathcal{L}_i} S = \bigcap _{S\in \mathcal{L}_2} S. \end{align} $$
The family
![]() $\mathcal {L}_1$
is the set of all half-spaces that support the maximal faces of the cone
$\mathcal {L}_1$
is the set of all half-spaces that support the maximal faces of the cone
![]() $\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
. (Note that the latter cone has a nonempty interior, or else
$\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
. (Note that the latter cone has a nonempty interior, or else
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}, \infty \}$
lie on a
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}, \infty \}$
lie on a
![]() $(n - 1)\mbox {-sphere}$
, contradicting our assumption.) That is,
$(n - 1)\mbox {-sphere}$
, contradicting our assumption.) That is,
 $$ \begin{align} \bigcap _{S\in \mathcal{L}_1} S &= \mathbf{u} + \mathrm{cone}\{ \mathbf{z}_1 - \mathbf{u} , \ldots , \mathbf{z}_k - \mathbf{u}\} \nonumber \\ &= \{ \mathbf{u} + t(\mathbf{z}-\mathbf{u}) : t \ge 0, \mathbf{z} \in \mathrm{conv}(\{ \mathbf{z}_1, \ldots , \mathbf{z}_k\} \smallsetminus \{ \infty \}) \} \cup \{\infty\}. \end{align} $$
$$ \begin{align} \bigcap _{S\in \mathcal{L}_1} S &= \mathbf{u} + \mathrm{cone}\{ \mathbf{z}_1 - \mathbf{u} , \ldots , \mathbf{z}_k - \mathbf{u}\} \nonumber \\ &= \{ \mathbf{u} + t(\mathbf{z}-\mathbf{u}) : t \ge 0, \mathbf{z} \in \mathrm{conv}(\{ \mathbf{z}_1, \ldots , \mathbf{z}_k\} \smallsetminus \{ \infty \}) \} \cup \{\infty\}. \end{align} $$
A domain
![]() $S \in \mathcal {L}_2$
can be of two types: either
$S \in \mathcal {L}_2$
can be of two types: either
![]() $\mathbf {u} \in \partial S$
or
$\mathbf {u} \in \partial S$
or
![]() $\mathbf {u} \in S^c$
. In the first case, S is a half-space that supports a maximal face of the cone
$\mathbf {u} \in S^c$
. In the first case, S is a half-space that supports a maximal face of the cone
![]() $\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
, while in the second case, S is a half-space that supports a maximal face of the polytope
$\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
, while in the second case, S is a half-space that supports a maximal face of the polytope
![]() $\mathrm {conv}(\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \smallsetminus \{ \infty \})$
that separates
$\mathrm {conv}(\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\} \smallsetminus \{ \infty \})$
that separates
![]() $\mathbf {u}$
from
$\mathbf {u}$
from
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. Thus,
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. Thus,
We need to prove that
Let again
![]() $\mathcal {L}$
be the family as described in Lemma 6.1. Then, the second equality in (7.4) shows that
$\mathcal {L}$
be the family as described in Lemma 6.1. Then, the second equality in (7.4) shows that
![]() $\mathcal {L}_1 \subseteq \mathcal {L}$
. Note that if
$\mathcal {L}_1 \subseteq \mathcal {L}$
. Note that if
![]() $S \in \mathcal {L}$
and
$S \in \mathcal {L}$
and
![]() $\infty \in \partial S$
, then
$\infty \in \partial S$
, then
![]() $S \in \mathcal {L}_1$
. Therefore, if
$S \in \mathcal {L}_1$
. Therefore, if
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
, then
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
, then
![]() $\infty \not \in \partial S$
; in other words,
$\infty \not \in \partial S$
; in other words,
![]() $\partial S$
is a bounded set. Any spherical domain
$\partial S$
is a bounded set. Any spherical domain
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
contains
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
contains
![]() $\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and has
$\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
and has
![]() $\mathbf {u}$
on its boundary; hence, S contains
$\mathbf {u}$
on its boundary; hence, S contains
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Thus, S is unbounded since
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Thus, S is unbounded since
![]() $\infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
by Corollary 4.4. Since
$\infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
by Corollary 4.4. Since
![]() $\mathcal {L} \smallsetminus \mathcal {L}_1$
is a finite set, there is an
$\mathcal {L} \smallsetminus \mathcal {L}_1$
is a finite set, there is an
![]() $R> 0$
such that
$R> 0$
such that
![]() $D(\mathbf {0}; R)^c \subset S \smallsetminus \{\mathbf {u}\}$
for all
$D(\mathbf {0}; R)^c \subset S \smallsetminus \{\mathbf {u}\}$
for all
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. We get that
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. We get that
Therefore,
 $$ \begin{align} \big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}\cup D(\mathbf{0}; R)^c \big) \cap\bigcap _{S\in \mathcal{L}_1} S &\subseteq \Big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\} \cup \bigcap _{S\in \mathcal{L}} S \Big) \smallsetminus \{ \mathbf{u} \} \\ &= \bigcap _{S\in \mathcal{L}} S \smallsetminus \{ \mathbf{u} \} = \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}, \nonumber \end{align} $$
$$ \begin{align} \big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}\cup D(\mathbf{0}; R)^c \big) \cap\bigcap _{S\in \mathcal{L}_1} S &\subseteq \Big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\} \cup \bigcap _{S\in \mathcal{L}} S \Big) \smallsetminus \{ \mathbf{u} \} \\ &= \bigcap _{S\in \mathcal{L}} S \smallsetminus \{ \mathbf{u} \} = \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}, \nonumber \end{align} $$
where in the last equality, we used Lemma 6.1. Using representations (7.6) and (7.7), one can see that for large enough R, we have
Thus, taking the convex hull from both sides in (7.8), we obtain
 $$ \begin{align*} \mathrm{conv}( \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}) &\supseteq \mathrm{conv}\Big( \big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}\cup D(\mathbf{0}; R)^c \big) \cap\bigcap _{S\in \mathcal{L}_1} S \Big) \\ &= \mathrm{conv}\Big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \} \cup \Big( D(\mathbf{0}; R)^c \cap \bigcap _{S\in \mathcal{L}_1} S\Big) \Big) \\ &= \mathrm{conv} \Big( \{\mathbf{z}_1, \ldots , \mathbf{z}_k \} \cup \Big(D(\mathbf{0}; R)^c \cap \bigcap _{S\in \mathcal{L}_2} S \Big) \Big) \\ &= \bigcap _{S\in \mathcal{L}_2} S. \end{align*} $$
$$ \begin{align*} \mathrm{conv}( \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}) &\supseteq \mathrm{conv}\Big( \big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}\cup D(\mathbf{0}; R)^c \big) \cap\bigcap _{S\in \mathcal{L}_1} S \Big) \\ &= \mathrm{conv}\Big( \{ \mathbf{z}_1, \ldots , \mathbf{z}_k \} \cup \Big( D(\mathbf{0}; R)^c \cap \bigcap _{S\in \mathcal{L}_1} S\Big) \Big) \\ &= \mathrm{conv} \Big( \{\mathbf{z}_1, \ldots , \mathbf{z}_k \} \cup \Big(D(\mathbf{0}; R)^c \cap \bigcap _{S\in \mathcal{L}_2} S \Big) \Big) \\ &= \bigcap _{S\in \mathcal{L}_2} S. \end{align*} $$
This concludes the proof in this case.
Case 3: Assume
![]() $\mathbf {u} \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
but
$\mathbf {u} \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\}$
but
![]() $\infty \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. By definition,
$\infty \not \in \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. By definition,
If
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
, then we have
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
, then we have
![]() $ \infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \} $
and
$ \infty \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \} $
and
![]() $\mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \} = \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Therefore, as before, any spherical domain S convex with respect to both
$\mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \} = \mathrm {conv} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
. Therefore, as before, any spherical domain S convex with respect to both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
that contains
$\infty $
that contains
![]() $\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
is forced to contain
$\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
is forced to contain
![]() $\mathbf {u}$
because it contains
$\mathbf {u}$
because it contains
![]() $\mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
. Thus,
$\mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
. Thus,
![]() $\mathbf {u} \in \partial S$
because S is
$\mathbf {u} \in \partial S$
because S is
![]() $\mathbf {u}$
-convex. This implies that the families
$\mathbf {u}$
-convex. This implies that the families
![]() $\mathcal {S}_1 , \mathcal {S}_2, \mathcal {L}_1$
, and
$\mathcal {S}_1 , \mathcal {S}_2, \mathcal {L}_1$
, and
![]() $\mathcal {L}_2$
corresponding to the sets
$\mathcal {L}_2$
corresponding to the sets
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
and
![]() $\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
are the same. So we can consider the set
$\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1 , \ldots , k \}$
are the same. So we can consider the set
![]() $\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\} \smallsetminus \{\mathbf {u} \}$
and argue as in Case 1.
$\{ \mathbf {z}_1 , \ldots , \mathbf {z}_k\} \smallsetminus \{\mathbf {u} \}$
and argue as in Case 1.
Assume now
![]() $\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
; that is,
$\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
; that is,
![]() $\mathbf {u}$
is an extreme point of
$\mathbf {u}$
is an extreme point of
![]() $\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. By Corollary 4.6, this also implies that
$\mathrm {conv}\{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. By Corollary 4.6, this also implies that
![]() $\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, so
$\infty \not \in \mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
, so
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is closed and bounded. Therefore,
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
is closed and bounded. Therefore,
![]() $\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is closed and bounded. We aim to show that
$\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \})$
is closed and bounded. We aim to show that
 $$ \begin{align*}\mbox{If } \mathbf{x} \not\in \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}), \mbox{ then } \mathbf{x} \not\in \bigcap _{i=1}^2 \bigcap _{S\in \mathcal{S}_i} S. \end{align*} $$
$$ \begin{align*}\mbox{If } \mathbf{x} \not\in \mathrm{conv}(\mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1, \ldots , \mathbf{z}_k\}), \mbox{ then } \mathbf{x} \not\in \bigcap _{i=1}^2 \bigcap _{S\in \mathcal{S}_i} S. \end{align*} $$
If
![]() $\mathbf {x} = \infty $
, then since
$\mathbf {x} = \infty $
, then since
![]() $\infty \not \in \mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
, by Lemma 5.1, part (1), there is a spherical domain S, containing
$\infty \not \in \mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
, by Lemma 5.1, part (1), there is a spherical domain S, containing
![]() $\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and having
$\mathrm {conv}_{\mathbf {u}}\{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and having
![]() $\mathbf {u}$
on its boundary, that strongly separates
$\mathbf {u}$
on its boundary, that strongly separates
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and
![]() $\{\infty \}$
. Since
$\{\infty \}$
. Since
![]() $\infty $
is in
$\infty $
is in
![]() $S^c$
, S is convex with respect to both
$S^c$
, S is convex with respect to both
![]() $\infty $
and
$\infty $
and
![]() $\mathbf {u}$
, we get that
$\mathbf {u}$
, we get that
![]() $S \in \mathcal {S}_1$
. So
$S \in \mathcal {S}_1$
. So
![]() $\infty \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
$\infty \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
.
If
![]() $\mathbf {x} \not \in \mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}) \cup \{ \infty \}$
, then there is a closed half-space S strongly separating
$\mathbf {x} \not \in \mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}) \cup \{ \infty \}$
, then there is a closed half-space S strongly separating
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\})$
and containing the latter set. If
$\mathrm {conv}(\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\})$
and containing the latter set. If
![]() $\mathbf {u} \in \mathrm {cl}(S^c)$
, then S is also
$\mathbf {u} \in \mathrm {cl}(S^c)$
, then S is also
![]() $\mathbf {u}$
-convex, so
$\mathbf {u}$
-convex, so
![]() $S \in \mathcal {S}_2$
and
$S \in \mathcal {S}_2$
and
![]() $\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. If
$\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. If
![]() $\mathbf {u} \in \mathrm {int}(S)$
, then
$\mathbf {u} \in \mathrm {int}(S)$
, then
![]() $\mathrm {cl}(S^c)$
is a
$\mathrm {cl}(S^c)$
is a
![]() $\mathbf {u}$
-convex domain disjoint from
$\mathbf {u}$
-convex domain disjoint from
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and containing both
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
and containing both
![]() $\infty $
and
$\infty $
and
![]() $\mathbf {x}$
. By Lemma 5.1, part (1), there is a spherical domain
$\mathbf {x}$
. By Lemma 5.1, part (1), there is a spherical domain
![]() $S'$
, having
$S'$
, having
![]() $\mathbf {u}$
on its boundary, containing
$\mathbf {u}$
on its boundary, containing
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \} $
and strongly separating
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \} $
and strongly separating
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u} , i=1,\ldots , k \}$
and
![]() $\mathrm {cl} (S^c)$
. Also, because
$\mathrm {cl} (S^c)$
. Also, because
![]() $\mathbf {u} \in \partial S'$
, we get that
$\mathbf {u} \in \partial S'$
, we get that
![]() $S'$
contains
$S'$
contains
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. Since
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1, \ldots , \mathbf {z}_k\}$
. Since
![]() $\infty \in \mathrm {cl} (S^c)$
, we have that
$\infty \in \mathrm {cl} (S^c)$
, we have that
![]() $S'$
does not contain
$S'$
does not contain
![]() $\infty $
and has
$\infty $
and has
![]() $\mathbf {u}$
on its boundary. So,
$\mathbf {u}$
on its boundary. So,
![]() $S' \in \mathcal {S}_1$
. Finally, since
$S' \in \mathcal {S}_1$
. Finally, since
![]() $\mathbf {x} \in \mathrm {cl} (S^c)$
, we get that
$\mathbf {x} \in \mathrm {cl} (S^c)$
, we get that
![]() $\mathbf {x} \not \in S'$
and conclude that
$\mathbf {x} \not \in S'$
and conclude that
![]() $\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. This concludes the proof in this case.
$\mathbf {x} \not \in \bigcap _{i=1}^2 \bigcap _{S \in \mathcal {S}_i} S$
. This concludes the proof in this case.
Case 4: Assume that
![]() $\infty , \mathbf {u} \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. If
$\infty , \mathbf {u} \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
. If
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1,\ldots , k \}$
, then
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1,\ldots , k \}$
, then
![]() $\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, \infty , i=1,\ldots , k \}$
. Then, by Theorem 4.3,
$\mathbf {u} \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, \infty , i=1,\ldots , k \}$
. Then, by Theorem 4.3,
Therefore, any spherical domain S, convex with respect to both
![]() $\mathbf {u}$
and
$\mathbf {u}$
and
![]() $\infty $
, that contains
$\infty $
, that contains
![]() $\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
is forced to contain
$\{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
is forced to contain
![]() $\infty $
because it contains
$\infty $
because it contains
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
. Thus,
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_i : \mathbf {z}_i \neq \infty , i=1 , \ldots , k \}$
. Thus,
![]() $\infty \in \partial S$
, because S is
$\infty \in \partial S$
, because S is
![]() $\infty $
-convex. This implies that the families
$\infty $
-convex. This implies that the families
![]() $\mathcal {S}_1,\mathcal {S}_2, \mathcal {L}_1$
, and
$\mathcal {S}_1,\mathcal {S}_2, \mathcal {L}_1$
, and
![]() $\mathcal {L}_2$
corresponding to the sets
$\mathcal {L}_2$
corresponding to the sets
![]() $\{ \mathbf {z}_1, \ldots , {\mathbf {z}}_k \}$
and
$\{ \mathbf {z}_1, \ldots , {\mathbf {z}}_k \}$
and
![]() $\{ {\mathbf {z}}_i : {\mathbf {z}}_i \neq \infty , i=1 , \ldots , k \}$
are the same. So, we can consider the set
$\{ {\mathbf {z}}_i : {\mathbf {z}}_i \neq \infty , i=1 , \ldots , k \}$
are the same. So, we can consider the set
![]() $\{ {\mathbf {z}}_1 , \ldots , {\mathbf {z}}_k\} \smallsetminus \{\infty \}$
and argue as in Case 3.
$\{ {\mathbf {z}}_1 , \ldots , {\mathbf {z}}_k\} \smallsetminus \{\infty \}$
and argue as in Case 3.
Assume that
![]() $\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1,\ldots , k \}$
. Then,
$\mathbf {u} \not \in \mathrm {conv} \{ \mathbf {z}_i : \mathbf {z}_i \neq \mathbf {u}, i=1,\ldots , k \}$
. Then,
Then, using Theorem 4.3, we obtain
It follows from definitions (6.1) and (6.2) that
![]() $\mathcal {S}_1 = \mathcal {S}_2$
and
$\mathcal {S}_1 = \mathcal {S}_2$
and
![]() $\mathcal {L}_1 = \mathcal {L}_2$
because all the domains
$\mathcal {L}_1 = \mathcal {L}_2$
because all the domains
![]() $S \in \mathcal {S}_1 \cup \mathcal {S}_2$
are forced to contain both
$S \in \mathcal {S}_1 \cup \mathcal {S}_2$
are forced to contain both
![]() $\infty $
and
$\infty $
and
![]() $\mathbf {u}$
on their boundary. Thus, the family
$\mathbf {u}$
on their boundary. Thus, the family
![]() $\mathcal {L}_1$
consists of all supporting half-spaces corresponding to the maximal faces of the cone
$\mathcal {L}_1$
consists of all supporting half-spaces corresponding to the maximal faces of the cone
![]() $\mathbf {u} + \mathrm {cone} \{ \mathbf {z}_1 - \mathbf {u}, \ldots , \mathbf {z}_k - \mathbf {u} \}$
. (Note that the latter cone has a nonempty interior, or else
$\mathbf {u} + \mathrm {cone} \{ \mathbf {z}_1 - \mathbf {u}, \ldots , \mathbf {z}_k - \mathbf {u} \}$
. (Note that the latter cone has a nonempty interior, or else
![]() $\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}, \infty \}$
lie on a
$\{ \mathbf {z}_1, \ldots , \mathbf {z}_k , \mathbf {u}, \infty \}$
lie on a
![]() $(n - 1)\mbox {-sphere}$
, contradicting our assumption.) So, using (7.2), one sees that
$(n - 1)\mbox {-sphere}$
, contradicting our assumption.) So, using (7.2), one sees that
 $$ \begin{align} \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap _{S \in \mathcal{L}_1} S = \mathbf{u} + \mathrm{cone}\{ \mathbf{z}_1 - \mathbf{u} , \ldots , \mathbf{z}_k - \mathbf{u}\}. \end{align} $$
$$ \begin{align} \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{S}_i} S = \bigcap _{i=1}^2 \bigcap _{S \in \mathcal{L}_i} S = \bigcap _{S \in \mathcal{L}_1} S = \mathbf{u} + \mathrm{cone}\{ \mathbf{z}_1 - \mathbf{u} , \ldots , \mathbf{z}_k - \mathbf{u}\}. \end{align} $$
To conclude the argument, it is sufficient to show
As before, let
![]() $\mathcal {L}$
be the family of spherical domains described in Lemma 6.1. Since
$\mathcal {L}$
be the family of spherical domains described in Lemma 6.1. Since
![]() $\infty \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, all the domains S in
$\infty \in \{ \mathbf {z}_1, \ldots , \mathbf {z}_k \}$
, all the domains S in
![]() $\mathcal {L}$
are unbounded. Note that
$\mathcal {L}$
are unbounded. Note that
![]() $\mathcal {L}_1 \subseteq \mathcal {L}$
. There are two types of domains in
$\mathcal {L}_1 \subseteq \mathcal {L}$
. There are two types of domains in
![]() $\mathcal {L}$
: those with
$\mathcal {L}$
: those with
![]() $\infty $
in their interior and those that have
$\infty $
in their interior and those that have
![]() $\infty $
on their boundary. The latter ones are those in
$\infty $
on their boundary. The latter ones are those in
![]() $\mathcal {L}_1$
. There are finitely many domains in
$\mathcal {L}_1$
. There are finitely many domains in
![]() $\mathcal {L}$
, and since the domains
$\mathcal {L}$
, and since the domains
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
have bounded boundaries, the boundaries are all in a ball
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
have bounded boundaries, the boundaries are all in a ball
![]() $D(\mathbf {0}; R)$
with large enough radius
$D(\mathbf {0}; R)$
with large enough radius
![]() $R>0$
. So, we can conclude that
$R>0$
. So, we can conclude that
![]() $D(\mathbf {0}; R)^c \cup \{ \mathbf {u} \}\subseteq S$
for all
$D(\mathbf {0}; R)^c \cup \{ \mathbf {u} \}\subseteq S$
for all
![]() $S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. Thus, by Lemma 6.1, we have
$S \in \mathcal {L} \smallsetminus \mathcal {L}_1$
. Thus, by Lemma 6.1, we have
 $$ \begin{align*} \bigcap_{S \in \mathcal{L}_1} S \cap \big( D(\mathbf{0}; R)^c \cup \{ \mathbf{u} \} \big)&\subseteq \Big( \bigcap_{S \in \mathcal{L}_1} S\Big) \cap \Big( \bigcap_{S \in \mathcal{L} \smallsetminus \mathcal{L}_1} S \Big) = \bigcap_{S \in \mathcal{L}} S \\ &= \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}. \end{align*} $$
$$ \begin{align*} \bigcap_{S \in \mathcal{L}_1} S \cap \big( D(\mathbf{0}; R)^c \cup \{ \mathbf{u} \} \big)&\subseteq \Big( \bigcap_{S \in \mathcal{L}_1} S\Big) \cap \Big( \bigcap_{S \in \mathcal{L} \smallsetminus \mathcal{L}_1} S \Big) = \bigcap_{S \in \mathcal{L}} S \\ &= \mathrm{conv}_{\mathbf{u}} \{ \mathbf{z}_1 , \ldots , \mathbf{z}_k \}. \end{align*} $$
Therefore, using (7.10), the set
![]() $\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
contains
$\mathrm {conv}_{\mathbf {u}} \{ \mathbf {z}_1 , \ldots , \mathbf {z}_k \}$
contains
![]() $\mathbf {u}$
and all points of
$\mathbf {u}$
and all points of
![]() $\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
beyond a certain radius. So, we conclude
$\mathbf {u} + \mathrm {cone}\{ \mathbf {z}_1 - \mathbf {u} , \ldots , \mathbf {z}_k - \mathbf {u}\}$
beyond a certain radius. So, we conclude
This completes the proof.