Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T22:47:58.386Z Has data issue: false hasContentIssue false
  • English
  • Français

On Nonstandard Hulls of Convex Spaces

Published online by Cambridge University Press:  20 November 2018

Steven F. Bellenot
Steven F. Bellenot*
Affiliation:
Florida State University, Tallahassee, Florida 32306
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A nonstandard hull of a TVS (locally convex topological vector space) 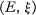is a standard TVS 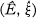constructed from a nonstandard model for 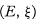[3]. If the nonstandard hulls of a TVS are independent of the non-standard model, we say that the TVS has invariant nonstandard hulls. This is (for complete spaces) the property that every finite element is inflnitesimally close to a standard point. We build on the work of Henson and Moore [4], to show that invariance of nonstandard hulls is a self dual property equivalent to bounded sets being precompact, for F and DF spaces, (see Theorem 4.4).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 141 - 147
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Bellenot, S. F., Prevarieties and interwinded completeness of locally convex spaces, Math. Ann. 217 (1975), 59–67,Google Scholar
2. Berenzanskii, LA., Inductively reflexive locally convex spaces, Soviet Math. Doklady (Translations from Russian) 9(2) (1968), 1080–1082.Google Scholar
3. Henson, C. W. and M∞re, L. C., Jr., The theory of nonstandard topological vector spaces, Trans. Amer. Math. Soc. 172 (1972), 193–206.Google Scholar
4. Invariance of the nonstandard hulls of locally convex spaces, Duke Math. J. 4-0 (1973), 193–206.Google Scholar
5. Hogbe-Nlend, H., Topologies et homologies nucléaires associées applications, Ann. Inst. Fourier (Grenoble) 23 (1973), fasc. 4, 89–104.Google Scholar
6. Horvath, J., Topological vector spaces and distributions (Addison-Wesley, Reading, Mass., vol. I 1966).Google Scholar
7. Kôthe, G., Topological vector spaces, I (Springer-Verlag, New York, 1969).Google Scholar
8. Peitsch, A., Nuclear locally convex spaces (Springer-Verlag, New York, 1972).Google Scholar
9. Robertson, A. P. and Robertson, W. J., Topological vector spaces, 2nd edition (Cambridge University Press, London, 1973).Google Scholar
10. Robinson, A., Nonstandard analysis (North Holland, Amsterdam, 1968).Google Scholar
11. Robinson, A. and Zakon, E., A set-theoretical characterization of enlargements, Applications of model theory (Holt, Rinehart and Winston, New York, 1969), 109–122.Google Scholar
12. Terzioglu, T., On Schwartz spaces, Math. Ann. 182 (1969), 236–242.Google Scholar