Article contents
On Elliptically Embedded Subgroups of Soluble Groups
Published online by Cambridge University Press: 20 November 2018
Extract
We call a subset X of a group an elliptic set if there is an integer n such that each element of the group generated by X can be written as a product of at most n elements of X ∪ X−1. The terminology is due to Philip Hall, who investigated elliptic sets in lectures given in Cambridge in the 1960's. Hall was chiefly interested in sets X which are unions of conjugacy classes, but among other things he proved that if H, K are subgroups of a finitely generated nilpotent group then their union H ∪ K is elliptic. We shall say that a subgroup H of an arbitrary group G is elliptically embedded in G, and we write H ee G, if H ∪ K is an elliptic set for each subgroup K of G. Thus H ee G if for each subgroup K there is an integer n (depending on K) such that
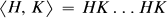
where the product has 2n factors.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1987
References
- 5
- Cited by


