Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T15:51:12.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On Dirichlet Spaces With a Class of Superharmonic Weights

Published online by Cambridge University Press:  20 November 2018

Guanlong Bao ,
Nihat Gokhan Göğüş  and
Stamatis Pouliasis
Guanlong Bao
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515063, China email: [email protected]
Nihat Gokhan Göğüş
Affiliation:
Faculty of Engineering and Natural Sciences, Sabanci University, Tuzla, Istanbul, 34956 Turkey email: [email protected]@gmail.com
Stamatis Pouliasis
Affiliation:
Faculty of Engineering and Natural Sciences, Sabanci University, Tuzla, Istanbul, 34956 Turkey email: [email protected]@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate Dirichlet spaces 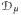${{D}_{\mu }}$ with superharmonic weights induced by positive Borel measures $\mu $ on the open unit disk. We establish the Alexander-Taylor-Ullman inequality for 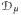${{D}_{\mu }}$ spaces and we characterize the cases where equality occurs. We define a class of weighted Hardy spaces 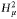$H_{\mu }^{2}$ via the balayage of the measure $\mu $ . We show that 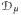${{D}_{\mu }}$ is equal to 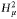$H_{\mu }^{2}$ if and only if $\mu $ is a Carleson measure for 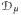${{D}_{\mu }}$ . As an application, we obtain the reproducing kernel of 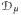${{D}_{\mu }}$ when $\mu $ is an infinite sum of point-mass measures. We consider the boundary behavior and innerouter factorization of functions in 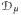${{D}_{\mu }}$. We also characterize the boundedness and compactness of composition operators on 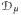${{D}_{\mu }}$.

Keywords

30H1031C2546E15Dirichlet spaceHardy spacesuperharmonic weight
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 721 - 741
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Alan, M. A. and Göğüş, N. G., Poletsky-Stessin-Hardy spaces in the plane. Complex Anal. Oper. Theory 8(2014), 975–990. http://dx.doi.Org/10.1007/s11785-013-0334-2 Google Scholar
[2] Aleman, A., Hilbert spaces of analytic functions between the Hardy and the Dirichlet space. Proc. Amer. Math. Soc. 115(1992), 97–104. http://dx.doi.org/10.1090/S0002-9939-1992-1079693-X Google Scholar
[3] Aleman, A., The multiplication operator on Hilbert spaces of analytic functions. Habilitation, Fern Universität Hagen, 1993.Google Scholar
[4] Alexander, H. and Osserman, R., Area bounds for various classes of surfaces. Amer. J. Math. 97(1975), 753–769. http://dx.doi.org/10.2307/2373775 Google Scholar
[5] Alexander, H., Taylor, B. A., and Ullman, J. L., Areas of projections of analytic sets. Invent. Math. 16(1972), 335–341. http://dx.doi.org/10.1007/BF01425717 Google Scholar
[6] Armitage, D. H. and Gardiner, S. J., Classical potential theory. Springer Monographs in Mathematics, Springer-Verlag, London, 2001.Google Scholar
[7] Bao, G., Lou, Z., Qian, R., and Wulan, H., On multipliers of Dirichlet type spaces. Complex Anal. Oper. Theory 9(2015), 1701–1732. http://dx.doi.Org/10.1007/s11785-015-0444-0 Google Scholar
[8] Bao, G., Lou, Z., Qian, R., and Wulan, H., On absolute values of QK functions. Bull. Korean Math. Soc. 53(2016), 561–568. http://dx.doi.Org/10.4134/BKMS.2016.53.2.561 Google Scholar
[9] Betsakos, D., Lindelöf's principle and estimates for holomorphic functions involving area, diameter, or integral means. Comput. Methods Funct. Theory 14(2014), 85–105. http://dx.doi.Org/10.1007/s40315-014-0049-z Google Scholar
[10] Bonilla, A., Pérez-González, F., Stray, A., and Trujillo-González, R., Approximation in weighted Hardy spaces. J. Anal. Math. 73(1997), 65–89. http://dx.doi.Org/10.1007/BF02788138 Google Scholar
[11] Costara, C., Reproducing kernels for Dirichlet spaces associated to finitely supported measures. Complex Anal. Oper. Theory 10(2016), 1277–1293. http://dx.doi.Org/10.1007/s11785-015-0510-7 Google Scholar
[12] Costara, C. and Ransford, T., Which de Branges-Rovnyak spaces are Dirichlet spaces (and vice versa)?. J. Funct. Anal. 265(2013), 3204–3218. http://dx.doi.Org/10.1016/j.jfa.2O13.08.015 Google Scholar
[13] Duren, P. L., Theory of Hp spaces, pure and Applied Mathematics, 38. Academic Press, New York, 1970; reprinted with supplement by Dover Publications, 2000.Google Scholar
[14] El-Fallah, O., Kellay, K., Klaja, H., Mashreghi, J., and Ransford, T., Dirichlet spaces with superharmonic weights and de Branges-Rovnyak spaces. Complex Anal. Oper. Theory 10(2016), 97–107. http://dx.doi.Org/10.1007/s11785-015-0474-7 Google Scholar
[15] El-Fallah, O., Kellay, K., Mashreghi, J., and Ransford, T., A Primer on the Dirichlet Space. Cambridge Tracts in Mathematics, 203, Cambridge University Press, Cambridge, 2014.Google Scholar
[16] Garnett, J. B., Bounded analytic functions. Graduate Texts in Mathematics, 236. Springer, New York, 2007.Google Scholar
[17] Girela, D., Pelaez, J. A., and Vukotic, D., Interpolating Blaschke products: Stolz and tangential approach regions. Constr. Approx. 27(2008), 203–216. http://dx.doi.org/10.1007/s00365-006-0651-6 Google Scholar
[18] Göğüş, N. G., Structure of weighted Hardy spaces in the plane, Filomat 30 (2016), 473–482. http://dx.doi.Org/1O.2298/FIL1602473C Google Scholar
[19] Kellay, K. and Lefèvre, P., Compact composition operators on weighted Hilbert spaces of analytic functions. J. Math. Anal. Appl. 386(2012), 718–727. http://dx.doi.Org/10.1016/j.jmaa.2011.08.033 Google Scholar
[20] Kerman, R. and Sawyer, E., Carleson measures and multipliers of Dirichlet-type spaces. Trans. Amer. Math. Soc. 309(1988), 87–98. http://dx.doi.org/!0.2307/2001160 Google Scholar
[21] Kobayashi, S., Range sets and BMO norms of analytic functions. Canad. J. Math. 36(1984), 747–755. http://dx.doi.org/10.4153/CJM-1984-042-6 Google Scholar
[22] Koosis, P., Introduction to Hp spaces. Second ed. with two appendices by Havin, V. P.. Cambridge University Press, Cambridge, 1998.Google Scholar
[23] Mashreghi, J., Derivatives of inner functions. Fields Institute Monographs, 31. Springer, New York, 2013. http://dx.doi.Org/10.1007/978-1-4614-5611-7 Google Scholar
[24] Ortega, J. and Fábrega, J., Pointwise multipliers and corona type decomposition in BMOA. Ann. Inst. Fourier (Grenoble) 46(1996), 111–137. http://dx.doi.Org/10.5802/aif.1509 Google Scholar
[25] Pau, J. and Pérez, P., Composition operators acting on weighted Dirichlet spaces. J. Math. Anal. Appl. 401(2013), 682–694. http://dx.doi.Org/10.1016/j.jmaa.2012.12.052 Google Scholar
[26] Poletsky, E. A. and Shrestha, K. R., On weighted Hardy spaces on the unit disk. In: Constructive approximation of functions. Banach Center Publ., 107. Polish Acad. Sci. Inst. Math., Warsaw, 2015, pp. 195–204. http://dx.doi.org/10.4064/bc107-0-14Google Scholar
[27] Poletsky, E. A. and Stessin, M. I., Hardy and Bergman spaces on hyperconvex domains and their composition operators. Indiana Univ. Math. J. 57(2008), 2153–2201. http://dx.doi.org/10.1512/iumj.2008.57.3360 Google Scholar
[28] Richter, S., A representation theorem for cyclic analytic two-isometries. Trans. Amer. Math. Soc. 328(1991), 325–349. http://dx.doi.Org/10.2307/2001885 Google Scholar
[29] Sahin, S., Poletsky-Stessin Hardy spaces on domains bounded by an analytic Jordan curve in ℂ. Complex Var. Elliptic Equ. 60(2015), 1114–1132. http://dx.doi.Org/10.1080/17476933.2014.1001112 Google Scholar
[30] Sakai, M., Isoperimetric inequalities for the least harmonic majorant of |x|p . Trans. Amer. Math. Soc. 299(1987), 431–472. http://dx.doi.org/10.2307/2000507 Google Scholar
[31] Sarason, D. and Silva, J-N. O., Composition operators on a local Dirichlet space. J. Anal. Math. 87(2002), 433–450. http://dx.doi.org/10.1007/BF02868484 Google Scholar
[32] Shapiro, J. H., Composition operators and classical function theory. Universitext: Tracts in Mathematics. Springer-Verlag, New York, 1993. http://dx.doi.Org/10.1007/978-1-4612-0887-7 Google Scholar
[33] Shimorin, S. M., Reproducing kernels and extremal functions in Dirichlet-type spaces. (Russian) Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI), 255(1998), 198–220. 254. Translation in J. Math. Sci. 107(2001), 4108-4124. http://dx.doi.Org/10.1023/A:1012453003423 Google Scholar
[34] Shimorin, S. M., Complete Nevanlinna-Pick property of Dirichlet-type spaces. J. Funct. Anal. 191(2002), 276–296. http://dx.doi.org/10.1006/jfan.2001.3871 Google Scholar
[35] Shrestha, K. R., Boundary values properties of functions in weighted Hardy spaces. arxiv:1309.6561.Google Scholar
[36] Stanton, C. S., Isoperimetric inequalities and Hp estimates. Complex Variables Theory Appl. 12(1989), 17–21.Google Scholar
[37] Tjani, M., Compact composition operators on Besov spaces. Trans. Amer. Math. Soc. 355(2003), 4683–4698. http://dx.doi.org/10.1090/S0002-9947-03-03354-3 Google Scholar
[38] Xiao, J., Holomorphic Q classes. Lecture Notes in Mathematics, 1767. Springer-Verlag, Berlin, 2001. http://dx.doi.Org/10.1007/b87877 Google Scholar