Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-19T01:44:04.743Z Has data issue: false hasContentIssue false
  • English
  • Français

On Cabled Knots and Vassiliev Invariants (Not) Contained in Knot Polynomials

Published online by Cambridge University Press:  20 November 2018

A. Stoimenow
A. Stoimenow*
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto 606-8502, Japan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

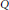It is known that the Brandt–Lickorish–Millett–Ho polynomial $Q$ contains Casson's knot invariant. Whether there are (essentially) other Vassiliev knot invariants obtainable from 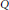$Q$ is an open problem. We show that this is not so up to degree 9. We also give the (apparently) first examples of knots not distinguished by 2-cable HOMFLY polynomials which are not mutants. Our calculations provide evidence of a negative answer to the question whether Vassiliev knot invariants of degree 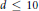$d\,\le \,10$ are determined by the HOMFLY and Kauffman polynomials and their 2-cables, and for the existence of algebras of such Vassiliev invariants not isomorphic to the algebras of their weight systems.

Keywords

57M2557M2720F3657M50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 2 , 01 April 2007 , pp. 418 - 448
Copyright
Copyright © Canadian Mathematical Society 2007

References

[Ad] Adams, C. C., Das Knotenbuch. Spektrum Akademischer Verlag, Berlin, 1995 (The knot book, W. H. Freeman & Co., New York, 1994).Google Scholar
[Al] Alexander, J. W., Topological invariants of knots and links. Trans. Amer. Math. Soc. 30(1928), 275–306.Google Scholar
[APR] Anstee, R. P., Przytycki, J. H. and Rolfsen, D., Knot polynomials and generalized mutation. Topology Appl. 32(1989), no. 3, 237–249.Google Scholar
[BN] Bar-Natan, D., On the Vassiliev knot invariants. Topology 34(1995), no. 2, 423–472.Google Scholar
[BN2] Bar-Natan, D., Polynomial invariants are polynomial. Math. Res. Lett. 2(1995), no. 3, 239–246.Google Scholar
[BG] Bar-Natan, D. and Garoufalidis, S., On the Melvin-Morton-Rozansky Conjecture. Invent. Math. 125(1996), no. 1, 103–133.Google Scholar
[BS] Bar-Natan, D. and Stoimenow, A., The fundamental theorem of Vassiliev invariants. In: Geometry and Physics, Lecture Notes in Pure and Appl. Math. 184, Dekker, New York, 1996, pp. 101–134.Google Scholar
[Bi] Birman, J. S., New points of view in knot theory. Bull. Amer. Math. Soc. 28(1993), no. 2, 253–287.Google Scholar
[BL] Birman, J. S. and Lin, X.-S., Knot polynomials and Vassiliev's invariants. Invent. Math. 111(1993), no. 2, 225–270.Google Scholar
[BLM] Brandt, R. D., Lickorish, W. B. R. and Millett, K., A polynomial invariant for unoriented knots and links. Invent. Math. 84(1986), no. 3, 563–573.Google Scholar
[CD] Chmutov, S. V. and Duzhin, S. V., An upper bound for the number of Vassiliev knot invariants. J. Knot Theory Ramifications, 3(2)(1994), no. 2, 141–151.Google Scholar
[CDL] Chmutov, S. V., Duzhin, S. V. and Lando, S. K., Vassiliev knot invariants. I. Introduction. In: Singularities and Bifurcations, Adv. Soviet Math. 21, American Mathematical Society, Providence, RI, 1994, pp. 117–126.Google Scholar
[CDL2] Chmutov, S. V., Duzhin, S. V. and Lando, S. K., Vassiliev knot invariants. II. Intersection graph conjecture for trees. In: Singularities and Bifurcations, Adv. Soviet Math. 21, American Mathematical Society, Providence, RI, 1994, pp. 127–134.Google Scholar
[CJP] Choi, Y., Jeong, M. J. and Park, C. Y., Twist of knots and the Q-polynomials. Kyungpook Math. J. 44(3)(2004), no. 3, 449–467.Google Scholar
[Co] Conway, J. H., An enumeration of knots and links and some of their algebraic properties. In: Computational Problems in Abstract Algebra, Pergamon, Oxford, 1969, pp. 329–358.Google Scholar
[Da] Dasbach, O. T., On the combinatorial structure of primitive Vassiliev invariants. III. A lower bound. Commun. Contemp. Math. 2(2000), no. 4, 579–590.Google Scholar
[De] Dean, J., Many classical knot invariants are not Vassiliev invariants. J. Knot Theory Ramifications 3(1994), no. 1, 7–10.Google Scholar
[Ei] Eisermann, M., The number of knot group representations is not a Vassiliev invariant. Proc. Amer. Math. Soc. 128(2000), no. 5, 1555–1561.Google Scholar
[Ei2] Eisermann, M., A geometric characterization of Vassiliev invariants. Trans. Amer. Math. Soc. 355(2003), no. 12, 4825–4846.Google Scholar
[FW] Franks, J. and Williams, R. F., Braids and the Jones polynomial. Trans. Amer. Math. Soc. 303(1987), no. 1, 97–108.Google Scholar
[FY] Freyd, P., Yetter, D., Hoste, J., Lickorish, W. B. R., Millett, K., and Ocneanu, A., A new polynomial invariant of knots and links. Bull. Amer. Math. Soc. 12(1985), no. 2, 239–246.Google Scholar
[HS] Hirasawa, M. and Stoimenow, A., Examples of knots without minimal string Bennequin surfaces. Asian J. Math. 7(2003), no. 3, 435–445.Google Scholar
[Ho] Ho, C. F., A polynomial invariant for knots and links – preliminary report. Abstracts Amer. Math. Soc. 6(1985), 300.Google Scholar
[HP] Hoste, J. and Przytycki, J., Tangle surgeries which preserve Jones-type polynomials. Internat. J. Math. 8(1997), no. 8, 1015–1027.Google Scholar
[HT] Hoste, J. and Thistlethwaite, M., KnotScape, a knot polynomial calculation program, available at http://www.math.utk.edu/∼morwen. Google Scholar
[JR] Jin, G. T. and Rolfsen, D., Some remarks on rotors in link theory. Canad. Math. Bull. 34(1991), no. 4, 480–484.Google Scholar
[J] Jones, V. F. R., A polynomial invariant of knots and links via von Neumann algebras. Bull. Amer. Math. Soc. 12(1985), no. 1, 103–111.Google Scholar
[K] Kanenobu, T., An evaluation of the first derivative of the Q polynomial of a link. Kobe J. Math. 5(1988), no. 2, 179–184.Google Scholar
[K2] Kanenobu, T., Relations between the Jones and Q polynomials for 2-bridge and 3-braid links. Math. Ann. 285(1989), no. 1, 115–124.Google Scholar
[K3] Kanenobu, T., Kauffman polynomials and Vassiliev link invariants. In: Knots 96, World Scientific Publishing, 1997, pp. 411–431.Google Scholar
[K4] Kanenobu, T., Vassiliev knot invariants of order 6. J. Knot Theory Ramifications 10(2001), no. 5, 645–665.Google Scholar
[KM] Kanenobu, T. and Miyazawa, Y., HOMFLY polynomials as Vassiliev link invariants. In: Knot Theory, Banach Center Publications 42, Polish Acad. Sci., Warsaw, 1998, pp. 165–185.Google Scholar
[Ks] Kassel, C., Quantum Groups. Graduate Texts in Mathematics 155, Springer-Verlag, New York, 1995.Google Scholar
[Ka] Kauffman, L. H., State models and the Jones polynomial. Topology 26(1987), no. 3, 395–407.Google Scholar
[Ka2] Kauffman, L. H., An invariant of regular isotopy. Trans. Amer. Math. Soc. 318(1990), no. 2, 417–471.Google Scholar
[Kh] Khovanov, M., A categorification of the Jones polynomial. Duke Math. J. 101(2000), no. 3, 359–426.Google Scholar
[KS] Kidwell, M. and Stoimenow, A., Examples relating to the crossing number, writhe, and maximal bridge length of knot diagrams. Mich. Math. J. 51(2003), no. 1, 3–12.Google Scholar
[Ki] Kirby, R. (ed.), Problems of low-dimensional topology, book available at http://math.berkeley.edu/∼kirby. Google Scholar
[Kn] Kneissler, J., The number of primitive Vassiliev invariants up to degree 12. Preprint math.QA/9706022.Google Scholar
[Ko] Kontsevich, M., Vassiliev's knot invariants. Adv. Sov. Math. 16, American Mathematical Society, Providence, RI, 1993, pp. 137–150.Google Scholar
[KSA] Kricker, A., Spence, B. and Aitchison, I., Cabling the Vassiliev invariants. J. Knot Theory Ramifications 6(1997), no. 3, 327–358.Google Scholar
[LMr] Le, T. and Murakami, J., Kontsevich's integral for the Homfly polynomial and relations between multiple zeta functions. Topology Appl. 62(1995), no. 2, 193–206.Google Scholar
[LMr2] Le, T. and Murakami, J., Kontsevich's integral for the Kauffman polynomials. Nagoya Math. J. 142(1996), 39–66.Google Scholar
[LMr3] Le, T. and Murakami, J., The universal Vassiliev-Kontsevich invariant for framed oriented links. Compositio Math. 102(1996), no. 1, 41–64.Google Scholar
[L] Lickorish, W. B. R., The panorama of polynomials of knots, links and skeins. In: Braids, Contemp. Math. 78, American Mathematical Society, Providence, RI, 1988, pp. 399–414.Google Scholar
[LL] Lickorish, W. B. R. and Lipson, A. S., Polynomials of 2-cable-like links. Proc. Amer. Math. Soc. 100(1987), no. 2, 355–361.Google Scholar
[LM] Lickorish, W. B. R. and Millett, K. C., A polynomial invariant of oriented links. Topology 26(1987), no. 1, 107–141.Google Scholar
[Li] Lieberum, J., The number of independent Vassiliev invariants in the Homfly and Kauffman polynomials. Doc. Math. 5(2000), 275–299.Google Scholar
[LW] Lin, X.-S. and Wang, Z., Integral geometry of plane curves and knot invariants. J. Differential Geom. 44(1996), no. 1, 74–95.Google Scholar
[MR] McDaniel, M. and Rong, Y., Vassiliev invariants from satellites of link polynomials. Kobe J. Math. 18(2001), no. 2, 127–145.Google Scholar
[Me] Meng, G., Bracket models for weight systems and the universal Vassiliev invariants. Topology Appl. 76(1997), no. 1, 47–60.Google Scholar
[Mo] Morton, H. R., Seifert circles and knot polynomials. Math. Proc. Cambridge Philos. Soc. 99(1986), no. 1, 107–109.Google Scholar
[MS] Morton, H. R. and Short, H. B., The 2-variable polynomial of cable knots. Math. Proc. Camb. Philos. Soc. 101(1987), no. 2, 267–278.Google Scholar
[MC] Morton, H. R. and Cromwell, P. R., Distinguishing mutants by knot polynomials. J. Knot Theory Ramifications 5(1996), no. 2, 225–238.Google Scholar
[Mr] Murakami, J., Finite type invariants detecting the mutant knots. In: “Knot theory”, Dedicated to Prof. K. Murasugi for his 70th birthday, Sakuma, M. et al. (Eds.), Osaka University, 2000, pp. 258–267. Available at http://www.f.waseda.jp/murakami/papers/finitetype.pdf. Google Scholar
[Mu] Murasugi, K., Classical numerical invariants in knot theory. In: Topics in Knot Theory, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 399, Kluwer Acad. Publ., Dordrecht, 1993, pp. 157–194.Google Scholar
[Mu2] Murasugi, K., On the braid index of alternating links. Trans. Amer. Math. Soc. 326(1991), no. 1, 237–260.Google Scholar
[Oh] Ohyama, Y., On the minimal crossing number and the braid index of links. Canad. J. Math. 45(1993), no. 1, 117–131.Google Scholar
[PV] Polyak, M. and Viro, O., Gauss diagram formulas for Vassiliev invariants. Internat. Math. Res. Notices 11(1994), 445–454.Google Scholar
[Ro] Rolfsen, D., Knots and Links. Mathematics Lecture Series 7, Publish or Parish, Houston, TX, 1976.Google Scholar
[Ru] Ruberman, D.,Mutation and volumes of knots in S3 . Invent. Math. 90(1987), no. 1, 189–215.Google Scholar
[Sh] Schubert, H., Knoten mit zwei Brücken. Math. Z. 65(1956), 133–170.Google Scholar
[S] Stanford, T., Computing Vassiliev's invariants. Topology Appl. 77(1997), no. 3, 261–276.Google Scholar
[St] Stoimenow, A., Gauss sum invariants, Vassiliev invariants and braiding sequences. J. Knot Theory Ramifications 9(2000), no. 2, 221–269.Google Scholar
[St2] Stoimenow, A., Polynomial and polynomially growing knot invariants. Preprint, http://www.kurims.kyoto-u.ac.jp/∼stoimeno/papers/beha.ps.gz. Google Scholar
[St3] Stoimenow, A., Polynomials of knots with up to 10 crossings. Tables available at http://www.kurims.kyoto-u.ac.jp/∼stoimeno/ptab/. Google Scholar
[St4] Stoimenow, A., Vassiliev invariants on fibered and mutually obverse knots. J. Knot Theory Ramifications 8(1999), no. 4, 511–519.Google Scholar
[St5] Stoimenow, A., Positive knots, closed braids, and the Jones polynomial. Ann. Sc. Norm. Super. Pisa Cl. Sci. 2(2003), no. 2, 237–285.Google Scholar
[St6] Stoimenow, A., A note on Vassiliev invariants not contained in the knot polynomials. C. R. Acad. Bulgare Sci. 54(2001), no. 4, 9–14.Google Scholar
[St7] Stoimenow, A., On finiteness of Vassiliev invariants and a proof of the Lin-Wang conjecture via braiding polynomials. J. Knot Theory Ramifications 10(2001), no. 5, 769–780.Google Scholar
[St8] Stoimenow, A., On the crossing number of positive knots and braids and braid index criteria of Jones and Morton-Williams-Franks. Trans. Amer. Math. Soc. 354(2002), no. 10, 3927–3954.Google Scholar
[Tz] Traczyk, P., A note on rotant links. J. Knot Theory Ramifications 8(1999), no. 3, 397–403.Google Scholar
[Tr] Trapp, R., Twist sequences and Vassiliev invariants. J. Knot Theory Ramifications 3(1994), no. 3, 391–405.Google Scholar
[Va] Vassiliev, V. A., Cohomology of knot spaces. In: Theory of Singularities and its Applications, Adv. Soviet Math. 1, American Mathematical Society, Providence, RI, 1990, pp. 23–69.Google Scholar
[Vo] Vogel, P., Algebraic structures on modules of diagrams. http://www.math.jussieu.fr/_vogel. Google Scholar
[Y] Yamada, S., An operator on regular isotopy invariants of link diagrams. Topology 28(3)(1989), 369–377.Google Scholar