No CrossRef data available.
Article contents
On Algebraic Surfaces Associated with Line Arrangements
Published online by Cambridge University Press: 07 January 2019
Abstract
For a line arrangement 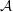 ${\mathcal{A}}$ in the complex projective plane
${\mathcal{A}}$ in the complex projective plane 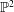 $\mathbb{P}^{2}$, we investigate the compactification
$\mathbb{P}^{2}$, we investigate the compactification 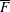 $\overline{F}$ in
$\overline{F}$ in 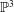 $\mathbb{P}^{3}$ of the affine Milnor fiber
$\mathbb{P}^{3}$ of the affine Milnor fiber 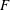 $F$ and its minimal resolution
$F$ and its minimal resolution 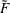 $\tilde{F}$. We compute the Chern numbers of
$\tilde{F}$. We compute the Chern numbers of 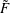 $\tilde{F}$ in terms of the combinatorics of the line arrangement
$\tilde{F}$ in terms of the combinatorics of the line arrangement 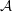 ${\mathcal{A}}$. As applications of the computation of the Chern numbers, we show that the minimal resolution is never a quotient of a ball; in addition, we also prove that
${\mathcal{A}}$. As applications of the computation of the Chern numbers, we show that the minimal resolution is never a quotient of a ball; in addition, we also prove that 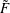 $\tilde{F}$ is of general type when the arrangement has only nodes or triple points as singularities. Finally, we compute all the Hodge numbers of some
$\tilde{F}$ is of general type when the arrangement has only nodes or triple points as singularities. Finally, we compute all the Hodge numbers of some 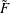 $\tilde{F}$ by using some knowledge about the Milnor fiber monodromy of the arrangement.
$\tilde{F}$ by using some knowledge about the Milnor fiber monodromy of the arrangement.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018


