Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T15:30:42.377Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Generalized Fundamental Equation of Information

Published online by Cambridge University Press:  20 November 2018

Pl. Kannappan  and
C. T. Ng
Pl. Kannappan
Affiliation:
University of Waterloo, Waterloo, Ontario
C. T. Ng
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The object of this paper is to determine the general solution of the functional equation

FE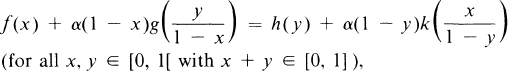

where α is multiplicative. It turns out that non-trivial embeddings of the reals in the complex generate some interesting solutions.

In many applications, various special cases of (FE) have occurred ([1,3, 4, 6, 10, 11, 14]). The special case where f = g = h = k and α = the identity map is known as the fundamental equation of information, and has been extensively investigated by many authors ([5]). The case where f = g = h = k and α is multiplicative was treated in [13, 14]. The general solution of (FE) when α(1 – x) = (1 – x)β has been obtained in [9], except when β = 2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 862 - 872
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Aczél, J., Notes on generalized information functions, Aeq. Math. 22 (1981), 97–107.Google Scholar
2. Aczél, J., Derivation and information functions, (A tale of two surprises and a half) (Contributions to Probability, Academic Press, 1981).Google Scholar
3. Aczél, J., Forte, B. and Ng, C. T., Why the Shannon and Hartley entropies are natural, Adv. Appl. Prob. 6 (1974), 131–146.Google Scholar
4. Aczél, J. and Kannappan, PL., A mixed theory of information III. Inset entropies of degree β, Information and Control 34 (1978), 315–322.Google Scholar
5. Aczél, J. and Daroczy, Z., On measures of information and their characterizations (Academic Press, New York, 1975).Google Scholar
6. Aczél, J. and Daroczy, Z., A mixed theory of information I., Symmetric, recursive and measurable entropies of randomized systems of events, RAIRO Informat. Theor. 12 (1978), 149–155.Google Scholar
7. Horinouchi, S. and Kannappan, PL., On a system of functional equations f(x + y) = f(x) + f(y) andf(xy) = p(x)f(y) + q(y)f(x), Aeq. Math. 6 (1971), 195–201.Google Scholar
8. Jacobson, N., Lectures in abstract algebra, Vol. 3 (Chapter 6) (Van Nostrand, 1964).Google Scholar
9. Kannappan, PL., Notes on generalized information function, Tohoku Math. J. 30 (1978), 251–255.Google Scholar
10. Kannappan, PL. and Ng, C. T., Measurable solutions of functional equations related to information theory, Proc. Amer. Math. Soc. 38 (1973), 303–310.Google Scholar
11. Maksa, Gy, The general solution of a functional equation related to mixed theory of information, Aeq. Math. 22 (1981), 90–96.Google Scholar
12. Maksa, Gy, Solution on the open triangle of the generalized fundamental equation of information with four unknown functions (Utilitas Math.)Google Scholar
13. Ng, C. T., Information functions on open domains I and II, C. R. Math. Rep. Acad. Sci. Canada 2 (1980), 119-123 and 155–158.Google Scholar
14. Rathie, P. N. and Kannappan, PL., On a functional equation connected with Shannon's entropy, Funkcial. Ekvoc. 14 (1971), 38–45.Google Scholar
15. Vincze, E., Eine allgemeinere Méthode in der Théorie der Funktionalgleichungen, III, Publ. Math. Debrecen 70 (1963), 191–202.Google Scholar
16. Zariski, O. and Samuel, P., Commutative algebra, Vol. I (Van Nostrand, Princeton, N.J., 1958).Google Scholar