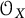1 Introduction
The Cuntz–Pimsner
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_X$
is an invariant of conjugacy associated with any shift space X. This interplay between shift spaces and
$\mathcal {O}_X$
is an invariant of conjugacy associated with any shift space X. This interplay between shift spaces and
![]() $C^*$
-algebras starts from the study of the
$C^*$
-algebras starts from the study of the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_A$
of a two-sided shift of finite type represented by a
$\mathcal {O}_A$
of a two-sided shift of finite type represented by a
![]() $\{0,1\}$
-matrix A in a canonical way (see [Reference Cuntz and Krieger11]), in which the associated
$\{0,1\}$
-matrix A in a canonical way (see [Reference Cuntz and Krieger11]), in which the associated
![]() $C^*$
-algebra is originally called a Cuntz–Krieger algebra. In the next 30 years, the
$C^*$
-algebra is originally called a Cuntz–Krieger algebra. In the next 30 years, the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_X$
, to every shift space X, is constructed and studied in [Reference Bates, Carlsen and Eilers1, Reference Carlsen5, Reference Carlsen7–Reference Carlsen and Matsumoto9, Reference Katayama, Matsumoto and Watatani13, Reference Krieger and Matsumoto14, Reference Matsumoto16–Reference Matsumoto18] by several authors (for example, Matsumoto, Eilers, Carlsen, Brix, and their collaborators, to name a few), but in different manners for their own uses. We additionally remark that the associated
$\mathcal {O}_X$
, to every shift space X, is constructed and studied in [Reference Bates, Carlsen and Eilers1, Reference Carlsen5, Reference Carlsen7–Reference Carlsen and Matsumoto9, Reference Katayama, Matsumoto and Watatani13, Reference Krieger and Matsumoto14, Reference Matsumoto16–Reference Matsumoto18] by several authors (for example, Matsumoto, Eilers, Carlsen, Brix, and their collaborators, to name a few), but in different manners for their own uses. We additionally remark that the associated
![]() $C^*$
-algebra considered in the paper is first defined by Carlsen in [Reference Carlsen7] using a Cuntz–Pimsner construction, which is why we call it a Cuntz–Pimsner
$C^*$
-algebra considered in the paper is first defined by Carlsen in [Reference Carlsen7] using a Cuntz–Pimsner construction, which is why we call it a Cuntz–Pimsner
![]() $C^*$
-algebra, as is also pointed out in [Reference Brix and Carlsen4].
$C^*$
-algebra, as is also pointed out in [Reference Brix and Carlsen4].
Among these approaches, the cover
![]() $(\tilde {X},\sigma _{\widetilde {X}})$
, of a one-sided shift space X, is a dynamical system constructed by Carlsen in [Reference Brix and Carlsen4], and used to define the
$(\tilde {X},\sigma _{\widetilde {X}})$
, of a one-sided shift space X, is a dynamical system constructed by Carlsen in [Reference Brix and Carlsen4], and used to define the
![]() $\mathcal {O}_X$
as the full groupoid
$\mathcal {O}_X$
as the full groupoid
![]() $C^*$
-algebra of
$C^*$
-algebra of
![]() $\mathcal {G}_{\tilde {X}}$
. In particular, the reason why Carlsen considers the groupoid
$\mathcal {G}_{\tilde {X}}$
. In particular, the reason why Carlsen considers the groupoid
![]() $C^*$
-algebra of the cover but not the shift space X itself is that every such cover defines a dynamical system whose underlying map is a local homeomorphism, whereas this is not always the case for a one-sided shift. Actually, a one-sided shift on an infinite space is a local homeomorphism if and only if it is of finite type, as in [Reference Parry19].
$C^*$
-algebra of the cover but not the shift space X itself is that every such cover defines a dynamical system whose underlying map is a local homeomorphism, whereas this is not always the case for a one-sided shift. Actually, a one-sided shift on an infinite space is a local homeomorphism if and only if it is of finite type, as in [Reference Parry19].
In [Reference Carlsen6], it is shown that for every shift space X with the property (*), there is a surjective homomorphism
![]() $ \rho : \mathcal {O}_X\to C(\underline {X})\rtimes _{\sigma }\mathbb {Z}$
, which sends the diagonal subalgebra
$ \rho : \mathcal {O}_X\to C(\underline {X})\rtimes _{\sigma }\mathbb {Z}$
, which sends the diagonal subalgebra
![]() $\mathcal {D}_X$
onto the canonical commutative
$\mathcal {D}_X$
onto the canonical commutative
![]() $C^*$
-subalgebra
$C^*$
-subalgebra
![]() $C(\underline {X})$
, with
$C(\underline {X})$
, with
![]() $\underline {X}$
the corresponding two-sided shift space of X and
$\underline {X}$
the corresponding two-sided shift space of X and
![]() $\sigma $
the natural two-sided shift operation. In addition, if X has the property (**), then
$\sigma $
the natural two-sided shift operation. In addition, if X has the property (**), then
where
![]() $\textbf {n}_X$
is a positive integer related to the structure of the left special elements in X, namely, the number of right shift tail equivalence classes of X containing a left special element. Consequently, for every minimal shift space X, if it has the property (**), which is equivalent to X having finitely many left special elements, then its Cuntz–Pimsner
$\textbf {n}_X$
is a positive integer related to the structure of the left special elements in X, namely, the number of right shift tail equivalence classes of X containing a left special element. Consequently, for every minimal shift space X, if it has the property (**), which is equivalent to X having finitely many left special elements, then its Cuntz–Pimsner
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_X$
is an extension of a unital simple A
$\mathcal {O}_X$
is an extension of a unital simple A
![]() $\mathbb {T}$
-algebra by a finite direct sum of the compact operators. Also note that this extension makes
$\mathbb {T}$
-algebra by a finite direct sum of the compact operators. Also note that this extension makes
![]() $\mathcal {O}_X$
falls into a class of
$\mathcal {O}_X$
falls into a class of
![]() $C^*$
-algebras considered by Lin and Su in [Reference Lin and Su15], called the direct limits of generalized Toeplitz algebras.
$C^*$
-algebras considered by Lin and Su in [Reference Lin and Su15], called the direct limits of generalized Toeplitz algebras.
In [Reference Brix3], Brix considers the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_{\alpha }$
of a one-sided Sturmian shift
$\mathcal {O}_{\alpha }$
of a one-sided Sturmian shift
![]() $X_\alpha $
for
$X_\alpha $
for
![]() ${\alpha }$
an irrational number, by describing the cover of
${\alpha }$
an irrational number, by describing the cover of
![]() $X_{\alpha }$
. In particular, he proves that the cover
$X_{\alpha }$
. In particular, he proves that the cover
![]() $\widetilde {X}_{\alpha }$
of
$\widetilde {X}_{\alpha }$
of
![]() $X_{\alpha }$
is a union of the two-sided Sturmian shift
$X_{\alpha }$
is a union of the two-sided Sturmian shift
![]() $\underline {X_{\alpha }}$
and a dense orbit consisting of isolated points. The unique dense orbit corresponds to the unique point
$\underline {X_{\alpha }}$
and a dense orbit consisting of isolated points. The unique dense orbit corresponds to the unique point
![]() $\omega _{\alpha }$
in
$\omega _{\alpha }$
in
![]() $X_{\alpha }$
, which has two preimages under the shift operation. This is the first concrete description of covers of non-sofic systems, whereas the cover of a sofic system is a specific class of shifts of finite type. We remark here that the uniqueness of
$X_{\alpha }$
, which has two preimages under the shift operation. This is the first concrete description of covers of non-sofic systems, whereas the cover of a sofic system is a specific class of shifts of finite type. We remark here that the uniqueness of
![]() $\omega _{\alpha }$
benefits from the well-known fact that
$\omega _{\alpha }$
benefits from the well-known fact that
![]() $X_{\alpha }$
has the smallest complexity growth for shift spaces with no ultimately periodic points:
$X_{\alpha }$
has the smallest complexity growth for shift spaces with no ultimately periodic points:
![]() $p_{X}(n)=n+1$
for all
$p_{X}(n)=n+1$
for all
![]() $n\ge 1$
.
$n\ge 1$
.
There are two corollaries from the concrete description of the cover of a Sturmian system in [Reference Brix3]: one for a reducing of the exact sequence in [Reference Carlsen6] to its simplest form, that is,
![]() $\mathcal {O}_{\alpha }$
is an extension of
$\mathcal {O}_{\alpha }$
is an extension of
![]() $C(\underline {X_{\alpha }})\rtimes _\sigma \mathbb {Z}$
by
$C(\underline {X_{\alpha }})\rtimes _\sigma \mathbb {Z}$
by
![]() $\mathbb {K}$
; one for the precise value of dynamic asymptotic dimension of the associated groupoid. The latter together with the exact sequence make the
$\mathbb {K}$
; one for the precise value of dynamic asymptotic dimension of the associated groupoid. The latter together with the exact sequence make the
![]() $\mathcal {O}_{\alpha }$
be of nuclear dimension
$\mathcal {O}_{\alpha }$
be of nuclear dimension
![]() $1$
, where the nuclear dimension is a concept that plays a key role in the classification programs for
$1$
, where the nuclear dimension is a concept that plays a key role in the classification programs for
![]() $C^*$
-algebras.
$C^*$
-algebras.
In this note, we generalize this interesting approach and show that for every minimal one-sided shift X with finitely many left special elements, the Cuntz–Pimsner algebra
![]() $\mathcal {O}_X$
has nuclear dimension
$\mathcal {O}_X$
has nuclear dimension
![]() $1$
. More specifically, with our concrete description, the cover of each such space will be a finite disjoint union: a copy of the corresponding minimal two-sided shift space
$1$
. More specifically, with our concrete description, the cover of each such space will be a finite disjoint union: a copy of the corresponding minimal two-sided shift space
![]() $\underline {X}$
(induced from the projection limit of the original one-sided shift), and
$\underline {X}$
(induced from the projection limit of the original one-sided shift), and
![]() $\textbf {n}_X$
dense orbits, each consisting of isolated points. This also recovers the whole situation of the exact sequence in [Reference Carlsen6]. We also hope that with this description, more K-information can be read out from the groupoid for many other minimal shifts, such as nonperiodic Toeplitz shifts X with lower complexity growth (which is to sufficiently make X have finitely many left special elements, or equivalently, have the property (**)).
$\textbf {n}_X$
dense orbits, each consisting of isolated points. This also recovers the whole situation of the exact sequence in [Reference Carlsen6]. We also hope that with this description, more K-information can be read out from the groupoid for many other minimal shifts, such as nonperiodic Toeplitz shifts X with lower complexity growth (which is to sufficiently make X have finitely many left special elements, or equivalently, have the property (**)).
Finally, we also want to emphatically point out that there is a large class of minimal shifts for which our results apply, such as those with bounded complexity growth (see Example 3.15 for the definition and Proposition 3.16 for details). This class of minimal shifts includes minimal Sturmian shifts considered by Brix, which are defined to be the minimal shifts associated with irrational rotations; minimal shifts associated with interval exchange transformations, whose complexity functions are known to satisfy
![]() $p_X(n+1)-p_X(n)\leq d$
where d is the number of subintervals; minimal shifts constructed from
$p_X(n+1)-p_X(n)\leq d$
where d is the number of subintervals; minimal shifts constructed from
![]() $(p,q)$
-Toeplitz words in [Reference Cassaigne and Karhumäki10], where
$(p,q)$
-Toeplitz words in [Reference Cassaigne and Karhumäki10], where
![]() $p,q$
are natural numbers and
$p,q$
are natural numbers and
![]() $p|q$
, whose complexity functions are shown to be linear; or also minimal shifts associated with a class of translations on
$p|q$
, whose complexity functions are shown to be linear; or also minimal shifts associated with a class of translations on
![]() $2$
-torus in [Reference Berthé, Steiner and Thuswaldner2], whose complexity functions satisfy
$2$
-torus in [Reference Berthé, Steiner and Thuswaldner2], whose complexity functions satisfy
![]() $p_X(n)=2n+1$
, to name a few.
$p_X(n)=2n+1$
, to name a few.
1.1 Outline of the paper
The paper is organized as follows. Section 2 will provide definitions, including basic notions of one-sided shift spaces, the corresponding two-sided shift spaces, and
![]() $C^*$
-algebras. In Section 3, we recall definitions of past equivalence, right tail equivalence, covers, and their properties. A couple of technical preparations will also be presented for the later use. Section 4 is devoted to the main body of the paper, in which we give a concrete description to the cover of a minimal shift with finitely many left special elements. We divide the description into three parts: (i) for isolated points in the cover, see Theorem 4.1; (ii) for the surjective factor
$C^*$
-algebras. In Section 3, we recall definitions of past equivalence, right tail equivalence, covers, and their properties. A couple of technical preparations will also be presented for the later use. Section 4 is devoted to the main body of the paper, in which we give a concrete description to the cover of a minimal shift with finitely many left special elements. We divide the description into three parts: (i) for isolated points in the cover, see Theorem 4.1; (ii) for the surjective factor
![]() $\pi _X$
, see Theorems 4.6 and 4.7; and (iii) for nonisolated points in the cover, see Theorem 4.8. Finally, we conclude our main result for the nuclear dimension of
$\pi _X$
, see Theorems 4.6 and 4.7; and (iii) for nonisolated points in the cover, see Theorem 4.8. Finally, we conclude our main result for the nuclear dimension of
![]() $\mathcal {O}_X$
in Section 5.
$\mathcal {O}_X$
in Section 5.
2 Preliminaries
Throughout the paper, we denote by
![]() $\mathbb {N}$
the set of nonnegative integers. For a finite set S, we will always use
$\mathbb {N}$
the set of nonnegative integers. For a finite set S, we will always use
![]() $\#S$
to denote its cardinality.
$\#S$
to denote its cardinality.
2.1 Shift spaces
Let
![]() $\mathcal {A}=\{0,1\}$
. Endowed with the product topology, the spaces
$\mathcal {A}=\{0,1\}$
. Endowed with the product topology, the spaces
![]() $\mathcal {A}^{\mathbb {Z}}$
and
$\mathcal {A}^{\mathbb {Z}}$
and
![]() $\mathcal {A}^{\mathbb {N}}$
are homeomorphic to the Cantor space, i.e., the totally disconnected compact metric space with no isolated point. Note that
$\mathcal {A}^{\mathbb {N}}$
are homeomorphic to the Cantor space, i.e., the totally disconnected compact metric space with no isolated point. Note that
![]() $\mathcal {A}^{\mathbb {Z}}$
and
$\mathcal {A}^{\mathbb {Z}}$
and
![]() $\mathcal {A}^{\mathbb {N}}$
can be given the following metrics:
$\mathcal {A}^{\mathbb {N}}$
can be given the following metrics:
 $$ \begin{align*} \underline{d}(\underline{x},\underline{y})&=\sup\{1/2^N: \underline{x}_k=\underline{y}_k\ \mathrm{for\ all}\ 0\leq |k|\leq N-1\},\\ d(x,y)&=\sup\{1/2^N: x_k=y_k \ \mathrm{for\ all}\ 0\leq k\leq N-1\}. \end{align*} $$
$$ \begin{align*} \underline{d}(\underline{x},\underline{y})&=\sup\{1/2^N: \underline{x}_k=\underline{y}_k\ \mathrm{for\ all}\ 0\leq |k|\leq N-1\},\\ d(x,y)&=\sup\{1/2^N: x_k=y_k \ \mathrm{for\ all}\ 0\leq k\leq N-1\}. \end{align*} $$
We use
![]() $\mathcal {A}^*$
and
$\mathcal {A}^*$
and
![]() $\mathcal {A}^\infty $
to denote the monoid of finite words and the set of infinite one-sided sequences with letters from
$\mathcal {A}^\infty $
to denote the monoid of finite words and the set of infinite one-sided sequences with letters from
![]() $\mathcal {A}$
, that is,
$\mathcal {A}$
, that is,
where
![]() $\epsilon $
is the unique empty word in
$\epsilon $
is the unique empty word in
![]() $\mathcal {A}^*$
. For a word
$\mathcal {A}^*$
. For a word
![]() $\mu \in A^*$
, we use
$\mu \in A^*$
, we use
![]() $|\mu |$
to denote the length of
$|\mu |$
to denote the length of
![]() $\mu $
and write
$\mu $
and write
![]() $|\mu |=n$
if
$|\mu |=n$
if
![]() $\mu \in \mathcal {A}^n$
. For the empty word, we usually define
$\mu \in \mathcal {A}^n$
. For the empty word, we usually define
![]() $|\epsilon |=0$
. In addition, the length of any element
$|\epsilon |=0$
. In addition, the length of any element
![]() $\mu $
in
$\mu $
in
![]() $\mathcal {A}^\infty $
is defined to be
$\mathcal {A}^\infty $
is defined to be
![]() $\infty $
. Let
$\infty $
. Let
![]() $\mu \in \mathcal {A}^*$
and
$\mu \in \mathcal {A}^*$
and
![]() $\nu \in \mathcal {A}^*\sqcup \mathcal {A}^\infty $
, and we say
$\nu \in \mathcal {A}^*\sqcup \mathcal {A}^\infty $
, and we say
![]() $\mu $
occurs in
$\mu $
occurs in
![]() $\nu $
, if there exists
$\nu $
, if there exists
![]() $a\in \mathcal {A}^*$
and
$a\in \mathcal {A}^*$
and
![]() $b\in \mathcal {A}^*\sqcup \mathcal {A}^\infty $
such that
$b\in \mathcal {A}^*\sqcup \mathcal {A}^\infty $
such that
If
![]() $\mu $
occurs in
$\mu $
occurs in
![]() $\nu $
, we also say
$\nu $
, we also say
![]() $\mu $
is a factor of
$\mu $
is a factor of
![]() $\nu $
.
$\nu $
.
A full shift is a continuous map
![]() $\sigma : x\mapsto \sigma (x)$
from
$\sigma : x\mapsto \sigma (x)$
from
![]() $\mathcal {A}^{\mathbb {N}}$
to
$\mathcal {A}^{\mathbb {N}}$
to
![]() $\mathcal {A}^{\mathbb {N}}$
(or
$\mathcal {A}^{\mathbb {N}}$
(or
![]() $\mathcal {A}^{\mathbb {Z}}$
to
$\mathcal {A}^{\mathbb {Z}}$
to
![]() $\mathcal {A}^{\mathbb {Z}}$
) such that
$\mathcal {A}^{\mathbb {Z}}$
) such that
A one-sided (two-sided, respectively) shift space is a nonempty compact
![]() $\sigma $
-invariant subspace X of
$\sigma $
-invariant subspace X of
![]() $\mathcal {A}^{\mathbb {N}}$
(or
$\mathcal {A}^{\mathbb {N}}$
(or
![]() $\mathcal {A}^{\mathbb {Z}}$
, respectively) together with the restriction
$\mathcal {A}^{\mathbb {Z}}$
, respectively) together with the restriction
![]() $\sigma |_X$
. Note that by
$\sigma |_X$
. Note that by
![]() $\sigma $
-invariant, we mean
$\sigma $
-invariant, we mean
![]() $\sigma (X)\subset X$
. Any two-sided shift is a homeomorphism, and any one-sided shift
$\sigma (X)\subset X$
. Any two-sided shift is a homeomorphism, and any one-sided shift
![]() $\sigma : X\to X$
is injective if and only if X is finite. Throughout the paper, we will only consider one-sided shifts on infinite compact spaces.
$\sigma : X\to X$
is injective if and only if X is finite. Throughout the paper, we will only consider one-sided shifts on infinite compact spaces.
If X is a shift space,
![]() $x\in X$
, and
$x\in X$
, and
![]() $-\infty <n\leq m<\infty $
, we define
$-\infty <n\leq m<\infty $
, we define
![]() $x_{(n-1,m]}=x_{[n,m+1)}=x_{[n,m]}=x_nx_{n+1}\cdots x_{m}$
. We also use
$x_{(n-1,m]}=x_{[n,m+1)}=x_{[n,m]}=x_nx_{n+1}\cdots x_{m}$
. We also use
![]() $x_{(-\infty , m]}=x_{(-\infty ,m+1)}$
or
$x_{(-\infty , m]}=x_{(-\infty ,m+1)}$
or
![]() $x_{[n,\infty )}=x_{(n-1,\infty )}$
to denote the natural infinite positive and negative parts of x, respectively.
$x_{[n,\infty )}=x_{(n-1,\infty )}$
to denote the natural infinite positive and negative parts of x, respectively.
For any two-sided shift space X, we use
![]() $X_+$
to stand for the corresponding one-sided shift space, that is,
$X_+$
to stand for the corresponding one-sided shift space, that is,
![]() $X_+=\{x_{[0,\infty )}: x\in X\}$
. If X is a one-sided shift space, then
$X_+=\{x_{[0,\infty )}: x\in X\}$
. If X is a one-sided shift space, then
![]() $\underline {X}$
is used, in this paper, to denote the inverse limit of the projective system
$\underline {X}$
is used, in this paper, to denote the inverse limit of the projective system
Note that
![]() $\underline {X}$
is a two-sided shift space under a canonical identification.
$\underline {X}$
is a two-sided shift space under a canonical identification.
For any shift space X, its language
![]() $\mathcal {L}(X)$
will play a central role, whose elements are those finite words over
$\mathcal {L}(X)$
will play a central role, whose elements are those finite words over
![]() $\mathcal {A}$
occurring in some
$\mathcal {A}$
occurring in some
![]() $x\in X$
. A language uniquely determines a shift space, or in other words,
$x\in X$
. A language uniquely determines a shift space, or in other words,
![]() $x\in X$
if and only if any factor
$x\in X$
if and only if any factor
![]() $\mu $
of x is an element of
$\mu $
of x is an element of
![]() $\mathcal {L}(X)$
. This fact implies that for any two-sided shift space Y,
$\mathcal {L}(X)$
. This fact implies that for any two-sided shift space Y,
![]() $\sigma (Y)=Y$
, and therefore for any one-sided shift space X,
$\sigma (Y)=Y$
, and therefore for any one-sided shift space X,
![]() $\sigma (X)=X$
if and only if
$\sigma (X)=X$
if and only if
![]() $X=(\underline {X})_+$
. Any topologically transitive one-sided shift (for the definition of topologically transitivity, see Proposition 3.10) is automatically surjective since its image is a dense compact subset.
$X=(\underline {X})_+$
. Any topologically transitive one-sided shift (for the definition of topologically transitivity, see Proposition 3.10) is automatically surjective since its image is a dense compact subset.
Definition 2.1 Let X be a one-sided shift space, and let
![]() $x\in X$
. We define the forward and backward orbits of x to be
$x\in X$
. We define the forward and backward orbits of x to be
respectively, and the whole orbit of x to be
![]() $\mathrm{Orb}_\sigma (x)=\mathrm{Orb}^+_{\sigma }(x)\cup \mathrm{Orb}^-_{\sigma }(x)$
.
$\mathrm{Orb}_\sigma (x)=\mathrm{Orb}^+_{\sigma }(x)\cup \mathrm{Orb}^-_{\sigma }(x)$
.
2.2
 $C^*$
-algebras and groupoids
$C^*$
-algebras and groupoids
Definition 2.2 (Cf. [Reference Williams21, Definition 2.1])
Let A and B be
![]() $C^*$
-algebras. A
$C^*$
-algebras. A
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi : A\to B$
is said to have nuclear dimension at most n, denoted
$\pi : A\to B$
is said to have nuclear dimension at most n, denoted
![]() $\mathrm {dim}_{\mathrm {nuc}}(\pi )\leq n$
, if for any finite set
$\mathrm {dim}_{\mathrm {nuc}}(\pi )\leq n$
, if for any finite set
![]() ${\mathcal F}\subset A$
and
${\mathcal F}\subset A$
and
![]() $\varepsilon>0$
, there is a finite-dimensional subalgebra F and completely positive maps
$\varepsilon>0$
, there is a finite-dimensional subalgebra F and completely positive maps
![]() $\psi : A\to F$
and
$\psi : A\to F$
and
![]() $\varphi : F\to B$
such that
$\varphi : F\to B$
such that
![]() $\psi $
is contractive,
$\psi $
is contractive,
![]() $\varphi $
is n-decomposable in the sense that we can write
$\varphi $
is n-decomposable in the sense that we can write
satisfying
![]() $\varphi |_{F^{(i)}}$
is completely positive contractive and order zero for all i, and for every
$\varphi |_{F^{(i)}}$
is completely positive contractive and order zero for all i, and for every
![]() $a\in {\mathcal F}$
,
$a\in {\mathcal F}$
,
The nuclear dimension of a
![]() $C^*$
-algebra A, denoted
$C^*$
-algebra A, denoted
![]() $\mathrm {dim}_{\mathrm {nuc}}(A)$
, is defined as the nuclear dimension of the identity homomorphism
$\mathrm {dim}_{\mathrm {nuc}}(A)$
, is defined as the nuclear dimension of the identity homomorphism
![]() $\mathrm {id}_A$
.
$\mathrm {id}_A$
.
We now recall the definitions of groupoid and its dynamic asymptotic dimension.
Definition 2.3 (Cf. [Reference Sims and Williams20, equation (3.1)])
Let X be a local homeomorphism on a compact Hausdorff space X. We then obtain a dynamical system
![]() $(X, T)$
. The corresponding Deaconu–Renault Groupoid is defined to be the set
$(X, T)$
. The corresponding Deaconu–Renault Groupoid is defined to be the set
with the unit space
![]() $\mathcal {G}_{X}^0=\{(x,0,x): x\in X\}$
identified with X, range and source maps
$\mathcal {G}_{X}^0=\{(x,0,x): x\in X\}$
identified with X, range and source maps
![]() $r(x,n,y)=x$
and
$r(x,n,y)=x$
and
![]() $s(x,n,y)=y$
, and operations
$s(x,n,y)=y$
, and operations
![]() $(x,n,y)(y,m,z)=(x,n+m,z)$
and
$(x,n,y)(y,m,z)=(x,n+m,z)$
and
![]() $(x,n,y)^{-1}=(y,-n,x)$
.
$(x,n,y)^{-1}=(y,-n,x)$
.
By Lemma 2.3 in [Reference Brix and Carlsen4] and Lemmas 3.1 and 3.5 in [Reference Sims and Williams20], the groupoids
![]() $\mathcal {G}_{\widetilde {X}}$
considered in the paper will all be locally compact, Hausdorff, amenable, and étale, where
$\mathcal {G}_{\widetilde {X}}$
considered in the paper will all be locally compact, Hausdorff, amenable, and étale, where
![]() $\widetilde {X}$
is the cover of X in the sense of Definition 3.19. They are also principal since all such
$\widetilde {X}$
is the cover of X in the sense of Definition 3.19. They are also principal since all such
![]() $\widetilde {X}$
have no periodic point, as is shown in Section 4.
$\widetilde {X}$
have no periodic point, as is shown in Section 4.
The Cuntz–Pimsner
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_X$
of a one-sided shift space X is defined to be the (full) groupoid
$\mathcal {O}_X$
of a one-sided shift space X is defined to be the (full) groupoid
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(\mathcal {G}_{\widetilde {X}})$
. The diagonal subalgebra
$C^*(\mathcal {G}_{\widetilde {X}})$
. The diagonal subalgebra
![]() $\mathcal {D}_X$
is defined to be
$\mathcal {D}_X$
is defined to be
![]() $C(\widetilde {X})\subset \mathcal {O}_X$
.
$C(\widetilde {X})\subset \mathcal {O}_X$
.
Finally, we recall the definition of dynamic asymptotic dimension for étale groupoids.
Definition 2.4 (Cf. [Reference Guentner, Willett and Yu12, Definition 5.1])
Let
![]() $\mathcal {G}$
be an étale groupoid. Then
$\mathcal {G}$
be an étale groupoid. Then
![]() $\mathcal {G}$
has dynamic asymptotic dimension
$\mathcal {G}$
has dynamic asymptotic dimension
![]() $d\in \mathbb {N}$
if d is the smallest number with the following property: for every open relatively compact subset K of
$d\in \mathbb {N}$
if d is the smallest number with the following property: for every open relatively compact subset K of
![]() $\mathcal {G}$
, there are open subsets
$\mathcal {G}$
, there are open subsets
![]() $U_0, U_1,\ldots ,U_d$
of
$U_0, U_1,\ldots ,U_d$
of
![]() $\mathcal {G}^0$
that covers
$\mathcal {G}^0$
that covers
![]() $s(K)\cup r(K)$
such that for each i, the set
$s(K)\cup r(K)$
such that for each i, the set
![]() $\{g\in K: s(g),r(g)\in U_i\}$
is contained in a relatively compact subgroupoid of
$\{g\in K: s(g),r(g)\in U_i\}$
is contained in a relatively compact subgroupoid of
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
It is known that for a minimal
![]() $\mathbb {Z}$
-action on a compact space, the associated groupoid has dynamic asymptotic dimension
$\mathbb {Z}$
-action on a compact space, the associated groupoid has dynamic asymptotic dimension
![]() $1$
(see Theorem 3.1 in [Reference Guentner, Willett and Yu12]).
$1$
(see Theorem 3.1 in [Reference Guentner, Willett and Yu12]).
3 Definitions and preparations
From now on, to avoid invalidity or triviality, we only consider infinite one-sided shift space X with
![]() $\sigma (X)=X$
. We use
$\sigma (X)=X$
. We use
![]() $\underline {X}$
to denote the associated two-sided shift space.
$\underline {X}$
to denote the associated two-sided shift space.
3.1 Left special elements and past equivalence
Definition 3.1 (Cf. [Reference Carlsen and Eilers8, subsection 2.2, the first paragraph])
Let X be a one-sided shift space and
![]() $z\in \underline {X}$
. We say that z is left special if there exists
$z\in \underline {X}$
. We say that z is left special if there exists
![]() $z'\in \underline {X}$
such that
$z'\in \underline {X}$
such that
![]() $z_{-1}\neq z^{\prime }_{-1}$
and
$z_{-1}\neq z^{\prime }_{-1}$
and
![]() $z_{[0,\infty )}=z^{\prime }_{[0,\infty )}$
. If
$z_{[0,\infty )}=z^{\prime }_{[0,\infty )}$
. If
![]() $z\in \underline {X}$
is left special, we also say
$z\in \underline {X}$
is left special, we also say
![]() $x=z_{[0,\infty )}$
is left special in X. We use
$x=z_{[0,\infty )}$
is left special in X. We use
![]() $\mathrm{Sp}_\mathrm{l}(\underline {X})$
and
$\mathrm{Sp}_\mathrm{l}(\underline {X})$
and
![]() $\mathrm{Sp}_\mathrm{l}(X)$
to denote the collections of left special elements in
$\mathrm{Sp}_\mathrm{l}(X)$
to denote the collections of left special elements in
![]() $\underline {X}$
and X, respectively.
$\underline {X}$
and X, respectively.
We say
![]() $x\in X$
has a unique past if
$x\in X$
has a unique past if
![]() $\#(\sigma ^{k})^{-1}(\{x\})=1$
for all
$\#(\sigma ^{k})^{-1}(\{x\})=1$
for all
![]() $k\geq 1$
. Moreover, we say
$k\geq 1$
. Moreover, we say
![]() $x\in X$
has a totally unique past if
$x\in X$
has a totally unique past if
![]() $\sigma ^n(x)$
has a unique past for all
$\sigma ^n(x)$
has a unique past for all
![]() $n\geq 1$
.
$n\geq 1$
.
It is clear from the definition that for any one-sided shift space X with
![]() $\sigma (X)=X$
, a point
$\sigma (X)=X$
, a point
![]() $x\in X$
is left special precisely when x has at least two preimages under
$x\in X$
is left special precisely when x has at least two preimages under
![]() $\sigma $
, that is,
$\sigma $
, that is,
![]() $\#\sigma ^{-1}(\{x\})\ge 2$
. Therefore, for any such one-sided shift on an infinite space, left special element always exists, or
$\#\sigma ^{-1}(\{x\})\ge 2$
. Therefore, for any such one-sided shift on an infinite space, left special element always exists, or
![]() $\sigma $
will be injective, which implies that X is finite. It is also immediate that x has a totally unique past if and only if
$\sigma $
will be injective, which implies that X is finite. It is also immediate that x has a totally unique past if and only if
![]() $x\notin \mathrm{Orb}_\sigma (\omega )$
for any
$x\notin \mathrm{Orb}_\sigma (\omega )$
for any
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
.
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
.
Proposition 3.2 Suppose that
![]() $\mathrm{Sp}_\mathrm{l}(X)$
contains no periodic point of X. Then
$\mathrm{Sp}_\mathrm{l}(X)$
contains no periodic point of X. Then
![]() ${\#\mathrm{Sp}_\mathrm{l}(\underline {X})<\infty }$
if and only if
${\#\mathrm{Sp}_\mathrm{l}(\underline {X})<\infty }$
if and only if
![]() $\#\mathrm{Sp}_\mathrm{l}(X)<\infty $
.
$\#\mathrm{Sp}_\mathrm{l}(X)<\infty $
.
Proof The map
![]() $\pi _+: z\mapsto z_{[0,\infty )}$
induces a surjective map from
$\pi _+: z\mapsto z_{[0,\infty )}$
induces a surjective map from
![]() $\mathrm{Sp}_\mathrm{l}(\underline {X})$
to
$\mathrm{Sp}_\mathrm{l}(\underline {X})$
to
![]() $\mathrm{Sp}_\mathrm{l}(X)$
. Therefore, if
$\mathrm{Sp}_\mathrm{l}(X)$
. Therefore, if
![]() $\mathrm{Sp}_\mathrm{l}(\underline {X})$
is finite, so is
$\mathrm{Sp}_\mathrm{l}(\underline {X})$
is finite, so is
![]() $\mathrm{Sp}_\mathrm{l}(X)$
.
$\mathrm{Sp}_\mathrm{l}(X)$
.
Now assume that
![]() $\mathrm{Sp}(\underline {X})$
is infinite. If
$\mathrm{Sp}(\underline {X})$
is infinite. If
![]() $\mathrm{Sp}(X)$
is finite, then we can take
$\mathrm{Sp}(X)$
is finite, then we can take
![]() $x\in \mathrm{Sp}_\mathrm{l}(X)$
with infinitely many preimages in
$x\in \mathrm{Sp}_\mathrm{l}(X)$
with infinitely many preimages in
![]() $\mathrm{Sp}_\mathrm{l}(\underline {X})$
under
$\mathrm{Sp}_\mathrm{l}(\underline {X})$
under
![]() $\pi _+$
. Denote this infinite preimage by
$\pi _+$
. Denote this infinite preimage by
![]() $F$
. Since
$F$
. Since
![]() $\mathcal {A}$
is finite, the Pigeonhole principle ensures the existence of an infinite subset
$\mathcal {A}$
is finite, the Pigeonhole principle ensures the existence of an infinite subset
![]() $F_1\subset F$
such that for every
$F_1\subset F$
such that for every
![]() $x\neq y\in F_1$
,
$x\neq y\in F_1$
,
![]() $x_{[-1,\infty )}=y_{[-1,\infty )}$
. Then we choose
$x_{[-1,\infty )}=y_{[-1,\infty )}$
. Then we choose
![]() $n_1\leq -1$
such that there exists
$n_1\leq -1$
such that there exists
![]() $x^1,y^1\in F_1$
with
$x^1,y^1\in F_1$
with
This means that there is some
![]() $z^1\in F_1$
such that
$z^1\in F_1$
such that
![]() $(z^1)_{[n_1,\infty )}\in \mathrm{Sp}_\mathrm{l}(X)$
. Similarly, choose an infinite subset
$(z^1)_{[n_1,\infty )}\in \mathrm{Sp}_\mathrm{l}(X)$
. Similarly, choose an infinite subset
![]() $F_2\subset F_1$
, an integer
$F_2\subset F_1$
, an integer
![]() $n_2\leq n_1-1$
with the same property as the first step, and a point
$n_2\leq n_1-1$
with the same property as the first step, and a point
![]() $z^2\in F_2$
such that
$z^2\in F_2$
such that
![]() $(z^2)_{[n_2,\infty )}\in \mathrm{Sp}_\mathrm{l}(X)$
. Repeating this procedure, we have a strictly decreasing sequence of negative integers
$(z^2)_{[n_2,\infty )}\in \mathrm{Sp}_\mathrm{l}(X)$
. Repeating this procedure, we have a strictly decreasing sequence of negative integers
![]() $\{n_k\}_{k\geq 1}$
and an infinite sequence
$\{n_k\}_{k\geq 1}$
and an infinite sequence
![]() $\{z^k\}_{k\geq 1}\subset \mathrm{Sp}_\mathrm{l}(\underline {X})$
with the following property:
$\{z^k\}_{k\geq 1}\subset \mathrm{Sp}_\mathrm{l}(\underline {X})$
with the following property:
Note that it follows from the latter condition that
![]() $(z^k)_{[n_k,\infty )}$
all lie on a single orbit in X. Since
$(z^k)_{[n_k,\infty )}$
all lie on a single orbit in X. Since
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite, it has to contain a periodic point, which is a contradiction.
$\mathrm{Sp}_\mathrm{l}(X)$
is finite, it has to contain a periodic point, which is a contradiction.
Notation. Let
![]() $S\subset X$
be a set, and let
$S\subset X$
be a set, and let
![]() $l\in \mathbb {N}$
. We define
$l\in \mathbb {N}$
. We define
![]() $S_{[0,l]}$
to be the set whose elements are the prefixes of
$S_{[0,l]}$
to be the set whose elements are the prefixes of
![]() $x\in S$
of length
$x\in S$
of length
![]() $l+1$
.
$l+1$
.
Definition 3.3 (Cf. [Reference Carlsen and Eilers8, subsection 2.4, the first paragraph])
Let X be a one-sided shift space, and let
![]() $l\geq 1$
. For
$l\geq 1$
. For
![]() $x\in X$
, set
$x\in X$
, set
For
![]() $x,y\in X$
, we say x and y are l-past equivalent and write
$x,y\in X$
, we say x and y are l-past equivalent and write
![]() $x\sim _l y$
, if
$x\sim _l y$
, if
![]() $P_l(x)=P_l(y)$
. In particular, x and y are said to be past equivalent if
$P_l(x)=P_l(y)$
. In particular, x and y are said to be past equivalent if
![]() $x\sim _ly$
for some
$x\sim _ly$
for some
![]() $l\geq 1$
.
$l\geq 1$
.
We call x isolated in past equivalent if there exists
![]() $l\geq 1$
such that
$l\geq 1$
such that
![]() $x\sim _ly$
implies
$x\sim _ly$
implies
![]() $x=y$
.
$x=y$
.
If
![]() $x\sim _{l+1}y$
, then
$x\sim _{l+1}y$
, then
![]() $x\sim _ky$
for all
$x\sim _ky$
for all
![]() $1\leq k\leq l$
. Consequently, if x is isolated in l-past equivalent, then x is isolated in k-past equivalent for every
$1\leq k\leq l$
. Consequently, if x is isolated in l-past equivalent, then x is isolated in k-past equivalent for every
![]() $k\geq l$
.
$k\geq l$
.
Lemma 3.4 Suppose that
![]() $x\in X$
has a unique past. Then, for every
$x\in X$
has a unique past. Then, for every
![]() $l\geq 1$
, there exists
$l\geq 1$
, there exists
![]() $N\in \mathbb {N}$
such that, whenever
$N\in \mathbb {N}$
such that, whenever
![]() $y\in X$
with
$y\in X$
with
![]() $y_{[0,N]}=x_{[0,N]}$
,
$y_{[0,N]}=x_{[0,N]}$
,
![]() $\#P_l(y)=1$
.
$\#P_l(y)=1$
.
Proof Assume that there exists
![]() $l_0\geq 1$
such that for every
$l_0\geq 1$
such that for every
![]() $n\in \mathbb {N}$
, we can always find some
$n\in \mathbb {N}$
, we can always find some
![]() $y^n\in X$
with
$y^n\in X$
with
![]() $y^n_{[0,n]}=x_{[0,n]}$
, but
$y^n_{[0,n]}=x_{[0,n]}$
, but
![]() $\#P_{l_0}(y^n)\ge 2$
. We are then given a sequence
$\#P_{l_0}(y^n)\ge 2$
. We are then given a sequence
![]() $\{y^n\}_{n\geq 0}$
which is easily seen to converge to x as
$\{y^n\}_{n\geq 0}$
which is easily seen to converge to x as
![]() $n\to \infty $
.
$n\to \infty $
.
Note that the alphabet
![]() $\mathcal {A}$
is finite, we now claim that there exist two distinct words
$\mathcal {A}$
is finite, we now claim that there exist two distinct words
![]() $\mu ,\nu $
in
$\mu ,\nu $
in
![]() $\mathcal {L}(X)$
of length
$\mathcal {L}(X)$
of length
![]() $l_0$
such that two sequences of natural numbers
$l_0$
such that two sequences of natural numbers
![]() $\{n_k\}_{k\ge 0}$
and
$\{n_k\}_{k\ge 0}$
and
![]() $\{m_k\}_{k\ge 0}$
can be chosen, satisfying
$\{m_k\}_{k\ge 0}$
can be chosen, satisfying
In fact, from the Pigeonhole principle, there is at least one word
![]() $\mu $
with
$\mu $
with
![]() $|\mu |=l_0$
such that
$|\mu |=l_0$
such that
![]() $\mu $
can be a prefix of infinitely many
$\mu $
can be a prefix of infinitely many
![]() $y^n$
, say,
$y^n$
, say,
![]() $y^{n_k}$
for
$y^{n_k}$
for
![]() $k\geq 1$
. However, if
$k\geq 1$
. However, if
![]() $\mu $
is the unique word with such property, then all others in
$\mu $
is the unique word with such property, then all others in
![]() $\mathcal {L}(X)$
with length
$\mathcal {L}(X)$
with length
![]() $l_0$
can only be prefixes of finitely many of
$l_0$
can only be prefixes of finitely many of
![]() $y^n$
, and which means that for some natural number N,
$y^n$
, and which means that for some natural number N,
![]() $y^n$
will only have the unique prefix
$y^n$
will only have the unique prefix
![]() $\mu $
whenever
$\mu $
whenever
![]() $n\geq N$
. This is then a contradiction.
$n\geq N$
. This is then a contradiction.
Finally, note that since
![]() $y^n\to x$
as
$y^n\to x$
as
![]() $n\to \infty $
, every finite word occurring in
$n\to \infty $
, every finite word occurring in
![]() $\mu x$
and
$\mu x$
and
![]() $\nu x$
is an element of
$\nu x$
is an element of
![]() $\mathcal {L}(X)$
. This proves
$\mathcal {L}(X)$
. This proves
![]() $\mu x, \nu x\in X$
, and hence x does not have a unique past.
$\mu x, \nu x\in X$
, and hence x does not have a unique past.
3.2 Right tail equivalence and
 $\mathfrak {j}$
-maximal elements
$\mathfrak {j}$
-maximal elements
Definition 3.5 (Cf. [Reference Carlsen and Eilers8, subsection 2.2, the last paragraph] [a slightly different version)]
Let
![]() $x,x'\in X$
. The notation
$x,x'\in X$
. The notation
![]() $x\sim _{\mathrm{rte}}x'$
is used to mean that x and
$x\sim _{\mathrm{rte}}x'$
is used to mean that x and
![]() $x'$
are right tail equivalent, in the sense that there exist
$x'$
are right tail equivalent, in the sense that there exist
![]() $M, M'\in \mathbb {N}$
satisfying
$M, M'\in \mathbb {N}$
satisfying
Set
![]() $\mathcal {J}_X=\mathrm{Sp}_\mathrm{l}(X)/\sim _{\mathrm{rte}}$
. Let
$\mathcal {J}_X=\mathrm{Sp}_\mathrm{l}(X)/\sim _{\mathrm{rte}}$
. Let
![]() $\mathfrak {j}\in \mathcal {J}_X$
and
$\mathfrak {j}\in \mathcal {J}_X$
and
![]() $\omega \in \mathfrak {j}$
. We say
$\omega \in \mathfrak {j}$
. We say
![]() $\omega $
is
$\omega $
is
![]() $\mathfrak {j}$
-maximal if, for any
$\mathfrak {j}$
-maximal if, for any
![]() $\omega '\in \mathfrak {j}$
, there is an
$\omega '\in \mathfrak {j}$
, there is an
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $\sigma ^m(\omega ')=\omega $
.
$\sigma ^m(\omega ')=\omega $
.
Proposition 3.6 Suppose that
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point of X. Then every
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point of X. Then every
![]() $\mathfrak {j}\in \mathcal {J}_X$
has a unique
$\mathfrak {j}\in \mathcal {J}_X$
has a unique
![]() $\mathfrak {j}$
-maximal element. In particular, an element
$\mathfrak {j}$
-maximal element. In particular, an element
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
is
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
is
![]() $\mathfrak {j}$
-maximal if and only if
$\mathfrak {j}$
-maximal if and only if
Proof Let
![]() $\eta \in \mathfrak {j}$
be arbitrary. Since
$\eta \in \mathfrak {j}$
be arbitrary. Since
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point, we can take
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point, we can take
![]() $K\in \mathbb {N}$
such that
$K\in \mathbb {N}$
such that
![]() $\sigma ^K(\eta )\in \mathrm{Sp}_\mathrm{l}(X)$
, but
$\sigma ^K(\eta )\in \mathrm{Sp}_\mathrm{l}(X)$
, but
![]() $\sigma ^k(\eta )\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
$\sigma ^k(\eta )\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
![]() $k\geq K+1$
. Denote
$k\geq K+1$
. Denote
![]() $\sigma ^K(\eta )$
by
$\sigma ^K(\eta )$
by
![]() $\omega $
. We prove the proposition by showing that
$\omega $
. We prove the proposition by showing that
![]() $\omega $
is
$\omega $
is
![]() $\mathfrak {j}$
-maximal.
$\mathfrak {j}$
-maximal.
Let
![]() $\omega '\in \mathfrak {j}\setminus \{\omega \}$
. Since
$\omega '\in \mathfrak {j}\setminus \{\omega \}$
. Since
![]() $\omega \sim _{\mathrm{rte}}\omega '$
, there are
$\omega \sim _{\mathrm{rte}}\omega '$
, there are
![]() $M,M'\in \mathbb {N}$
such that
$M,M'\in \mathbb {N}$
such that
Take the minimal nonnegative integer M so that there is
![]() $M'\in \mathbb {N}$
with
$M'\in \mathbb {N}$
with
![]() $\sigma ^M(\omega )=\sigma ^{M'}(\omega ')$
. If
$\sigma ^M(\omega )=\sigma ^{M'}(\omega ')$
. If
![]() $M>0$
, then
$M>0$
, then
![]() $\omega _{M-1}\neq w^{\prime }_{M'-1}$
, which means that
$\omega _{M-1}\neq w^{\prime }_{M'-1}$
, which means that
![]() $\omega _{[M,\infty )}=\omega ^{\prime }_{[M',\infty )}$
is left special. Note that
$\omega _{[M,\infty )}=\omega ^{\prime }_{[M',\infty )}$
is left special. Note that
![]() $\omega _{[M,\infty )}=\sigma ^{k+M}(\eta )$
. However, this contradicts to the assumption that
$\omega _{[M,\infty )}=\sigma ^{k+M}(\eta )$
. However, this contradicts to the assumption that
![]() $\sigma ^k(\eta )\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
$\sigma ^k(\eta )\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
![]() $k\geq K+1$
. Consequently,
$k\geq K+1$
. Consequently,
![]() $M=0$
; in other words,
$M=0$
; in other words,
![]() $\omega =\sigma ^{M'-1}(\omega ')$
. This proves the existence of
$\omega =\sigma ^{M'-1}(\omega ')$
. This proves the existence of
![]() $\mathfrak {j}$
-maximal elements.
$\mathfrak {j}$
-maximal elements.
The uniqueness follows directly from the absence of periodic point in
![]() $\mathrm{Sp}_\mathrm{l}(X)$
. Finally, the above argument verifies the second assertion at the same time.
$\mathrm{Sp}_\mathrm{l}(X)$
. Finally, the above argument verifies the second assertion at the same time.
Definition 3.7 Let X be a one-sided shift space with finite left special elements. From now on, for any
![]() $\mathfrak {j}\in \mathcal {J}_X$
, we will always denote the unique
$\mathfrak {j}\in \mathcal {J}_X$
, we will always denote the unique
![]() $\mathfrak {j}$
-maximal element by
$\mathfrak {j}$
-maximal element by
![]() $\omega _{\mathfrak {j}}$
. For every
$\omega _{\mathfrak {j}}$
. For every
![]() $\mathfrak {j}\in \mathcal {J}_X$
, define
$\mathfrak {j}\in \mathcal {J}_X$
, define
Note that for all
![]() $\omega \in U_{\mathfrak {j}}$
,
$\omega \in U_{\mathfrak {j}}$
,
![]() ${\alpha }\omega $
has a unique past whenever
${\alpha }\omega $
has a unique past whenever
![]() ${\alpha }\omega \in X$
for some
${\alpha }\omega \in X$
for some
![]() ${\alpha }\in \mathcal {A}$
.
${\alpha }\in \mathcal {A}$
.
Lemma 3.8 Suppose
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point. For every
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point. For every
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
, there is
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
, there is
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\sigma ^n(\omega )$
is isolated in l-past equivalence for all
$\sigma ^n(\omega )$
is isolated in l-past equivalence for all
![]() $l>n\geq N$
.
$l>n\geq N$
.
Proof Let
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
. From Proposition 3.6, let
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
. From Proposition 3.6, let
![]() $m\in \mathbb {N}$
be such that
$m\in \mathbb {N}$
be such that
![]() $w_{\mathfrak {j}}=\sigma ^m(\omega )$
is
$w_{\mathfrak {j}}=\sigma ^m(\omega )$
is
![]() $\mathfrak {j}$
-maximal for some
$\mathfrak {j}$
-maximal for some
![]() $\mathfrak {j}\in \mathcal {J}_X$
. Since
$\mathfrak {j}\in \mathcal {J}_X$
. Since
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite, there exists
$\mathrm{Sp}_\mathrm{l}(X)$
is finite, there exists
![]() $N'\in \mathbb {N}$
with the following property:
$N'\in \mathbb {N}$
with the following property:
Let
![]() $N=N'+m$
. Then
$N=N'+m$
. Then
![]() $\sigma ^N(\omega )$
is isolated in
$\sigma ^N(\omega )$
is isolated in
![]() $N'+1$
-past equivalence, and therefore for every
$N'+1$
-past equivalence, and therefore for every
![]() $l>n\geq N$
,
$l>n\geq N$
,
![]() $\sigma ^n(\omega )$
is isolated in l-past equivalence as well.
$\sigma ^n(\omega )$
is isolated in l-past equivalence as well.
3.3 Properties (*) and (**)
Definition 3.9 (Cf. [Reference Carlsen and Eilers8, Definition 3.1])
A one-sided shift space X has property (*) if for every
![]() $\mu \in \mathcal {L}(X)$
, there exists
$\mu \in \mathcal {L}(X)$
, there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $P_{|\mu |}(x)=\{\mu \}$
. We will also say
$P_{|\mu |}(x)=\{\mu \}$
. We will also say
![]() $\underline {X}$
has property (*) if X does so.
$\underline {X}$
has property (*) if X does so.
Proposition 3.10 Let X be a one-sided shift space. Suppose that X is topologically transitive, namely, there is a point
![]() $x^0\in X$
such that its forward orbit is dense in X. If
$x^0\in X$
such that its forward orbit is dense in X. If
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point in X, then X has property (*).
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point in X, then X has property (*).
Actually, the proof is basically the same as that of Example 3.6 in [Reference Carlsen and Eilers8] for the minimal case, which goes like follows. Since X is transitive, take
![]() $x^0\in X$
with a dense forward orbit, which follows that every word in
$x^0\in X$
with a dense forward orbit, which follows that every word in
![]() $\mathcal {L}(X)$
occurs in
$\mathcal {L}(X)$
occurs in
![]() $x^0$
. Therefore, it suffices to show that, for every word
$x^0$
. Therefore, it suffices to show that, for every word
![]() $\mu $
occurring in
$\mu $
occurring in
![]() $x^0$
, there exists
$x^0$
, there exists
![]() $y^0$
such that
$y^0$
such that
![]() $P_{|\mu |}(y^0)=\{\mu \}$
. Now, since
$P_{|\mu |}(y^0)=\{\mu \}$
. Now, since
![]() $x^0$
is a transitive point,
$x^0$
is a transitive point,
![]() $\mu $
appears in
$\mu $
appears in
![]() $x^0$
infinitely many times. Consider the intersection
$x^0$
infinitely many times. Consider the intersection
Since
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point, this intersection has to be finite, which means that there exists
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point, this intersection has to be finite, which means that there exists
![]() $N\geq 1$
such that
$N\geq 1$
such that
![]() $\sigma ^{n}(x^0)\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
$\sigma ^{n}(x^0)\notin \mathrm{Sp}_\mathrm{l}(X)$
for all
![]() $n\geq N$
. This follows that for all
$n\geq N$
. This follows that for all
![]() $n\geq N$
,
$n\geq N$
,
![]() $\sigma ^n(x^0)$
has only one preimage. Upon taking
$\sigma ^n(x^0)$
has only one preimage. Upon taking
![]() $L>N+|\mu |$
with
$L>N+|\mu |$
with
![]() $(x^0)_{[L-|\mu |+1,L]}=\mu $
, we conclude that
$(x^0)_{[L-|\mu |+1,L]}=\mu $
, we conclude that
![]() $\sigma ^{L+1}(x^0)$
has only one preimage of length
$\sigma ^{L+1}(x^0)$
has only one preimage of length
![]() $|\mu |$
, and which is exactly
$|\mu |$
, and which is exactly
![]() $\mu $
.
$\mu $
.
Definition 3.11 (Cf. [Reference Carlsen and Eilers8, Definition 3.2])
Let X be a one-sided shift space with property (*). If, in addition,
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point in X, then we say X has property (**).
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point in X, then we say X has property (**).
Proposition 3.10 together with Proposition 3.2 implies the following corollary.
Corollary 3.12 A transitive one-sided shift space X has property (**) if and only if
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point. In particular, if X is minimal, then X has property (**) exactly when
$\mathrm{Sp}_\mathrm{l}(X)$
is finite and contains no periodic point. In particular, if X is minimal, then X has property (**) exactly when
![]() $\mathrm{Sp}_\mathrm{l}(X)$
is finite.
$\mathrm{Sp}_\mathrm{l}(X)$
is finite.
Example 3.13 Every nonregular Toeplitz shifts has property (*), as is shown in [Reference Carlsen and Eilers8].
We now prove that this is the case for every nonperiodic Toeplitz shift. The same notations as in [Reference Winter and Zacharias22] will be used in the following proposition.
Proposition 3.14 Let
![]() $\eta $
be a nonperiodic Toeplitz sequence. Then
$\eta $
be a nonperiodic Toeplitz sequence. Then
![]() $X_\eta $
has property (*).
$X_\eta $
has property (*).
Proof Let
![]() $\mu \in \mathcal {L}(X_\eta )$
. Without loss of generality, assume that
$\mu \in \mathcal {L}(X_\eta )$
. Without loss of generality, assume that
![]() $\eta _{[0, m-1]}=\mu $
for
$\eta _{[0, m-1]}=\mu $
for
![]() $m=|\mu |$
. We show that
$m=|\mu |$
. We show that
Suppose
![]() $\mu '\in \mathcal {L}(X_\eta )$
with
$\mu '\in \mathcal {L}(X_\eta )$
with
![]() $\mu '\eta _{[m,\infty )}\in X_\eta $
. Then
$\mu '\eta _{[m,\infty )}\in X_\eta $
. Then
![]() $\mu '\eta _{[m,\infty )}$
can be approximated by a sequence
$\mu '\eta _{[m,\infty )}$
can be approximated by a sequence
![]() $\sigma ^{n_k}(\eta )$
. Write
$\sigma ^{n_k}(\eta )$
. Write
![]() $\mu =\mu _1\mu _2\ldots \mu _{|\mu |}$
. We then note that
$\mu =\mu _1\mu _2\ldots \mu _{|\mu |}$
. We then note that
![]() $\eta _{m-1}=\mu _{|\mu |}$
.
$\eta _{m-1}=\mu _{|\mu |}$
.
Consider the
![]() $p_{m-1}$
-skeleton of
$p_{m-1}$
-skeleton of
![]() $\eta $
, say,
$\eta $
, say,
![]() $\tilde {\eta }\in (\mathcal {A}\cup \{\infty \})^{\mathbb {N}}$
. Then
$\tilde {\eta }\in (\mathcal {A}\cup \{\infty \})^{\mathbb {N}}$
. Then
![]() $\tilde {\eta }$
is a periodic sequence with period orbit
$\tilde {\eta }$
is a periodic sequence with period orbit
![]() $\{\tilde {\eta }, \sigma (\tilde {\eta }), \ldots , \sigma ^{p_{m-1}-1}(\tilde {\eta })\}$
. From the Pigeonhole principle, there is
$\{\tilde {\eta }, \sigma (\tilde {\eta }), \ldots , \sigma ^{p_{m-1}-1}(\tilde {\eta })\}$
. From the Pigeonhole principle, there is
![]() $0\leq l\leq p_{m-1}-1$
such that there exist infinitely many
$0\leq l\leq p_{m-1}-1$
such that there exist infinitely many
![]() $n_{k_j}\,(j=1,2,\ldots )$
satisfying
$n_{k_j}\,(j=1,2,\ldots )$
satisfying
for some
![]() $l\in \{0,1,\ldots ,p_{m-1}-1\}$
, which follows
$l\in \{0,1,\ldots ,p_{m-1}-1\}$
, which follows
![]() $(\sigma ^{n_{k_j}}(\eta ))_n=\eta _{m-1}$
for all
$(\sigma ^{n_{k_j}}(\eta ))_n=\eta _{m-1}$
for all
![]() $n\in (l+m-1)+p_{m-1}\mathbb {N}$
, and therefore
$n\in (l+m-1)+p_{m-1}\mathbb {N}$
, and therefore
for all
![]() $n\in (l+m-1)+p_{m-1}\mathbb {N}$
. Due to the fact that the p-skeleton of a given Toeplitz sequence is the “maximal” periodic part with the given period,
$n\in (l+m-1)+p_{m-1}\mathbb {N}$
. Due to the fact that the p-skeleton of a given Toeplitz sequence is the “maximal” periodic part with the given period,
![]() $\tilde {\eta }$
plays the central role. Hence, the assumption that
$\tilde {\eta }$
plays the central role. Hence, the assumption that
![]() $\mu '\eta _{[m,\infty )}$
and
$\mu '\eta _{[m,\infty )}$
and
![]() $\mu \eta _{[m,\infty )}$
have a common right infinite section yields that
$\mu \eta _{[m,\infty )}$
have a common right infinite section yields that
![]() $l=0$
. We then conclude that for all
$l=0$
. We then conclude that for all
![]() $n\in m-1+p_{m-1}\mathbb {N}$
,
$n\in m-1+p_{m-1}\mathbb {N}$
,
and, in particular,
![]() $\mu ^{\prime }_{m}=\mu _m$
. By repeatedly applying this procedure to
$\mu ^{\prime }_{m}=\mu _m$
. By repeatedly applying this procedure to
![]() $m-1, m-2,\ldots ,0$
, we therefore have
$m-1, m-2,\ldots ,0$
, we therefore have
![]() $\mu '=\mu $
.
$\mu '=\mu $
.
Example 3.15 Let X be a one-sided shift. The complexity function
![]() $p_X$
is defined on positive integers, which sends every
$p_X$
is defined on positive integers, which sends every
![]() $n\geq 1$
to the number of finite words in
$n\geq 1$
to the number of finite words in
![]() $\mathcal {L}(X)$
of length n. Namely,
$\mathcal {L}(X)$
of length n. Namely,
We say that X has a bounded complexity growth if there exists
![]() $K>0$
such that
$K>0$
such that
for all
![]() $n\geq 1$
. Then every minimal one-sided shift space with a bounded complexity growth has property (**), as is shown in Proposition 3.16.
$n\geq 1$
. Then every minimal one-sided shift space with a bounded complexity growth has property (**), as is shown in Proposition 3.16.
Proposition 3.16 If X is a minimal one-sided shift space with a bounded complexity growth, then X has property (**).
Proof It suffices to show that X has only finitely many left special elements. Let
![]() $K\in \mathbb {N}$
be a growth bound of X. We actually have
$K\in \mathbb {N}$
be a growth bound of X. We actually have
![]() $\#\mathrm{Sp}_\mathrm{l}(X)\leq K$
.
$\#\mathrm{Sp}_\mathrm{l}(X)\leq K$
.
If not, then we take
![]() $K+1$
distinct points
$K+1$
distinct points
![]() $\{\omega ^1,\ldots ,\omega ^{K+1}\}\subset \mathrm{Sp}_\mathrm{l}(X)$
and an integer
$\{\omega ^1,\ldots ,\omega ^{K+1}\}\subset \mathrm{Sp}_\mathrm{l}(X)$
and an integer
![]() $N\in \mathbb {N}$
such that the following
$N\in \mathbb {N}$
such that the following
![]() $K+1$
finite words
$K+1$
finite words
are distinct. Note that these finite words are all of length
![]() $N+1$
and each of which can be extended to the left in at least two different ways. This immediately follows that
$N+1$
and each of which can be extended to the left in at least two different ways. This immediately follows that
a contradiction. The proposition follows.
3.4 Covers of one-sided shift spaces
Definition 3.17 We use
![]() $\mathcal {I}$
to denote the set
$\mathcal {I}$
to denote the set
![]() $\{(k,l)\in \mathbb {N}\times \mathbb {N}: 1\leq k\leq l\}$
and
$\{(k,l)\in \mathbb {N}\times \mathbb {N}: 1\leq k\leq l\}$
and
![]() $\mathcal {D}$
its diagonal
$\mathcal {D}$
its diagonal
![]() $\{(k,k)\in \mathcal {I}: k\geq 1\}$
. The partial order
$\{(k,k)\in \mathcal {I}: k\geq 1\}$
. The partial order
![]() $\preceq $
on
$\preceq $
on
![]() $\mathcal {I}$
is defined by
$\mathcal {I}$
is defined by
For the later use, we prove a lemma first.
Lemma 3.18 Let
![]() $\mathcal {F}\subset \mathcal {I}$
be an infinite set. Then
$\mathcal {F}\subset \mathcal {I}$
be an infinite set. Then
![]() ${\mathcal F}$
has an infinite subchain, or in other words, an infinite totally ordered subset of
${\mathcal F}$
has an infinite subchain, or in other words, an infinite totally ordered subset of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Proof Take
![]() $(k_0,l_0)\in \mathcal {F}$
satisfying
$(k_0,l_0)\in \mathcal {F}$
satisfying
Set
![]() $\mathcal {F}_0=\{(k,l)\in \mathcal {F}: k\leq k_0\}$
. Then
$\mathcal {F}_0=\{(k,l)\in \mathcal {F}: k\leq k_0\}$
. Then
![]() $\mathcal {F}_0$
is nonempty. If
$\mathcal {F}_0$
is nonempty. If
![]() $\mathcal {F}\setminus {\mathcal F}_0\neq \varnothing $
, then take
$\mathcal {F}\setminus {\mathcal F}_0\neq \varnothing $
, then take
![]() $(k_1,l_1)\in {\mathcal F}\setminus {\mathcal F}_0$
such that
$(k_1,l_1)\in {\mathcal F}\setminus {\mathcal F}_0$
such that
and set
![]() ${\mathcal F}_1=\{(k,l)\in {\mathcal F}\setminus {\mathcal F}_0: k\leq k_1\}$
. By repeating this step, we are given a sequence of sets
${\mathcal F}_1=\{(k,l)\in {\mathcal F}\setminus {\mathcal F}_0: k\leq k_1\}$
. By repeating this step, we are given a sequence of sets
![]() $\{{\mathcal F}_n\}_{n\ge 0}$
. If each of
$\{{\mathcal F}_n\}_{n\ge 0}$
. If each of
![]() ${\mathcal F}_n$
is finite, then every
${\mathcal F}_n$
is finite, then every
![]() ${\mathcal F}_n$
is nonempty, and this is when
${\mathcal F}_n$
is nonempty, and this is when
![]() $\{(k_n,l_n)\}$
becomes an infinite chain. Conversely, if one of
$\{(k_n,l_n)\}$
becomes an infinite chain. Conversely, if one of
![]() ${\mathcal F}_n$
is infinite, say,
${\mathcal F}_n$
is infinite, say,
![]() ${\mathcal F}_N$
, then by a partition of
${\mathcal F}_N$
, then by a partition of
![]() ${\mathcal F}_N$
into the following
${\mathcal F}_N$
into the following
![]() $k_{N+1}-k_N$
parts:
$k_{N+1}-k_N$
parts:
we see that there exists one of
![]() $O_k^N$
being infinite, which is a chain as well.
$O_k^N$
being infinite, which is a chain as well.
As in [Reference Brix and Carlsen4], for every
![]() $(k,l)\in \mathcal {I}$
, we define an equivalence relation
$(k,l)\in \mathcal {I}$
, we define an equivalence relation
![]() $\stackrel {k,l}{\sim }$
on X by
$\stackrel {k,l}{\sim }$
on X by
We write
![]() $_k[x]_l$
for the
$_k[x]_l$
for the
![]() $\stackrel {k,l}{\sim }$
equivalence class of x and
$\stackrel {k,l}{\sim }$
equivalence class of x and
![]() $_kX_l$
the set of
$_kX_l$
the set of
![]() $\stackrel {k,l}{\sim }$
equivalence classes. It is clear that
$\stackrel {k,l}{\sim }$
equivalence classes. It is clear that
![]() $_kX_l$
is finite. We then have a projective system
$_kX_l$
is finite. We then have a projective system
for all
![]() $(k_1,l_1)\preceq (k_2,l_2)$
.
$(k_1,l_1)\preceq (k_2,l_2)$
.
Definition 3.19 (Cf. [Reference Brix and Carlsen4, Definition 2.1])
Let X be a one-sided shift space with
![]() $\sigma (X)=X$
. By the cover
$\sigma (X)=X$
. By the cover
![]() $\widetilde {X}$
of X, we mean the projective limit
$\widetilde {X}$
of X, we mean the projective limit
![]() $\mathop {\lim }\limits _{\longleftarrow }({}_kX_l, {}_{(k,l)}Q_{(k',l')})$
. The shift operation
$\mathop {\lim }\limits _{\longleftarrow }({}_kX_l, {}_{(k,l)}Q_{(k',l')})$
. The shift operation
![]() $\sigma _{\widetilde {X}}$
on
$\sigma _{\widetilde {X}}$
on
![]() $\widetilde {X}$
is defined so that
$\widetilde {X}$
is defined so that
![]() ${}_k\sigma _{\widetilde {X}}(\tilde {x})_l={}_k[\sigma ({}_{k+1}\tilde {x}_l)]_l$
where
${}_k\sigma _{\widetilde {X}}(\tilde {x})_l={}_k[\sigma ({}_{k+1}\tilde {x}_l)]_l$
where
![]() ${}_{k+1}\tilde {x}_l$
is a representative of a
${}_{k+1}\tilde {x}_l$
is a representative of a
![]() $\stackrel {k+1,l}{\sim }$
-equivalence relation class in
$\stackrel {k+1,l}{\sim }$
-equivalence relation class in
![]() $\tilde {x}$
.
$\tilde {x}$
.
The following sets give a base for the topology of
![]() $\widetilde {X}$
:
$\widetilde {X}$
:
for
![]() $z\in X$
and
$z\in X$
and
![]() $(k,l)\in \mathcal {I}$
. It is known that
$(k,l)\in \mathcal {I}$
. It is known that
![]() $\sigma _{\widetilde {X}}$
is a surjective local homeomorphism (see [Reference Brix and Carlsen4] for details).
$\sigma _{\widetilde {X}}$
is a surjective local homeomorphism (see [Reference Brix and Carlsen4] for details).
Definition 3.20 (Cf. [Reference Brix and Carlsen4, Definition 2.1])
Let
![]() $\pi _X: \widetilde {X}\to X$
to be the map which sends each
$\pi _X: \widetilde {X}\to X$
to be the map which sends each
![]() $\tilde {x}\in \widetilde {X}$
to a point
$\tilde {x}\in \widetilde {X}$
to a point
![]() $x=\pi (\tilde {x})$
so that
$x=\pi (\tilde {x})$
so that
![]() $x_{[0,k)}$
are determined uniquely by
$x_{[0,k)}$
are determined uniquely by
![]() $({}_k\tilde {x}_l)_{[0,k)}$
for every
$({}_k\tilde {x}_l)_{[0,k)}$
for every
![]() $(k,l)\in \mathcal {I}$
. Define
$(k,l)\in \mathcal {I}$
. Define
![]() $\imath _X: X\to \widetilde {X}$
by
$\imath _X: X\to \widetilde {X}$
by
![]() ${}_k\imath _X(x)_l={}_k[x]_l$
for every
${}_k\imath _X(x)_l={}_k[x]_l$
for every
![]() $(k,l)\in \mathcal {I}$
.
$(k,l)\in \mathcal {I}$
.
In fact,
![]() $\pi _X$
is a continuous surjective factor map from
$\pi _X$
is a continuous surjective factor map from
![]() $(\widetilde {X},\sigma _{\widetilde {X}})$
to
$(\widetilde {X},\sigma _{\widetilde {X}})$
to
![]() $(X,\sigma )$
and
$(X,\sigma )$
and
![]() $\imath _X$
is an injective map (not necessarily continuous) such that
$\imath _X$
is an injective map (not necessarily continuous) such that
![]() $\pi _X\circ \imath _X=\mathrm { id}_X$
.
$\pi _X\circ \imath _X=\mathrm { id}_X$
.
Before the sequel, we recall the following lemmas.
Lemma 3.21 (Cf. [Reference Brix3, Lemma 4.2])
Let X be a one-sided shift space. Any isolated point in the cover
![]() $\widetilde {X}$
is contained in the image of
$\widetilde {X}$
is contained in the image of
![]() $\imath _X$
and each fiber
$\imath _X$
and each fiber
![]() $\pi _{X}^{-1}(\{x\})$
contains at most one isolated point. In particular, if
$\pi _{X}^{-1}(\{x\})$
contains at most one isolated point. In particular, if
![]() $x\in X$
is isolated in past equivalence, then
$x\in X$
is isolated in past equivalence, then
![]() $\imath _X(x)$
is an isolated point in
$\imath _X(x)$
is an isolated point in
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
Lemma 3.22 (Cf. [Reference Brix3, Lemma 4.4])
Let X be a one-sided shift space. Suppose that
![]() $x\in X$
has a unique past, then any
$x\in X$
has a unique past, then any
![]() $\tilde {x}\in \pi ^{-1}_X(\{x\})$
also has a unique past.
$\tilde {x}\in \pi ^{-1}_X(\{x\})$
also has a unique past.
We also note the following lemmas for the later use.
Lemma 3.23 Let X be a one-sided shift space with property (**). Suppose that
![]() $\omega ,\omega '\in X$
are left special elements, and
$\omega ,\omega '\in X$
are left special elements, and
![]() $\{(k_m,l_m)\}_{m\ge 1}$
is an infinite sequence in
$\{(k_m,l_m)\}_{m\ge 1}$
is an infinite sequence in
![]() $\mathcal {I}$
where
$\mathcal {I}$
where
![]() $\{k_m\}_{m\ge 1}$
is an unbounded sequence with
$\{k_m\}_{m\ge 1}$
is an unbounded sequence with
![]() $k_m<k_{m+1}$
for all
$k_m<k_{m+1}$
for all
![]() $m\geq 1$
. Assume that to every
$m\geq 1$
. Assume that to every
![]() $m\geq 1$
, an integer
$m\geq 1$
, an integer
![]() $0\leq n_{(k_m,l_m)}<l_m$
is associated such that
$0\leq n_{(k_m,l_m)}<l_m$
is associated such that
for all
![]() $m\geq 1$
. Then the sequence
$m\geq 1$
. Then the sequence
![]() $\{n_{(k_m,l_m)}\}_{m\ge 1}$
is unbounded.
$\{n_{(k_m,l_m)}\}_{m\ge 1}$
is unbounded.
Proof Assume that
![]() $\{n_{(k_m,l_m)}\}_{m\ge 1}$
is bounded. Then there exists an infinite subsequence
$\{n_{(k_m,l_m)}\}_{m\ge 1}$
is bounded. Then there exists an infinite subsequence
![]() $\{(k_{m_i}, l_{m_i})\}_{i\ge 1}$
and an
$\{(k_{m_i}, l_{m_i})\}_{i\ge 1}$
and an
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
By passing to the subsequence
![]() $\{(k_{m_i}, l_{m_i})\}_{i\ge 1}$
and checking the equality of
$\{(k_{m_i}, l_{m_i})\}_{i\ge 1}$
and checking the equality of
![]() $P_{l_{m_i}}$
, we assume, without loss of generality, that
$P_{l_{m_i}}$
, we assume, without loss of generality, that
![]() $n_{(k_m,l_m)}=n$
for some n and all
$n_{(k_m,l_m)}=n$
for some n and all
![]() $m\ge 1$
. Note that
$m\ge 1$
. Note that
![]() $0\leq n<l_m$
. Now, we have
$0\leq n<l_m$
. Now, we have
for all
![]() $m\ge 1$
. The condition
$m\ge 1$
. The condition
![]() $k_m<k_{m+1}$
together with the property (**) then infers that
$k_m<k_{m+1}$
together with the property (**) then infers that
for all
![]() $m\ge 1$
. Also note that because
$m\ge 1$
. Also note that because
![]() $\omega $
is not periodic, there are infinitely many distinct finite words
$\omega $
is not periodic, there are infinitely many distinct finite words
![]() $\omega _{[k_m,k_{m+1}]}$
and we just assume that
$\omega _{[k_m,k_{m+1}]}$
and we just assume that
![]() $\omega _{[k_m,k_{m+1}]}$
are all distinct without loss of generality.
$\omega _{[k_m,k_{m+1}]}$
are all distinct without loss of generality.
The condition
![]() $0\leq n< l_m$
follows that
$0\leq n< l_m$
follows that
![]() $\#P_{l_m}(\sigma ^{n}(\omega '))\ge 2$
, and therefore
$\#P_{l_m}(\sigma ^{n}(\omega '))\ge 2$
, and therefore
for all
![]() $m\ge 1$
. This immediately tells us that every
$m\ge 1$
. This immediately tells us that every
![]() $\omega _{[k_m,k_{m+1})}\sigma ^{n}(\omega ')$
lies on the forward orbit of some left special element. However, since
$\omega _{[k_m,k_{m+1})}\sigma ^{n}(\omega ')$
lies on the forward orbit of some left special element. However, since
![]() $w_{[k_m,k_{m+1}]}\sigma ^n(\omega ')$
are distinct points lying in the backward orbit of
$w_{[k_m,k_{m+1}]}\sigma ^n(\omega ')$
are distinct points lying in the backward orbit of
![]() $\sigma ^n(\omega ')$
, we will then have infinitely many distinct special left elements, which contradicts to the assumption that X has property (**).
$\sigma ^n(\omega ')$
, we will then have infinitely many distinct special left elements, which contradicts to the assumption that X has property (**).
Lemma 3.24 Let X be a minimal one-sided shift with property (**), and let
![]() $x\in X$
. If x has a totally unique past, then
$x\in X$
. If x has a totally unique past, then
![]() $\imath _X(x)\in \widetilde {X}$
is not isolated. Consequently,
$\imath _X(x)\in \widetilde {X}$
is not isolated. Consequently,
![]() $\pi _X^{-1}(\{x\})$
contains no isolated point for any x having a totally unique past.
$\pi _X^{-1}(\{x\})$
contains no isolated point for any x having a totally unique past.
Proof Let
![]() $z\in X$
, and let
$z\in X$
, and let
![]() $(k,l)\in \mathcal {I}$
be so that
$(k,l)\in \mathcal {I}$
be so that
![]() $\imath _X(x)\in U(z,k,l)$
. Then
$\imath _X(x)\in U(z,k,l)$
. Then
![]() $z\stackrel {k,l}{\sim }x$
. Denote
$z\stackrel {k,l}{\sim }x$
. Denote
![]() $P_l(\sigma ^k(x))=\{\mu x_{[0,k)}\}$
with
$P_l(\sigma ^k(x))=\{\mu x_{[0,k)}\}$
with
![]() $|\mu |=l-k$
. It suffices to find an element
$|\mu |=l-k$
. It suffices to find an element
![]() $\tilde {x}$
in
$\tilde {x}$
in
![]() $\widetilde {X}$
such that
$\widetilde {X}$
such that
![]() $z\stackrel {k,l}{\sim }{}_k\tilde {x}_l$
but
$z\stackrel {k,l}{\sim }{}_k\tilde {x}_l$
but
![]() ${}_{k'}\tilde {x}_{l'}\stackrel {k',l'}{\nsim }x$
for some
${}_{k'}\tilde {x}_{l'}\stackrel {k',l'}{\nsim }x$
for some
![]() $(k',l')\in \mathcal {I}$
.
$(k',l')\in \mathcal {I}$
.
Let
![]() $\omega _{\mathfrak {j}}$
be an arbitrary
$\omega _{\mathfrak {j}}$
be an arbitrary
![]() $\mathfrak {j}$
-maximal element for some
$\mathfrak {j}$
-maximal element for some
![]() $\mathfrak {j}\in \mathcal {J}_X$
. Since X is minimal, then
$\mathfrak {j}\in \mathcal {J}_X$
. Since X is minimal, then
![]() $\mu x_{[0,k)}$
occurs infinitely many times in the forward orbit of
$\mu x_{[0,k)}$
occurs infinitely many times in the forward orbit of
![]() $\omega _{\mathfrak {j}}$
. Take
$\omega _{\mathfrak {j}}$
. Take
![]() $L\in \mathbb {N}$
sufficiently large so that
$L\in \mathbb {N}$
sufficiently large so that
Set
![]() $\tilde {x}=\imath _X(\sigma ^{L+l-k}(\omega _{\mathfrak {j}}))$
. Then
$\tilde {x}=\imath _X(\sigma ^{L+l-k}(\omega _{\mathfrak {j}}))$
. Then
![]() $(\sigma ^{L+l-k}(\omega _{\mathfrak {j}}))_{[0,k)}=x_{[0,k)}$
and
$(\sigma ^{L+l-k}(\omega _{\mathfrak {j}}))_{[0,k)}=x_{[0,k)}$
and
![]() $P_l(\sigma ^{L+l}(\omega _{\mathfrak {j}}))=\{\mu x_{[0,k)}\}$
. This verifies
$P_l(\sigma ^{L+l}(\omega _{\mathfrak {j}}))=\{\mu x_{[0,k)}\}$
. This verifies
![]() ${}_kx_l\stackrel {k,l}{\sim }z$
. However, it is clear that
${}_kx_l\stackrel {k,l}{\sim }z$
. However, it is clear that
![]() ${}_{k'}\tilde {x}_{l'}\stackrel {k',l'}{\nsim }x$
for some sufficiently large
${}_{k'}\tilde {x}_{l'}\stackrel {k',l'}{\nsim }x$
for some sufficiently large
![]() $l'$
, since
$l'$
, since
![]() $\sigma ^L(\omega _{\mathfrak {j}})$
sits in the forward orbit of a left special element.
$\sigma ^L(\omega _{\mathfrak {j}})$
sits in the forward orbit of a left special element.
4 The description of covers
In this section, X is always assumed to be a one-sided minimal shift space over the alphabet
![]() $\mathcal {A}=\{0,1\}$
, having property (**). We will, as before, still use
$\mathcal {A}=\{0,1\}$
, having property (**). We will, as before, still use
![]() $\underline {X}$
to denote the corresponding two-sided shift space. Note that
$\underline {X}$
to denote the corresponding two-sided shift space. Note that
![]() $\underline {X}$
is also minimal. We also remark that similar conclusions can be drawn for an arbitrary finite alphabet
$\underline {X}$
is also minimal. We also remark that similar conclusions can be drawn for an arbitrary finite alphabet
![]() $\mathcal {A}$
, but we instead restrict in this paper to the binary shifts for the simplicity of formulations.
$\mathcal {A}$
, but we instead restrict in this paper to the binary shifts for the simplicity of formulations.
First, we point out the isolated points in
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
4.1 Isolated points in cover
Theorem 4.1 The set of isolated points in
![]() $\widetilde {X}$
is dense in
$\widetilde {X}$
is dense in
![]() $\widetilde {X}$
, which is exactly
$\widetilde {X}$
, which is exactly
 $$\begin{align*}\imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\!,\end{align*}$$
$$\begin{align*}\imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\!,\end{align*}$$
where
![]() $\omega _{\mathfrak {j}}$
’s are the unique
$\omega _{\mathfrak {j}}$
’s are the unique
![]() $\mathfrak {j}$
-maximal elements.
$\mathfrak {j}$
-maximal elements.
Proof Write
![]() $I(\widetilde {X})$
for the set of isolated points in
$I(\widetilde {X})$
for the set of isolated points in
![]() $\widetilde {X}$
. We know from Lemma 3.24 that every isolated point of
$\widetilde {X}$
. We know from Lemma 3.24 that every isolated point of
![]() $\widetilde {X}$
has the form
$\widetilde {X}$
has the form
![]() $\imath _X(x)$
for some
$\imath _X(x)$
for some
![]() $x\in X$
, which does not have a totally unique past. This means
$x\in X$
, which does not have a totally unique past. This means
![]() $x\in \mathrm{Orb}_{\sigma }(\omega )$
for some
$x\in \mathrm{Orb}_{\sigma }(\omega )$
for some
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
. Assume now that
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
. Assume now that
![]() $\omega \in \mathfrak {j}_0$
, where
$\omega \in \mathfrak {j}_0$
, where
![]() $\mathfrak {j}_0$
is one of right tail equivalence classes. By the definition of
$\mathfrak {j}_0$
is one of right tail equivalence classes. By the definition of
![]() $\mathfrak {j}$
-maximal elements, we immediately see that
$\mathfrak {j}$
-maximal elements, we immediately see that
![]() $x\in \mathrm{Orb}_\sigma (\omega _{\mathfrak {j}_0})$
. This implies the inclusion
$x\in \mathrm{Orb}_\sigma (\omega _{\mathfrak {j}_0})$
. This implies the inclusion
 $$\begin{align*}I(\widetilde{X})\subset \imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\!.\end{align*}$$
$$\begin{align*}I(\widetilde{X})\subset \imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\!.\end{align*}$$
Conversely, according to the proof of Lemma 3.8, for every
![]() $\mathfrak {j}\in \mathcal {J}_X$
, there is a point
$\mathfrak {j}\in \mathcal {J}_X$
, there is a point
![]() $z\in \mathrm{Orb}_{\sigma }^+(\omega _{\mathfrak {j}})$
isolated in past equivalence, which makes, from Lemma 3.21,
$z\in \mathrm{Orb}_{\sigma }^+(\omega _{\mathfrak {j}})$
isolated in past equivalence, which makes, from Lemma 3.21,
![]() $\imath _X(z)$
an isolated point in
$\imath _X(z)$
an isolated point in
![]() $\widetilde {X}$
. On the other hand, recall that as a local homeomorphism,
$\widetilde {X}$
. On the other hand, recall that as a local homeomorphism,
![]() $\sigma _{\widetilde {X}}$
preserves isolatedness and nonisolatedness, which follows that every point in
$\sigma _{\widetilde {X}}$
preserves isolatedness and nonisolatedness, which follows that every point in
![]() $\imath (\mathrm{Orb}_\sigma (\omega _{\mathfrak {j}}))$
is isolated in
$\imath (\mathrm{Orb}_\sigma (\omega _{\mathfrak {j}}))$
is isolated in
![]() $\widetilde {X}$
. Since
$\widetilde {X}$
. Since
![]() $\mathfrak {j}$
is arbitrary,
$\mathfrak {j}$
is arbitrary,
 $$\begin{align*}\imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\subset I(\widetilde{X}).\end{align*}$$
$$\begin{align*}\imath\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})\right)\subset I(\widetilde{X}).\end{align*}$$
This proves the second assertion. We now show that the set of isolated points in
![]() $\widetilde {X}$
is dense. Let
$\widetilde {X}$
is dense. Let
![]() $z\in X$
and
$z\in X$
and
![]() $(k,l)\in \mathcal {I}$
. To show the density, it suffices to take
$(k,l)\in \mathcal {I}$
. To show the density, it suffices to take
![]() $x\in \mathrm{Orb}(\omega _{\mathfrak {j}})$
such that
$x\in \mathrm{Orb}(\omega _{\mathfrak {j}})$
such that
![]() $z\stackrel {k,l}{\sim }x$
for some
$z\stackrel {k,l}{\sim }x$
for some
![]() $\mathfrak {j}\in \mathcal {J}_X$
. We may assume
$\mathfrak {j}\in \mathcal {J}_X$
. We may assume
![]() $z\notin \mathrm{Orb}_\sigma (\omega _{\mathfrak {j}})$
for all
$z\notin \mathrm{Orb}_\sigma (\omega _{\mathfrak {j}})$
for all
![]() $\mathfrak {j}\in \mathcal {J}_X$
. The argument of the existence of such x is then exactly the same as that of Lemma 3.24.
$\mathfrak {j}\in \mathcal {J}_X$
. The argument of the existence of such x is then exactly the same as that of Lemma 3.24.
Corollary 4.2 There are precisely
![]() $\mathfrak {n}_X$
distinct discrete orbits in
$\mathfrak {n}_X$
distinct discrete orbits in
![]() $\widetilde {X}$
each of which forms an open invariant subspace
$\widetilde {X}$
each of which forms an open invariant subspace
![]() $\widetilde {X}$
, where
$\widetilde {X}$
, where
![]() $\mathfrak {n}_X=\#\mathcal {J}_X$
is the number of right tail equivalence classes in
$\mathfrak {n}_X=\#\mathcal {J}_X$
is the number of right tail equivalence classes in
![]() $\mathrm{Sp}_\mathrm{l}(X)$
. The union of these isolated orbits forms an open dense subset in
$\mathrm{Sp}_\mathrm{l}(X)$
. The union of these isolated orbits forms an open dense subset in
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
4.2 The surjective factor
 $\pi _X$
$\pi _X$
Recall that for every
![]() $\mathfrak {j}\in \mathcal {J}_X$
, the set
$\mathfrak {j}\in \mathcal {J}_X$
, the set
![]() $U_{\mathfrak {j}}$
is defined to be
$U_{\mathfrak {j}}$
is defined to be
Remark 4.3 Elements in
![]() $U_{\mathfrak {j}}$
are called adjusted and
$U_{\mathfrak {j}}$
are called adjusted and
![]() $\mathfrak {j}$
-maximal elements
$\mathfrak {j}$
-maximal elements
![]() $\omega _{\mathfrak {j}}$
are called cofinal in [Reference Carlsen and Eilers8]. It is easy to see that
$\omega _{\mathfrak {j}}$
are called cofinal in [Reference Carlsen and Eilers8]. It is easy to see that
![]() $U_{\mathfrak {j}}$
is nonempty for every
$U_{\mathfrak {j}}$
is nonempty for every
![]() $\mathfrak {j}\in \mathcal {J}_X$
.
$\mathfrak {j}\in \mathcal {J}_X$
.
Lemma 4.4 For every
![]() $\mathfrak {j}\in \mathcal {J}_X$
and
$\mathfrak {j}\in \mathcal {J}_X$
and
![]() $\omega \in U_{\mathfrak {j}}$
,
$\omega \in U_{\mathfrak {j}}$
,
![]() $\#\pi _X^{-1}(\{\omega \})=3$
.
$\#\pi _X^{-1}(\{\omega \})=3$
.
Proof We first show that there are at least three distinct elements in
![]() $\pi _X^{-1}(\{\omega \})$
. The construction below of these three preimages is similar to that of [Reference Brix3].
$\pi _X^{-1}(\{\omega \})$
. The construction below of these three preimages is similar to that of [Reference Brix3].
For every
![]() ${\alpha }\in \{0,1\}$
and
${\alpha }\in \{0,1\}$
and
![]() $(k,l)\in \mathcal {I}\setminus \mathcal {D}$
, let
$(k,l)\in \mathcal {I}\setminus \mathcal {D}$
, let
![]() $\mu _{(k,l)}^{\alpha }\in \mathcal {L}(X)$
with
$\mu _{(k,l)}^{\alpha }\in \mathcal {L}(X)$
with
![]() $|\mu _{(k,l)}^{\alpha }|=l-k-1$
be such that
$|\mu _{(k,l)}^{\alpha }|=l-k-1$
be such that
![]() $\mu _{(k,l)}^{\alpha }{\alpha }\omega \in X$
. Note that such finite word
$\mu _{(k,l)}^{\alpha }{\alpha }\omega \in X$
. Note that such finite word
![]() $\mu _{(k,l)}^{\alpha }$
is unique because
$\mu _{(k,l)}^{\alpha }$
is unique because
![]() $\omega \in U_{\mathfrak {j}}$
. Now, since X has property (**), we can take
$\omega \in U_{\mathfrak {j}}$
. Now, since X has property (**), we can take
![]() $x_{(k,l)}^{\alpha }\in X$
satisfying
$x_{(k,l)}^{\alpha }\in X$
satisfying
Define
![]() ${}_kx^{\alpha }_l=\omega _{[0,k)}x_{(k,l)}^{\alpha }$
. Note that for
${}_kx^{\alpha }_l=\omega _{[0,k)}x_{(k,l)}^{\alpha }$
. Note that for
![]() ${\alpha }=0,1$
, we have
${\alpha }=0,1$
, we have
We now define representatives on each
![]() $(k,k)\in \mathcal {D}$
. Take
$(k,k)\in \mathcal {D}$
. Take
![]() $x_{(k,k)}^{\alpha }\in X$
with
$x_{(k,k)}^{\alpha }\in X$
with
![]() $P_k(x_{(k,k)}^{\alpha })=\{\omega _{[0,k)}\}$
. Let
$P_k(x_{(k,k)}^{\alpha })=\{\omega _{[0,k)}\}$
. Let
![]() ${}_kx_k^{\alpha }=\omega _{[0,k)}x_{(k,k)}^{\alpha }$
. Now, for
${}_kx_k^{\alpha }=\omega _{[0,k)}x_{(k,k)}^{\alpha }$
. Now, for
![]() ${\alpha }=0,1$
, set
${\alpha }=0,1$
, set
![]() $\tilde {x}^{\alpha }\in \widetilde {X}$
satisfying
$\tilde {x}^{\alpha }\in \widetilde {X}$
satisfying
It is clear that
![]() $\pi (\tilde {x}^{\alpha })=\omega $
and
$\pi (\tilde {x}^{\alpha })=\omega $
and
![]() $\{\imath (\omega ), \tilde {x}^0, \tilde {x}^1\}$
are three distinct elements. It is now enough to show that
$\{\imath (\omega ), \tilde {x}^0, \tilde {x}^1\}$
are three distinct elements. It is now enough to show that
![]() $\tilde {x}^{\alpha }$
are well defined. We will only verify the case for
$\tilde {x}^{\alpha }$
are well defined. We will only verify the case for
![]() ${\alpha }=0$
, since the other one is exactly the same. For the simplicity of notations, we drop all the superscripts and abbreviate
${\alpha }=0$
, since the other one is exactly the same. For the simplicity of notations, we drop all the superscripts and abbreviate
![]() $\tilde {x}^0$
to
$\tilde {x}^0$
to
![]() $\tilde {x}$
, for instance.
$\tilde {x}$
, for instance.
(i) Let
![]() $(k_1,l_1)\preceq (k_2,l_2)$
be indices in
$(k_1,l_1)\preceq (k_2,l_2)$
be indices in
![]() $\mathcal {I}\setminus \mathcal {D}$
. It is trivial that
$\mathcal {I}\setminus \mathcal {D}$
. It is trivial that
![]() $({}_{k_1}[x]_{l_1})_{[0,k_1)}=\omega _{[0,k_1)}=({}_{k_2}[x]_{l_2})_{[0,k_1)}$
, so it remains to show that
$({}_{k_1}[x]_{l_1})_{[0,k_1)}=\omega _{[0,k_1)}=({}_{k_2}[x]_{l_2})_{[0,k_1)}$
, so it remains to show that
For every
![]() $\nu \in P_{l_1}(\omega _{[k_1,k_2)}x_{(k_2,l_2)})$
,
$\nu \in P_{l_1}(\omega _{[k_1,k_2)}x_{(k_2,l_2)})$
,
![]() $\nu \omega _{[k_1,k_2)}\in P_{k_2-k_1+l_1}(x_{(k_2,l_2)})$
, and since
$\nu \omega _{[k_1,k_2)}\in P_{k_2-k_1+l_1}(x_{(k_2,l_2)})$
, and since
![]() $l_1+k_2-k_1\leq l_2$
,
$l_1+k_2-k_1\leq l_2$
,
![]() $\nu \omega _{[k_1,k_2)}$
is the suffix of an element in
$\nu \omega _{[k_1,k_2)}$
is the suffix of an element in
![]() $P_{l_2}(x_{(k_2,l_2)})$
, which follows
$P_{l_2}(x_{(k_2,l_2)})$
, which follows
![]() $\nu =\nu '0\omega _{[0,k_1)}$
, where
$\nu =\nu '0\omega _{[0,k_1)}$
, where
![]() $\nu '$
is the suffix of
$\nu '$
is the suffix of
![]() $\mu _{(k_2,l_2)}$
with length
$\mu _{(k_2,l_2)}$
with length
![]() $l_1-k_1-1$
. However, as
$l_1-k_1-1$
. However, as
![]() $0\omega $
has a unique past,
$0\omega $
has a unique past,
![]() $\nu '=\mu _{(k_1,l_1)}$
.
$\nu '=\mu _{(k_1,l_1)}$
.
(ii) Let
![]() $(k_1,k_1)\in \mathcal {D}$
and
$(k_1,k_1)\in \mathcal {D}$
and
![]() $(k_2,l_2)\in \mathcal {I}\setminus \mathcal {D}$
with
$(k_2,l_2)\in \mathcal {I}\setminus \mathcal {D}$
with
![]() $k_1\leq k_2$
. We shall confirm that
$k_1\leq k_2$
. We shall confirm that
Since for every
![]() $\nu \in P_{k_1}(\omega _{[k_1,k_2)}x_{(k_2,l_2)}$
,
$\nu \in P_{k_1}(\omega _{[k_1,k_2)}x_{(k_2,l_2)}$
,
![]() $\nu \omega _{[k_1,k_2)}\in P_{k_2}(x_{(k_2,l_2)})$
. The inequality
$\nu \omega _{[k_1,k_2)}\in P_{k_2}(x_{(k_2,l_2)})$
. The inequality
![]() $k_2\leq l_2$
infers that
$k_2\leq l_2$
infers that
![]() $\nu \omega _{[k_1,k_2)}$
is the suffix of some element in
$\nu \omega _{[k_1,k_2)}$
is the suffix of some element in
![]() $P_{l_2}(x_{(k_2,l_2)})=\{\mu _{(k_2,l_2)}0\omega _{[0,k_2)}\}$
, which has to be
$P_{l_2}(x_{(k_2,l_2)})=\{\mu _{(k_2,l_2)}0\omega _{[0,k_2)}\}$
, which has to be
![]() $\omega _{[0,k_2)}$
. Therefore,
$\omega _{[0,k_2)}$
. Therefore,
![]() $\nu =\omega _{[0,k_1)}$
.
$\nu =\omega _{[0,k_1)}$
.
(iii) The case for
![]() $(k_1, k_1), (k_2,k_2)\in \mathcal {D}$
where
$(k_1, k_1), (k_2,k_2)\in \mathcal {D}$
where
![]() $k_1\leq k_2$
is quite similar to the case (ii) and hence we omit the verification.
$k_1\leq k_2$
is quite similar to the case (ii) and hence we omit the verification.
Now, we have shown
![]() $\#\pi _X^{-1}(\{\omega \})\geq 3$
. We next prove that these are exactly the only three elements on this fiber.
$\#\pi _X^{-1}(\{\omega \})\geq 3$
. We next prove that these are exactly the only three elements on this fiber.
Take
![]() $\tilde {x}\in \pi ^{-1}_X(\omega )$
and write
$\tilde {x}\in \pi ^{-1}_X(\omega )$
and write
![]() $_k\tilde {x}_l={}_k[\omega _{[0,k)}x_{(k,l)}]_l$
for some
$_k\tilde {x}_l={}_k[\omega _{[0,k)}x_{(k,l)}]_l$
for some
![]() $x_{(k,l)}\in X$
.
$x_{(k,l)}\in X$
.
Claim. If there exists
![]() $(k_0,l_0)\in \mathcal {I}$
such that
$(k_0,l_0)\in \mathcal {I}$
such that
![]() $\# P_{l_0}(x_{(k_0,l_0)})=1$
, then
$\# P_{l_0}(x_{(k_0,l_0)})=1$
, then
![]() $\tilde {x}\in \{\tilde {x}^0, \tilde {x}^1\}$
.
$\tilde {x}\in \{\tilde {x}^0, \tilde {x}^1\}$
.
This is immediate. Suppose
![]() $P_{l_0}(x_{(k_0,l_0)})=\{\mu 0\omega _{[0,k_0)}\}$
, then every
$P_{l_0}(x_{(k_0,l_0)})=\{\mu 0\omega _{[0,k_0)}\}$
, then every
![]() $x_{(k',l')}$
with
$x_{(k',l')}$
with
![]() $(k',l')\preceq (k_0,l_0)$
are determined. Also note that for all
$(k',l')\preceq (k_0,l_0)$
are determined. Also note that for all
![]() $(k',l')$
with
$(k',l')$
with
![]() $(k_0,l_0)\preceq (k',l')$
are also unique determined because
$(k_0,l_0)\preceq (k',l')$
are also unique determined because
![]() $0\omega $
has a unique past. Then
$0\omega $
has a unique past. Then
![]() $x_{(k,l)}$
are all determined, because
$x_{(k,l)}$
are all determined, because
![]() $\mathcal {I}$
is directed in the sense that given any two points
$\mathcal {I}$
is directed in the sense that given any two points
![]() $(k',l'), (k",l")\in \mathcal {I}$
, we can always find
$(k',l'), (k",l")\in \mathcal {I}$
, we can always find
![]() $(k"',l"')\in \mathcal {I}$
with
$(k"',l"')\in \mathcal {I}$
with
![]() $(k',l')\preceq (k"',l"')$
and
$(k',l')\preceq (k"',l"')$
and
![]() $(k",l")\preceq (k"',l"')$
.
$(k",l")\preceq (k"',l"')$
.
Now, assume that
![]() $\# P_{l}(x_{(k,l)})\ge 2$
for all
$\# P_{l}(x_{(k,l)})\ge 2$
for all
![]() $(k,l)\in \mathcal {I}$
. We then show that
$(k,l)\in \mathcal {I}$
. We then show that
![]() $\tilde {x}=\imath _X(\omega )$
, which will finish the proof. Fix any
$\tilde {x}=\imath _X(\omega )$
, which will finish the proof. Fix any
![]() $(k_0,l_0)\in \mathcal {I}$
. Note that this leads to the fact that, for every
$(k_0,l_0)\in \mathcal {I}$
. Note that this leads to the fact that, for every
![]() $(k,l)\in \mathcal {I}$
with
$(k,l)\in \mathcal {I}$
with
![]() $(k_0,l_0)\preceq (k,l)$
, there exists
$(k_0,l_0)\preceq (k,l)$
, there exists
![]() $\omega _{(k,l)}\in \mathrm{Sp}_\mathrm{l}(X)$
and integers
$\omega _{(k,l)}\in \mathrm{Sp}_\mathrm{l}(X)$
and integers
![]() $0\leq n_{(k,l)}\leq l-1$
such that
$0\leq n_{(k,l)}\leq l-1$
such that
The finiteness of
![]() $\mathrm{Sp}_\mathrm{l}(X)$
implies that there is
$\mathrm{Sp}_\mathrm{l}(X)$
implies that there is
![]() $\omega '\in \mathrm{Sp}_\mathrm{l}(X)$
and infinitely many
$\omega '\in \mathrm{Sp}_\mathrm{l}(X)$
and infinitely many
![]() $(k_m,l_m)\in \mathcal {I}$
satisfying
$(k_m,l_m)\in \mathcal {I}$
satisfying
![]() $(k_0,l_0)\preceq (k_m,l_m)$
,
$(k_0,l_0)\preceq (k_m,l_m)$
,
![]() $k_m<k_{m+1}$
for all
$k_m<k_{m+1}$
for all
![]() $m\ge 1$
,
$m\ge 1$
,
![]() $\lim _{m\to \infty }k_m=\infty $
, and
$\lim _{m\to \infty }k_m=\infty $
, and
Upon passing to a subsequence, we may assume, according to Lemma 3.18, that
![]() $\{(k_m,l_m)\}_{m\ge 1}$
is a chain in the sense that
$\{(k_m,l_m)\}_{m\ge 1}$
is a chain in the sense that
![]() $(k_m,l_m)\preceq (k_{m'}, l_{m'})$
whenever
$(k_m,l_m)\preceq (k_{m'}, l_{m'})$
whenever
![]() $m\geq m'$
. By the definition of cover, we then have
$m\geq m'$
. By the definition of cover, we then have
Now, Lemma 3.23 applies, indicating that
![]() $n_{(k_m,l_m)}$
is unbounded. Hence, we may assume, without loss of generality, that
$n_{(k_m,l_m)}$
is unbounded. Hence, we may assume, without loss of generality, that
![]() $n_{(k_m,l_m)}\to \infty $
as
$n_{(k_m,l_m)}\to \infty $
as
![]() $m\to \infty $
.
$m\to \infty $
.
On the other hand, from Lemma 3.8, we can take an
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\sigma ^n(\omega ')$
is isolated in l past equivalence whenever
$\sigma ^n(\omega ')$
is isolated in l past equivalence whenever
![]() $l>n\geq N$
. Choose
$l>n\geq N$
. Choose
![]() $M\in \mathbb {N}$
such that
$M\in \mathbb {N}$
such that
![]() $n_{(k_m,l_m)}>N$
whenever
$n_{(k_m,l_m)}>N$
whenever
![]() $m>M$
. This follows that
$m>M$
. This follows that
whenever
![]() $m>M, l>n_{(k_m,l_m)}$
. In particular,
$m>M, l>n_{(k_m,l_m)}$
. In particular,
![]() $x_{(k_m,l_m)}$
is
$x_{(k_m,l_m)}$
is
![]() $l_m$
-isolated because
$l_m$
-isolated because
![]() $l_m>n_{(k_m,l_m)}$
. Then, we know from
$l_m>n_{(k_m,l_m)}$
. Then, we know from
that
![]() $x_{(k_m,l_m)}=\sigma ^{n_{(k_m,l_m)}}(\omega ')=\omega _{[k_m,k_{m+1})}x_{(k_{m+1}, l_{m+1})}$
for all
$x_{(k_m,l_m)}=\sigma ^{n_{(k_m,l_m)}}(\omega ')=\omega _{[k_m,k_{m+1})}x_{(k_{m+1}, l_{m+1})}$
for all
![]() $m>M$
. Finally, since
$m>M$
. Finally, since
![]() $k_1<k_2<\cdots <k_m<k_{m+1}<\cdots $
and
$k_1<k_2<\cdots <k_m<k_{m+1}<\cdots $
and
![]() $\lim _{m\to \infty }k_m=\infty $
, we conclude that for all
$\lim _{m\to \infty }k_m=\infty $
, we conclude that for all
![]() $m>M$
,
$m>M$
,
and therefore
![]() ${}_{k_m}\tilde {x}_{l_m}={}_{k_m}[\omega ]_{l_m}$
. Recall that
${}_{k_m}\tilde {x}_{l_m}={}_{k_m}[\omega ]_{l_m}$
. Recall that
![]() $(k_m,l_m)\succeq (k_0,l_0)$
for every m, we then have
$(k_m,l_m)\succeq (k_0,l_0)$
for every m, we then have
![]() ${}_{k_0}\tilde {x}_{l_0}={}_{k_0}[\omega ]_{l_0}$
. Finally, as the above discussion can be applied to every
${}_{k_0}\tilde {x}_{l_0}={}_{k_0}[\omega ]_{l_0}$
. Finally, as the above discussion can be applied to every
![]() $(k_0,l_0)\,{\in}\, \mathcal {I}$
,
$(k_0,l_0)\,{\in}\, \mathcal {I}$
,
![]() $\tilde {x}=\imath _X(\omega )$
, the lemma follows.
$\tilde {x}=\imath _X(\omega )$
, the lemma follows.
Definition 4.5 Let
![]() $x\in X$
and
$x\in X$
and
![]() $\{z^m\}_{m\leq 0}$
be a sequence in X. We say
$\{z^m\}_{m\leq 0}$
be a sequence in X. We say
![]() $\{z^m\}_{m\leq 0}$
is a directed path terminating at x if
$\{z^m\}_{m\leq 0}$
is a directed path terminating at x if
![]() $z^0=x$
and
$z^0=x$
and
![]() $\sigma (z^{m-1})=z^m$
for all
$\sigma (z^{m-1})=z^m$
for all
![]() $m\leq 0$
. It is not hard to see that for every one-sided shift space X with
$m\leq 0$
. It is not hard to see that for every one-sided shift space X with
![]() $\#\mathrm{Sp}_\mathrm{l}(X)<\infty $
and every
$\#\mathrm{Sp}_\mathrm{l}(X)<\infty $
and every
![]() $x\in X$
, the number of directed paths in X terminating at x is finite. We denote this number by
$x\in X$
, the number of directed paths in X terminating at x is finite. We denote this number by
![]() $\mathfrak {d}(x)$
.
$\mathfrak {d}(x)$
.
It immediately follows that for any fixed nonmaximal element
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
and
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
and
![]() $m_0=\min \{m>0: \sigma ^m(\omega )\in \mathrm{Sp}_\mathrm{l}(X)\}$
, we have that
$m_0=\min \{m>0: \sigma ^m(\omega )\in \mathrm{Sp}_\mathrm{l}(X)\}$
, we have that
Theorem 4.6 For every
![]() $x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
,
$x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
,
Proof First, we verify the situation for which x has a unique past, that is,
![]() $\mathfrak {d}(x)=1$
. This could happen, for example, when x lies in the backward orbit of some
$\mathfrak {d}(x)=1$
. This could happen, for example, when x lies in the backward orbit of some
![]() $\omega \in U_{\mathfrak {j}}$
. Then it is clear that either
$\omega \in U_{\mathfrak {j}}$
. Then it is clear that either
![]() $0x\in X$
or
$0x\in X$
or
![]() $1x\in X$
. In any case, the procedure of Lemma 4.4 defines a nonisolated point in
$1x\in X$
. In any case, the procedure of Lemma 4.4 defines a nonisolated point in
![]() $\pi _X^{-1}(\{x\})$
and an exactly same argument as in Lemma 4.4 shows that
$\pi _X^{-1}(\{x\})$
and an exactly same argument as in Lemma 4.4 shows that
![]() $\#\pi _X^{-1}(\{x\})=2=\mathfrak {d}(x)+1$
.
$\#\pi _X^{-1}(\{x\})=2=\mathfrak {d}(x)+1$
.
For the case when
![]() $x\in \mathrm{Sp}_\mathrm{l}(X)$
, according to the definition of the integer-valued function
$x\in \mathrm{Sp}_\mathrm{l}(X)$
, according to the definition of the integer-valued function
![]() $\mathfrak {d}$
, there are at most
$\mathfrak {d}$
, there are at most
![]() $\mathfrak {d}(x)$
finite prefixes
$\mathfrak {d}(x)$
finite prefixes
with
![]() $|\mu _{(k,l)}^i|=l-k$
for sufficiently large
$|\mu _{(k,l)}^i|=l-k$
for sufficiently large
![]() $(k,l)\in \mathcal {I}$
such that
$(k,l)\in \mathcal {I}$
such that
![]() $\mu _{(k,l)}^ix\in X$
and moreover, for each pair of
$\mu _{(k,l)}^ix\in X$
and moreover, for each pair of
![]() $\mu _{(k,l)}^ix$
and
$\mu _{(k,l)}^ix$
and
![]() $\mu _{(k,l)}^jx$
(
$\mu _{(k,l)}^jx$
(
![]() $i\neq j$
) and every
$i\neq j$
) and every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\mu _{(k,l)}^ix\neq \sigma ^n(\mu _{(k,l)}^jx)$
and
$\mu _{(k,l)}^ix\neq \sigma ^n(\mu _{(k,l)}^jx)$
and
![]() $\mu _{(k,l)}^jx\neq \sigma ^n(\mu _{(k,l)}^ix)$
. Since X has property
$\mu _{(k,l)}^jx\neq \sigma ^n(\mu _{(k,l)}^ix)$
. Since X has property
![]() $(**)$
as assumed, we can take
$(**)$
as assumed, we can take
satisfying
![]() $P_l(x_{(k,l)}^i)=\{\mu _{(k,l)}^ix_{[0,k)}\}$
for
$P_l(x_{(k,l)}^i)=\{\mu _{(k,l)}^ix_{[0,k)}\}$
for
![]() $i=0,1,\ldots , \mathfrak {d}(x)$
.
$i=0,1,\ldots , \mathfrak {d}(x)$
.
Now, an easy adaption of the procedure in Lemma 4.4 defines
![]() $\mathfrak {d}(x)$
distinct elements in
$\mathfrak {d}(x)$
distinct elements in
![]() $\pi _X^{-1}(\{x\})$
such that if
$\pi _X^{-1}(\{x\})$
such that if
![]() $\tilde {x}\in \pi _X^{-1}(\{x\})$
is not one of the points we constructed above, then
$\tilde {x}\in \pi _X^{-1}(\{x\})$
is not one of the points we constructed above, then
![]() $\tilde {x}=\imath _X(x)$
. This proves that for any left special element x in the whole orbit of any maximal left special element
$\tilde {x}=\imath _X(x)$
. This proves that for any left special element x in the whole orbit of any maximal left special element
![]() $\omega _{\mathfrak {j}}$
,
$\omega _{\mathfrak {j}}$
,
Finally, let us consider those elements
![]() $x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
which are not left special. This divides into the following three cases:
$x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
which are not left special. This divides into the following three cases:
-
(i) x lies in the backward orbit of some
 $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
having a unique past.
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
having a unique past. -
(ii) x lies in the forward orbit of some maximal element
 $\omega _{\mathfrak {j}}$
for
$\omega _{\mathfrak {j}}$
for
 $\mathfrak {j}\in \mathcal {J}_X$
.
$\mathfrak {j}\in \mathcal {J}_X$
. -
(iii) There are distinct left special elements
 $\omega ,\omega '$
such that
$\omega ,\omega '$
such that
 $\omega $
lies in the backward orbit of x and
$\omega $
lies in the backward orbit of x and
 $\omega '$
lies in the forward orbit of x.
$\omega '$
lies in the forward orbit of x.
Note that the case (i) has already been included in the first paragraph above. For (ii) and (iii), let
![]() $\omega $
be a left special element and
$\omega $
be a left special element and
Without loss of generality, we may say
![]() $m_0(\omega )=\infty $
if
$m_0(\omega )=\infty $
if
![]() $\omega $
is a maximal element. We now reach (ii) and (iii) by showing that
$\omega $
is a maximal element. We now reach (ii) and (iii) by showing that
for any
![]() $1\leq s<m_0(\omega )$
.
$1\leq s<m_0(\omega )$
.
For this, write
![]() $\pi _X^{-1}(\{\omega \})=\{\imath _X(\omega ), \tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}\}$
, where
$\pi _X^{-1}(\{\omega \})=\{\imath _X(\omega ), \tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}\}$
, where
![]() $\tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}$
are the elements in
$\tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}$
are the elements in
![]() $\pi _X^{-1}(\{\omega \})$
constructed above. We then have
$\pi _X^{-1}(\{\omega \})$
constructed above. We then have
It is clear that these
![]() $\mathfrak {d}(\omega )+1$
elements are distinct and in the preimage of
$\mathfrak {d}(\omega )+1$
elements are distinct and in the preimage of
![]() $\sigma ^s(\omega )$
. Therefore, it suffices to show that there are no more elements in the fiber. Suppose that
$\sigma ^s(\omega )$
. Therefore, it suffices to show that there are no more elements in the fiber. Suppose that
![]() $\tilde {y}\in \pi ^{-1}_X(\{\sigma ^{s}(\omega )\})$
. Since
$\tilde {y}\in \pi ^{-1}_X(\{\sigma ^{s}(\omega )\})$
. Since
![]() $\sigma _{\widetilde {X}}$
is surjective, there exists
$\sigma _{\widetilde {X}}$
is surjective, there exists
![]() $\tilde {z}$
such that
$\tilde {z}$
such that
![]() $\sigma _{\widetilde {X}}^s(\tilde {z})=\tilde {y}$
. Take
$\sigma _{\widetilde {X}}^s(\tilde {z})=\tilde {y}$
. Take
![]() $z=\pi _X(\tilde {z})$
. Since
$z=\pi _X(\tilde {z})$
. Since
![]() $\pi _X$
is a factor,
$\pi _X$
is a factor,
![]() $\sigma ^s(z)=\sigma ^s(\omega )$
. If
$\sigma ^s(z)=\sigma ^s(\omega )$
. If
![]() $z\neq \omega $
, then there exists
$z\neq \omega $
, then there exists
![]() $1\leq j\leq s<m_0(\omega )$
such that
$1\leq j\leq s<m_0(\omega )$
such that
![]() $\sigma ^j(\omega )$
is left special, but this contradicts to the minimality of
$\sigma ^j(\omega )$
is left special, but this contradicts to the minimality of
![]() $m_0$
. Therefore,
$m_0$
. Therefore,
![]() $z=\omega $
and hence
$z=\omega $
and hence
![]() $\tilde {z}\in \{\imath _X(\omega ), \tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}\}$
. This shows that there are no more elements in the fiber. Noting that
$\tilde {z}\in \{\imath _X(\omega ), \tilde {x}^1, \tilde {x}^2, \ldots , \tilde {x}^{\mathfrak {d}(\omega )}\}$
. This shows that there are no more elements in the fiber. Noting that
(ii) and (iii) follow as desired.
For the last part of the subsection, we consider those
![]() $z\in X$
having totally unique past.
$z\in X$
having totally unique past.
Theorem 4.7 Let
![]() $z\in X\setminus \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
. Then
$z\in X\setminus \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
. Then
![]() $\#\pi _X^{-1}(z)=1$
.
$\#\pi _X^{-1}(z)=1$
.
Proof Let
![]() $\tilde {z}\in \widetilde {X}$
with
$\tilde {z}\in \widetilde {X}$
with
![]() $\pi _X(\tilde {z})=z$
. Let us show that
$\pi _X(\tilde {z})=z$
. Let us show that
![]() $\tilde {z}=\imath _X(z)$
. Write
$\tilde {z}=\imath _X(z)$
. Write
![]() ${}_k\tilde {z}_l={}_k[z_{[0,k)}z_{(k,l)}]_l$
. We turn to prove that
${}_k\tilde {z}_l={}_k[z_{[0,k)}z_{(k,l)}]_l$
. We turn to prove that
for all
![]() $(k,l)\in \mathcal {I}$
. Obviously, they have the same initial sections of length k. Therefore, it remains to verify that
$(k,l)\in \mathcal {I}$
. Obviously, they have the same initial sections of length k. Therefore, it remains to verify that
Write
![]() $P_l(z_{[k,\infty )})=\{\mu z_{[0,k)}\}$
where
$P_l(z_{[k,\infty )})=\{\mu z_{[0,k)}\}$
where
![]() $\mu $
is the unique prefix of length
$\mu $
is the unique prefix of length
![]() $l-k$
. We turn to show the following claims to finish the proof.
$l-k$
. We turn to show the following claims to finish the proof.
Claim 1.
![]() $\mu z_{[0,k)}z_{(k,l)}\in X$
: Since z has a unique past, so does
$\mu z_{[0,k)}z_{(k,l)}\in X$
: Since z has a unique past, so does
![]() $\tilde {z}$
. Take the unique
$\tilde {z}$
. Take the unique
![]() $\tilde {z}'\in \widetilde {X}$
so that
$\tilde {z}'\in \widetilde {X}$
so that
![]() $\sigma _{\widetilde {X}}(\tilde {z}')=\tilde {z}$
. Note that this implies
$\sigma _{\widetilde {X}}(\tilde {z}')=\tilde {z}$
. Note that this implies
and hence
![]() $\pi _X(\tilde {z}')=\mu z$
. Denote
$\pi _X(\tilde {z}')=\mu z$
. Denote
![]() $\tilde {z}'={}_k[{}_k\tilde {z}^{\prime }_l]_l$
. We then have
$\tilde {z}'={}_k[{}_k\tilde {z}^{\prime }_l]_l$
. We then have
![]() $({}_l\tilde {z}^{\prime }_l)_{[0,l)}=\mu z_{[0,k)}$
. On the other hand,
$({}_l\tilde {z}^{\prime }_l)_{[0,l)}=\mu z_{[0,k)}$
. On the other hand,
which tells us
![]() $z_{[0,k)}z_{(k,l)}={}_k\tilde {z}_l\stackrel {k,l}{\sim }\sigma ^{l-k}({}_l\tilde {z}^{\prime }_l)$
. Therefore,
$z_{[0,k)}z_{(k,l)}={}_k\tilde {z}_l\stackrel {k,l}{\sim }\sigma ^{l-k}({}_l\tilde {z}^{\prime }_l)$
. Therefore,
Claim 2.
![]() $\# P_l(z_{(k,l)})=1$
: Since z has a totally unique past,
$\# P_l(z_{(k,l)})=1$
: Since z has a totally unique past,
![]() $\sigma ^k(z)$
has a unique past. By Lemma 3.4, we can choose
$\sigma ^k(z)$
has a unique past. By Lemma 3.4, we can choose
![]() $N_1\in \mathbb {N}$
with the following property:
$N_1\in \mathbb {N}$
with the following property:
Set
![]() $N=N_1+k+1$
. Since
$N=N_1+k+1$
. Since
![]() $(N, l+N-k)\succeq (k,l)$
, we have
$(N, l+N-k)\succeq (k,l)$
, we have
which follows that
However, since
![]() $\sigma ^k({}_N\tilde {z}_{l+N-k})=z_kz_{k+1}\cdots z_{N-1}\tilde {z}_{(N,l+N-k)}$
, it has a prefix of length
$\sigma ^k({}_N\tilde {z}_{l+N-k})=z_kz_{k+1}\cdots z_{N-1}\tilde {z}_{(N,l+N-k)}$
, it has a prefix of length
![]() $N-k=N_1+1$
, equal to
$N-k=N_1+1$
, equal to
![]() $\sigma ^k(z)_{[0,N_1]}$
. Therefore, by how we choose
$\sigma ^k(z)_{[0,N_1]}$
. Therefore, by how we choose
![]() $N_1$
, we conclude that
$N_1$
, we conclude that
This completes the proof.
4.3 Nonisolated points in the cover
Theorem 4.8 Let
be the nonisolated points in the cover. Then
![]() $\tilde {\Lambda }_X\cong \underline {X}$
, i.e., there is a canonical conjugacy from
$\tilde {\Lambda }_X\cong \underline {X}$
, i.e., there is a canonical conjugacy from
![]() $(\tilde {\Lambda }_X,\sigma _{\widetilde {X}})$
to
$(\tilde {\Lambda }_X,\sigma _{\widetilde {X}})$
to
![]() $(\underline {X},\sigma )$
, where
$(\underline {X},\sigma )$
, where
![]() $\underline {X}$
is the two-sided shift associated with X.
$\underline {X}$
is the two-sided shift associated with X.
Proof Note that since the set of isolated points is open,
![]() $\tilde {\Lambda }_X$
is closed and invariant. We first show that every element of
$\tilde {\Lambda }_X$
is closed and invariant. We first show that every element of
![]() $\tilde {\Lambda }_X$
has a unique past. For this, by Lemma 3.22, we only need to verify that, for any fixed
$\tilde {\Lambda }_X$
has a unique past. For this, by Lemma 3.22, we only need to verify that, for any fixed
![]() $k>0$
,
$k>0$
,
![]() $\omega \in \mathrm{Sp}_\mathrm{l}(X)$
and
$\omega \in \mathrm{Sp}_\mathrm{l}(X)$
and
![]() $\tilde {z}\in \pi _X^{-1}(\sigma ^k(\omega ))\setminus \{\imath _X(\sigma ^k(\omega ))\}$
,
$\tilde {z}\in \pi _X^{-1}(\sigma ^k(\omega ))\setminus \{\imath _X(\sigma ^k(\omega ))\}$
,
![]() $\tilde {z}$
has a unique past.
$\tilde {z}$
has a unique past.
Denote
![]() $z=\sigma ^k(\omega )$
. Then
$z=\sigma ^k(\omega )$
. Then
![]() $\pi _X(\tilde {z})=z$
. Define
$\pi _X(\tilde {z})=z$
. Define
Note that because
![]() $\omega $
is left special and
$\omega $
is left special and
![]() $z=\sigma ^k(\omega )$
,
$z=\sigma ^k(\omega )$
,
![]() $m_z$
is well defined. Then we claim that the sets
$m_z$
is well defined. Then we claim that the sets
are singletons for
![]() $i=1,2,\ldots ,m_z$
. In fact, for
$i=1,2,\ldots ,m_z$
. In fact, for
![]() $i=1$
, if there are
$i=1$
, if there are
![]() $\tilde {y}_1, \tilde {y}_2\in E_1$
, then
$\tilde {y}_1, \tilde {y}_2\in E_1$
, then
and therefore
![]() $\pi _X(\tilde {y}_1)=\pi _X(\tilde {y}_2)\in \sigma ^{-1}(\{z\})$
. This means
$\pi _X(\tilde {y}_1)=\pi _X(\tilde {y}_2)\in \sigma ^{-1}(\{z\})$
. This means
![]() $\tilde {y}_1, \tilde {y}_2\in \pi _X^{-1}(\sigma ^{-1}(\{z\}))$
with
$\tilde {y}_1, \tilde {y}_2\in \pi _X^{-1}(\sigma ^{-1}(\{z\}))$
with
![]() $\sigma _{\tilde {X}}(\tilde {y}_1)=\sigma _{\tilde {X}}(\tilde {y}_2)$
. However, according to the final paragraph of Theorem 4.6 and the minimality of
$\sigma _{\tilde {X}}(\tilde {y}_1)=\sigma _{\tilde {X}}(\tilde {y}_2)$
. However, according to the final paragraph of Theorem 4.6 and the minimality of
![]() $m_z$
, the restriction of
$m_z$
, the restriction of
![]() $\sigma _{\tilde {X}}$
from
$\sigma _{\tilde {X}}$
from
![]() $\pi _X^{-1}(\sigma ^{-1}(\{z\}))$
to
$\pi _X^{-1}(\sigma ^{-1}(\{z\}))$
to
![]() $\pi _X^{-1}(\{z\})$
is injective and onto, which means that
$\pi _X^{-1}(\{z\})$
is injective and onto, which means that
![]() $\tilde {y}_1=\tilde {y}_2$
, and therefore
$\tilde {y}_1=\tilde {y}_2$
, and therefore
![]() $E_1$
is a singleton. Note that by the minimality of
$E_1$
is a singleton. Note that by the minimality of
![]() $m_z$
, we can clearly apply the same argument to the case
$m_z$
, we can clearly apply the same argument to the case
![]() $i=2,3,\ldots ,m_z$
.
$i=2,3,\ldots ,m_z$
.
For
![]() $i=m_z+1$
, from the construction in Lemma 4.4, there is a unique element corresponding to the prefix
$i=m_z+1$
, from the construction in Lemma 4.4, there is a unique element corresponding to the prefix
![]() $0$
or
$0$
or
![]() $1$
. Therefore,
$1$
. Therefore,
![]() $E_{m_z+1}$
is a singleton as well. Repeating this procedure and noting that there exists
$E_{m_z+1}$
is a singleton as well. Repeating this procedure and noting that there exists
![]() $K>0$
such that x has a unique past whenever
$K>0$
such that x has a unique past whenever
![]() $k\geq K$
and
$k\geq K$
and
![]() $x\in \sigma ^{-k}(z)$
, we conclude that
$x\in \sigma ^{-k}(z)$
, we conclude that
![]() $\tilde {z}$
has a unique past.
$\tilde {z}$
has a unique past.
On the other hand, it is quite clear that
![]() $\sigma _{\tilde {X}}$
is a surjective map restricted on
$\sigma _{\tilde {X}}$
is a surjective map restricted on
![]() $\tilde {\Lambda }_X$
, and from which we can then conclude that
$\tilde {\Lambda }_X$
, and from which we can then conclude that
![]() $\sigma _{\tilde {X}}$
is a homeomorphism from
$\sigma _{\tilde {X}}$
is a homeomorphism from
![]() $\tilde {\Lambda }_X$
onto
$\tilde {\Lambda }_X$
onto
![]() $\tilde {\Lambda }_X$
.
$\tilde {\Lambda }_X$
.
Now, we construct a map from
![]() $\underline {X}$
to
$\underline {X}$
to
![]() $\tilde {\Lambda }_X$
. This is a natural construction, which is similar to that of the Sturmian case. Specifically,
$\tilde {\Lambda }_X$
. This is a natural construction, which is similar to that of the Sturmian case. Specifically,
-
(i) If
 $x\in \underline {X}$
such that
$x\in \underline {X}$
such that
 $\sigma ^k(x_{[0,\infty )})$
has a unique past for all
$\sigma ^k(x_{[0,\infty )})$
has a unique past for all
 $k\ge 0$
, we set
$k\ge 0$
, we set  $$\begin{align*}\Phi(x)=\tilde{x}=\imath_X(x_{[0,\infty)}),\end{align*}$$
$$\begin{align*}\Phi(x)=\tilde{x}=\imath_X(x_{[0,\infty)}),\end{align*}$$
where
 $\imath _X(x_{[0,\infty )})$
is the unique element in
$\imath _X(x_{[0,\infty )})$
is the unique element in
 $\pi _X^{-1}(x_{[0,\infty )})$
by Theorem 4.7. Explicitly, for every
$\pi _X^{-1}(x_{[0,\infty )})$
by Theorem 4.7. Explicitly, for every
 $x=(x_n)_{n\in \mathbb {Z}}\in \underline {X}$
, since
$x=(x_n)_{n\in \mathbb {Z}}\in \underline {X}$
, since
 $\underline {X}$
is an inverse limit, we regard x as a sequence of right infinite words in X:
$\underline {X}$
is an inverse limit, we regard x as a sequence of right infinite words in X:  $$\begin{align*}x=\{x_{[-n,\infty)}\}_{n\ge1}.\end{align*}$$
$$\begin{align*}x=\{x_{[-n,\infty)}\}_{n\ge1}.\end{align*}$$
Then we have
 $\sigma _{\tilde {X}}\circ \Phi (x)=\sigma _{\tilde {X}}\circ \imath _X(x_{[0,\infty )})=\imath _X(x_{[1,\infty )})=\Phi \circ \sigma (x)$
.
$\sigma _{\tilde {X}}\circ \Phi (x)=\sigma _{\tilde {X}}\circ \imath _X(x_{[0,\infty )})=\imath _X(x_{[1,\infty )})=\Phi \circ \sigma (x)$
. -
(ii) If
 $x\in \underline {X}$
such that there is some
$x\in \underline {X}$
such that there is some
 $k\ge 0$
making
$k\ge 0$
making
 $\sigma ^k(x_{[0,\infty )})$
do not have a unique past, since X has property (**), we can choose
$\sigma ^k(x_{[0,\infty )})$
do not have a unique past, since X has property (**), we can choose
 $K\ge 0$
such that every element in
$K\ge 0$
such that every element in
 $\mathrm{Orb}^+_\sigma (\sigma ^K(x))$
is not left special anymore. Therefore, it is enough to determine
$\mathrm{Orb}^+_\sigma (\sigma ^K(x))$
is not left special anymore. Therefore, it is enough to determine
 $\Phi (\sigma ^K(x))$
. By abuse of notation, we denote
$\Phi (\sigma ^K(x))$
. By abuse of notation, we denote
 $\sigma ^K(x)$
by x. Let k be the smallest natural number such that
$\sigma ^K(x)$
by x. Let k be the smallest natural number such that  $$\begin{align*}x_{[-k,\infty)}\in \mathrm{Sp}_\mathrm{l}(X).\end{align*}$$
$$\begin{align*}x_{[-k,\infty)}\in \mathrm{Sp}_\mathrm{l}(X).\end{align*}$$
Then there is a unique element in
 $\pi _X^{-1}(x_{[-k,\infty )})$
corresponding to the prefix
$\pi _X^{-1}(x_{[-k,\infty )})$
corresponding to the prefix
 $x_{-k-1}\in \{0,1\}$
. Now, by applying this argument to
$x_{-k-1}\in \{0,1\}$
. Now, by applying this argument to
 $x_{[-(k+1),\infty )}$
, together with the assumption that X only has finitely many of special elements, we get a unique element
$x_{[-(k+1),\infty )}$
, together with the assumption that X only has finitely many of special elements, we get a unique element
 $\Phi (x)$
in
$\Phi (x)$
in
 $\tilde {\Lambda }_X$
. Similar to the case (i), it is straightforward to verify that
$\tilde {\Lambda }_X$
. Similar to the case (i), it is straightforward to verify that
 $\sigma _{\tilde {X}}\circ \Phi (x)=\Phi \circ \sigma (x)$
holds naturally.
$\sigma _{\tilde {X}}\circ \Phi (x)=\Phi \circ \sigma (x)$
holds naturally.
Finally, to see that
![]() $\Phi $
is a homeomorphism, we first notice that since the topology on
$\Phi $
is a homeomorphism, we first notice that since the topology on
![]() $\underline {X}$
and
$\underline {X}$
and
![]() $\tilde {\Lambda }_X$
are both generated by the cylinder sets and that
$\tilde {\Lambda }_X$
are both generated by the cylinder sets and that
![]() $\Phi $
does not change any finite prefix of any right infinite word in the sequence
$\Phi $
does not change any finite prefix of any right infinite word in the sequence
![]() $x=\{x_{[-n,\infty )}\}$
,
$x=\{x_{[-n,\infty )}\}$
,
![]() $\Phi $
is clearly continuous and injective. For the surjectivity of
$\Phi $
is clearly continuous and injective. For the surjectivity of
![]() $\Phi $
, let
$\Phi $
, let
![]() $\tilde {z}\in \tilde {\Lambda }_X$
. Since
$\tilde {z}\in \tilde {\Lambda }_X$
. Since
![]() $\tilde {z}$
has a unique past,
$\tilde {z}$
has a unique past,
![]() $\sigma _{\tilde {X}}^{-n}(\tilde {z})$
is well defined for all
$\sigma _{\tilde {X}}^{-n}(\tilde {z})$
is well defined for all
![]() $n\ge 1$
. Then define a sequence z in X by
$n\ge 1$
. Then define a sequence z in X by
Since
![]() $\sigma \circ \pi _X\circ \sigma _{\tilde {X}}^{-n-1}(\tilde {z})=\pi _X\circ \sigma _{\tilde {X}}\circ \sigma _{\tilde {X}}^{-n-1}(\tilde {z})=\pi _X\circ \sigma _{\tilde {X}}^{-n}(\tilde {z})$
, we see that z corresponds to an element in the projective system
$\sigma \circ \pi _X\circ \sigma _{\tilde {X}}^{-n-1}(\tilde {z})=\pi _X\circ \sigma _{\tilde {X}}\circ \sigma _{\tilde {X}}^{-n-1}(\tilde {z})=\pi _X\circ \sigma _{\tilde {X}}^{-n}(\tilde {z})$
, we see that z corresponds to an element in the projective system
![]() $X\stackrel {\sigma }{\leftarrow }X$
and defines a point in
$X\stackrel {\sigma }{\leftarrow }X$
and defines a point in
![]() $\underline {X}$
. From the construction above, we immediately have
$\underline {X}$
. From the construction above, we immediately have
![]() $\Phi (z)=\tilde {z}$
. This verifies the surjectivity of
$\Phi (z)=\tilde {z}$
. This verifies the surjectivity of
![]() $\Phi $
. Finally, since
$\Phi $
. Finally, since
![]() $\underline {X}$
is compact and
$\underline {X}$
is compact and
![]() $\tilde {\Lambda }_X$
is Hausdorff,
$\tilde {\Lambda }_X$
is Hausdorff,
![]() $\Phi $
is a homeomorphism.
$\Phi $
is a homeomorphism.
We now close Section 4 by summarizing in the following theorem the main results in the section.
Theorem 4.9 Let
![]() $(X,\sigma )$
be a one-sided minimal shift over
$(X,\sigma )$
be a one-sided minimal shift over
![]() $\{0,1\}$
on an infinite space X with finitely many left special elements. Let
$\{0,1\}$
on an infinite space X with finitely many left special elements. Let
![]() $\widetilde {X}$
be its cover. Then we have the following.
$\widetilde {X}$
be its cover. Then we have the following.
-
(1) The set
 $I(\widetilde {X})$
of isolated points in
$I(\widetilde {X})$
of isolated points in
 $\widetilde {X}$
is a disjoint union:
$\widetilde {X}$
is a disjoint union:  $$\begin{align*}I(\widetilde{X})=\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})),\end{align*}$$
$$\begin{align*}I(\widetilde{X})=\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}})),\end{align*}$$
which forms a dense open subset of
 $\widetilde {X}$
.
$\widetilde {X}$
. -
(2) The subsystem
 $(\widetilde {X}\setminus I(\widetilde {X}), \sigma _{\widetilde {X}}|_{\widetilde {X}\setminus I(\widetilde {X})})$
on the set of nonisolated points is invertible and conjugate to the canonical two-sided shift space
$(\widetilde {X}\setminus I(\widetilde {X}), \sigma _{\widetilde {X}}|_{\widetilde {X}\setminus I(\widetilde {X})})$
on the set of nonisolated points is invertible and conjugate to the canonical two-sided shift space
 $\underline {X}$
of X.
$\underline {X}$
of X. -
(3) For every
 $x\in X\setminus \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
,
$x\in X\setminus \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}})$
,  $$\begin{align*}\#\pi_X^{-1}(x)=1.\end{align*}$$
$$\begin{align*}\#\pi_X^{-1}(x)=1.\end{align*}$$
Moreover, for every
 $x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}}),$
$x\in \bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}}),$
 $$\begin{align*}\#\pi_X^{-1}(x)=\mathfrak{d}(x)+1,\end{align*}$$
$$\begin{align*}\#\pi_X^{-1}(x)=\mathfrak{d}(x)+1,\end{align*}$$
where
 $\mathfrak {d}(x)$
is the number of directed path in X terminating at x.
$\mathfrak {d}(x)$
is the number of directed path in X terminating at x.
Remark 4.10 Last but not least, since we only consider systems with alphabet
![]() $\mathcal {A}=\{0,1\}$
in order to simplify our proofs, we would also like to mention how our results depend on the number of symbols. In fact, all but (3) in Theorem 4.9 hold for systems over any finite alphabet
$\mathcal {A}=\{0,1\}$
in order to simplify our proofs, we would also like to mention how our results depend on the number of symbols. In fact, all but (3) in Theorem 4.9 hold for systems over any finite alphabet
![]() $\mathcal {A}$
. In fact, Lemma 4.4 may fail even for
$\mathcal {A}$
. In fact, Lemma 4.4 may fail even for
![]() $\mathcal {A}=\{0,1,2\}$
. This is because for a left special element, say
$\mathcal {A}=\{0,1,2\}$
. This is because for a left special element, say
![]() $\omega $
, we do not know exactly what is the preimage of
$\omega $
, we do not know exactly what is the preimage of
![]() $\omega $
, for it could be any of
$\omega $
, for it could be any of
![]() $\{0\omega , 1\omega \}$
,
$\{0\omega , 1\omega \}$
,
![]() $\{1\omega , 2\omega \}$
,
$\{1\omega , 2\omega \}$
,
![]() $\{0\omega ,2\omega \}$
, or
$\{0\omega ,2\omega \}$
, or
![]() $\{0\omega , 1\omega , 2\omega \}$
. On the other hand, we see that the proofs of (1) and (2) have nothing to do with the number of symbols.
$\{0\omega , 1\omega , 2\omega \}$
. On the other hand, we see that the proofs of (1) and (2) have nothing to do with the number of symbols.
5 A commutative diagram and the nuclear dimension
We conclude our main result in this short section, concerning the nuclear dimension of the Cuntz–Pimsner
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {O}_X$
associated with every minimal one-sided shift over an infinite space X with finite special elements.
$\mathcal {O}_X$
associated with every minimal one-sided shift over an infinite space X with finite special elements.
Theorem 5.1 Let X be a one-sided minimal shift space with finite special elements. Then there is a commutative diagram

where the horizontal arrows are short exact, the vertical arrows are inclusions, and
![]() $\mathfrak {n}_X$
is the number of right tail equivalence classes of left special elements in X. In addition, the Cuntz–Pimsner algebra
$\mathfrak {n}_X$
is the number of right tail equivalence classes of left special elements in X. In addition, the Cuntz–Pimsner algebra
![]() $\mathcal {O}_X$
has nuclear dimension
$\mathcal {O}_X$
has nuclear dimension
![]() $1$
.
$1$
.
Proof It suffices to show the exact sequence on the second row, since
![]() $c_0^{\mathfrak {n}_X}$
corresponds to the abelian
$c_0^{\mathfrak {n}_X}$
corresponds to the abelian
![]() $C^*$
-algebra of the space of
$C^*$
-algebra of the space of
![]() $\mathfrak {n}_X$
discrete orbits and the commutativity of the diagram is induced by
$\mathfrak {n}_X$
discrete orbits and the commutativity of the diagram is induced by
![]() $\pi _X$
. From the description of the cover
$\pi _X$
. From the description of the cover
![]() $\widetilde {X}$
, the unit space of its groupoid
$\widetilde {X}$
, the unit space of its groupoid
![]() $\mathcal {G}_{\widetilde {X}}$
decomposes into two parts:
$\mathcal {G}_{\widetilde {X}}$
decomposes into two parts:
 $$\begin{align*}\mathcal{G}_{\widetilde{X}}^0=\tilde{\Lambda}_X\bigsqcup\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath_X(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}}))\right).\end{align*}$$
$$\begin{align*}\mathcal{G}_{\widetilde{X}}^0=\tilde{\Lambda}_X\bigsqcup\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath_X(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}}))\right).\end{align*}$$
In particular, the groupoid restricted to
![]() $\tilde {\Lambda }_X$
is isomorphic to
$\tilde {\Lambda }_X$
is isomorphic to
![]() $\underline {X}\rtimes _\sigma \mathbb {Z}$
by Theorem 4.8, whose
$\underline {X}\rtimes _\sigma \mathbb {Z}$
by Theorem 4.8, whose
![]() $C^*$
-algebra is
$C^*$
-algebra is
![]() $*$
-isomorphic to the crossed product
$*$
-isomorphic to the crossed product
![]() $C(\underline {X})\rtimes _\sigma \mathbb {Z}$
, and the groupoid restricted to the open subset
$C(\underline {X})\rtimes _\sigma \mathbb {Z}$
, and the groupoid restricted to the open subset
![]() $\bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\imath _X(\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}}))$
is the sum of full equivalence relations restricted on each discrete orbit
$\bigsqcup _{\mathfrak {j}\in \mathcal {J}_X}\imath _X(\mathrm{Orb}_{\sigma }(\omega _{\mathfrak {j}}))$
is the sum of full equivalence relations restricted on each discrete orbit
![]() $\imath _X(\mathrm{Orb}_\sigma (\omega _{\mathfrak {j}}))\,(\mathfrak {j}\in \mathcal {J}_X)$
, whose
$\imath _X(\mathrm{Orb}_\sigma (\omega _{\mathfrak {j}}))\,(\mathfrak {j}\in \mathcal {J}_X)$
, whose
![]() $C^*$
-algebra is
$C^*$
-algebra is
![]() $*$
-isomorphic to the direct sum
$*$
-isomorphic to the direct sum
![]() $\mathbb {K}^{\mathfrak {n}_X}$
. Then the exactness of the second row follows from Proposition 4.3.2 in [Reference Sims and Williams20].
$\mathbb {K}^{\mathfrak {n}_X}$
. Then the exactness of the second row follows from Proposition 4.3.2 in [Reference Sims and Williams20].
For the nuclear dimension of
![]() $\mathcal {O}_X$
, we first claim that
$\mathcal {O}_X$
, we first claim that
To see this, let K be an open relative compact subset of
![]() $\mathcal {G}_{\widetilde {X}}$
. Denote the groupoid restricted on
$\mathcal {G}_{\widetilde {X}}$
. Denote the groupoid restricted on
![]() $\tilde {\Lambda }_X=\underline {X}$
by
$\tilde {\Lambda }_X=\underline {X}$
by
![]() $\mathcal {G}_{\tilde {\Lambda }}$
. It has already been verified that
$\mathcal {G}_{\tilde {\Lambda }}$
. It has already been verified that
![]() $\mathcal {G}_{\tilde {\Lambda }}$
is a minimal reversible groupoid, or in other words, a groupoid of an invertible minimal action on an infinite compact space, which follows that it has asymptotic dimension
$\mathcal {G}_{\tilde {\Lambda }}$
is a minimal reversible groupoid, or in other words, a groupoid of an invertible minimal action on an infinite compact space, which follows that it has asymptotic dimension
![]() $1$
. Then there are open subsets
$1$
. Then there are open subsets
![]() $\tilde {U}_0, \tilde {U}_1$
of its unit space
$\tilde {U}_0, \tilde {U}_1$
of its unit space
![]() $\mathcal {G}_{\tilde {\Lambda }}^0$
that cover
$\mathcal {G}_{\tilde {\Lambda }}^0$
that cover
![]() $s(K\cap \mathcal {G}_{\tilde {\Lambda }})\cup r(K\cap \mathcal {G}_{\tilde {\Lambda }})$
, and the set
$s(K\cap \mathcal {G}_{\tilde {\Lambda }})\cup r(K\cap \mathcal {G}_{\tilde {\Lambda }})$
, and the set
is contained in a relatively compact subgroupoid of
![]() $\mathcal {G}_{\tilde {\Lambda }}$
for
$\mathcal {G}_{\tilde {\Lambda }}$
for
![]() $i=0,1$
. Let
$i=0,1$
. Let
 $$\begin{align*}U_i=\tilde{U}_i\sqcup\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath_X(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}}))\right).\end{align*}$$
$$\begin{align*}U_i=\tilde{U}_i\sqcup\left(\bigsqcup_{\mathfrak{j}\in\mathcal{J}_X}\imath_X(\mathrm{Orb}_{\sigma}(\omega_{\mathfrak{j}}))\right).\end{align*}$$
It is clear that
![]() $U_i$
are open and cover
$U_i$
are open and cover
![]() $s(K)\cup r(K)$
. On the other hand, since the rightmost one is a discrete open set and K is relatively compact, the set
$s(K)\cup r(K)$
. On the other hand, since the rightmost one is a discrete open set and K is relatively compact, the set
![]() $\{g\in K\setminus \mathcal {G}_{\tilde {\Lambda }}: s(g), r(g)\in U_i\}$
is a finite set for
$\{g\in K\setminus \mathcal {G}_{\tilde {\Lambda }}: s(g), r(g)\in U_i\}$
is a finite set for
![]() $i=0,1$
. This implies that the groupoid generated by
$i=0,1$
. This implies that the groupoid generated by
is a relatively compact subgroupoid for
![]() $i=0,1$
. This shows that
$i=0,1$
. This shows that
![]() $\mathcal {G}_{\widetilde {X}}$
has dynamic asymptotic dimension
$\mathcal {G}_{\widetilde {X}}$
has dynamic asymptotic dimension
![]() $1$
.
$1$
.
Now, from Theorem 8.6 of [Reference Guentner, Willett and Yu12],
However, by the exact sequence and Proposition 2.9 of [Reference Williams21],
 $$ \begin{align*} 1&=\max\{\mathrm{dim}_{\mathrm{nuc}}(\mathbb{K}^{\mathfrak{n}_X}), \mathrm{dim}_{\mathrm{nuc}}(C(\underline{X})\rtimes_{\sigma}\mathbb{Z})\}\\ &\leq\mathrm{dim}_{\mathrm{nuc}}(\mathcal{O}_X)\\ &\leq\mathrm{dim}_{\mathrm{nuc}}(\mathbb{K}^{\mathfrak{n}_X})+\mathrm{dim}_{\mathrm{nuc}}(C(\underline{X})\rtimes_{\sigma}\mathbb{Z})+1=2. \end{align*} $$
$$ \begin{align*} 1&=\max\{\mathrm{dim}_{\mathrm{nuc}}(\mathbb{K}^{\mathfrak{n}_X}), \mathrm{dim}_{\mathrm{nuc}}(C(\underline{X})\rtimes_{\sigma}\mathbb{Z})\}\\ &\leq\mathrm{dim}_{\mathrm{nuc}}(\mathcal{O}_X)\\ &\leq\mathrm{dim}_{\mathrm{nuc}}(\mathbb{K}^{\mathfrak{n}_X})+\mathrm{dim}_{\mathrm{nuc}}(C(\underline{X})\rtimes_{\sigma}\mathbb{Z})+1=2. \end{align*} $$
We then conclude that
![]() $\mathrm {dim}_{\mathrm {nuc}}(\mathcal {O}_X)=1$
. This finishes the proof.
$\mathrm {dim}_{\mathrm {nuc}}(\mathcal {O}_X)=1$
. This finishes the proof.
Remark 5.2 An alternative argument for the last part of Theorem 5.1 would just be that, as a
![]() $C^*$
-algebra of a groupoid associated with a minimal system over an infinite compact metric space,
$C^*$
-algebra of a groupoid associated with a minimal system over an infinite compact metric space,
![]() $\mathcal {O}_X$
is not approximately finite-dimensional. This follows immediately that
$\mathcal {O}_X$
is not approximately finite-dimensional. This follows immediately that
![]() $\mathrm {dim}_{\mathrm {nuc}}(\mathcal {O}_X)\ge 1$
.
$\mathrm {dim}_{\mathrm {nuc}}(\mathcal {O}_X)\ge 1$
.
Acknowledgment
We would like to thank members of the Research Center for Operator Algebras for providing online discussions weekly during the difficult period of COVID-19. The second named author would also like to thank his advisor Huaxin Lin from whom he is learning a lot as a doctoral student. The authors thank the anonymous referee for many helpful comments and suggestions as well.