Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-30T15:22:13.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal, Locally Compact, Boundedly Metacompact Spaces are Paracompact: an Application of Pixley-Roy Spaces

Published online by Cambridge University Press:  20 November 2018

Peg Daniels
Peg Daniels*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let PR(X) denote the Pixley-Roy topology on the collection of all nonempty, finite subsets of a space X. For each cardinal κ, let κ* be the cardinal κ with the co-finite topology. We use PR(κ*) to obtain a partial solution in ZFC to F. Tall's question whether every normal, locally compact, metacompact space is paracompact [6]. W.S. Watson has answered this question affirmatively assuming V = L[7]. The question also has an affirmative answer if we assume either that the space is perfectly normal [1] or that it is locally connected [4].

A space X is said to be boundedly metacompact (boundedly paracompact) provided that for each open cover 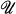of X there is a positive integer n such that 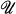has a point finite (locally finite) open refinement of order n. As the main result of this paper, we show every normal, locally compact, boundedly metacompact space is paracompact.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 807 - 823
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. A.V., Arhangel'skii, The property of paracompactness in the class of perfectly normal, locally hicompact spaces, Soviet Math. Dokl. 12 (1971), 1253–1257.Google Scholar
2. E.K., van Douwen, The Pixley-Roy topology on spaces of subsets, Set Theoretic Topology (Academic Press, Inc., New York, 1977), 111–134.Google Scholar
3. P., Fletcher, R.A., McCoy and R., Slover, On boundedly metacompact and boundedly paracompact spaces, Proceedings of the American Mathematical Society 25 (1970), 335–342.Google Scholar
4. G., Gruenhage, Paracompactness in normal, locally connected, locally compact spaces, Topology Proc. 4 (1979), 393–405.Google Scholar
5. T., Jech, Set theory (Academic Press, Inc., New York, 1978), exercise 7.9.Google Scholar
6. F., Tall, On the existence of normal metacompact Moore spaces which are not metrizable, Can. J. Math. 26 (1974), 1–6.Google Scholar
7. W.S., Watson, Locally compact normal spaces in the constructible universe, to appear in Can. J. Math.Google Scholar
8. J.M., Worrell, Jr., The closed images of metacompact topological spaces, Portugal Math. 25 (1966), 175–179.Google Scholar