Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T07:55:22.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Backtracking Random Walks and Cogrowth of Graphs

Published online by Cambridge University Press:  20 November 2018

Ronald Ortner  and
Wolfgang Woess
Ronald Ortner
Affiliation:
Department Mathematik und Informationstechnolgie, Montanuniversität Leoben, Franz-Josef-Strasse 18, A-8700 Leoben, Austria email: [email protected]
Wolfgang Woess
Affiliation:
Institut für Mathematische Strukturtheorie, Technische Universität Graz, Steyrergasse 30, A-8010 Graz, Austria email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

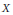Let $X$ be a locally finite, connected graph without vertices of degree 1. Non-backtracking random walk moves at each step with equal probability to one of the “forward” neighbours of the actual state, i.e., it does not go back along the preceding edge to the preceding state. This is not a Markov chain, but can be turned into a Markov chain whose state space is the set of oriented edges of 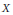$X$. Thus we obtain for infinite 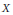$X$ that the $n$-step non-backtracking transition probabilities tend to zero, and we can also compute their limit when 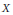$X$ is finite. This provides a short proof of an old result concerning cogrowth of groups, and makes the extension of that result to arbitrary regular graphs rigorous. Even when 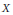$X$ is non-regular, but small cycles are dense in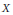$X$, we show that the graph 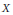$X$ is non-amenable if and only if the non-backtracking $n$-step transition probabilities decay exponentially fast. This is a partial generalization of the cogrowth criterion for regular graphs which comprises the original cogrowth criterion for finitely generated groups of Grigorchuk and Cohen.

Keywords

05C7560G5020F69graphoriented line graphcovering treerandom walkcogrowthamenability
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 828 - 844
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bartholdi, L., Counting paths in graphs. Enseign. Math. (2) 45(1999), no. 1-2, 83–131.Google Scholar
[2] Chung, K. L., Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin, 1960.Google Scholar
[3] Cohen, J. M., Cogrowth and amenability of discrete groups. J. Funct. Anal. 48(1982), no. 3, 301–309.Google Scholar
[4] Dodziuk, J., Difference equations, isoperimetric inequality, and transience of certain random walks. Trans. Amer. Math. Soc. 284(1984), no. 2, 787–794.Google Scholar
[5] Dodziuk, J. and Kendall, W. S., Combinatorial Laplacians and isoperimetric inequality. In: From Local Times to Global Geometry, Control and Physics, Pitman Res. Notes Math. Ser. 150, Longman Sci. Tech., Harlow, 1986, pp. 68–74.Google Scholar
[6] Grigorchuk, R. I., Symmetric random walks on discrete groups. In: Multicomponent Random Systems Adv. Probab. Related Topics 6, Dekker, New York 1980, pp. 285–325.Google Scholar
[7] Guivarc’h, Y., Sur la loi des grands nombres et le rayon spectral d’une marche aléatoire, Astérisque 74, Soc. Math. France, Paris, 1980, pp. 47–98.Google Scholar
[8] de la Harpe, P., Topics in Geometric Group Theory, Chicago Lectures in Mathematics, University of Chicago Press, Chicago, IL, 2000.Google Scholar
[9] Kapovich, I., Myasnikov, A., Schupp, P., and Shpilrain, V., Generic-case complexity, decision problems in group theory and random walks. J. Algebra 264(2003), no. 2, 665–694.Google Scholar
[10] Kesten, H., Full Banach mean values on countable groups. Math. Scand. 7(1959), 146–156.Google Scholar
[11] Northshield, S., Cogrowth of regular graphs. Proc. Amer. Math. Soc. 116(1992), no. 1, 203–205.Google Scholar
[12] Northshield, S., Quasi-regular graphs, cogrowth, and amenability. Discrete Contin. Dyn. Syst. suppl(2003), 678–687.Google Scholar
[13] Northshield, S., Cogrowth of arbitrary graphs. In: Random Walks and Geometry, de Gruyter, Berlin 2004, pp. 501–513.Google Scholar
[14] Seneta, E., Non-Negative Matrices and Markov Chains. Springer, Berlin, 1973.Google Scholar
[15] R., Szwarc: A short proof of the Grigorchuk-Cohen cogrowth theorem. Proc. Amer. Math. Soc. 106(1989), no. 3, 663–665.Google Scholar
[16] Woess, W., Cogrowth of groups and simple random walks. Arch. Math. (Basel) 41(1983), no. 4, 363–370.Google Scholar
[17] Woess, W., RandomWalks on Infinite Graphs and Groups. Cambridge Tracts in Mathematics 138, Cambridge University Press, Cambridge, 2000.Google Scholar