Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T12:39:27.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Negative Powers of Laguerre Operators

Published online by Cambridge University Press:  20 November 2018

Adam Nowak  and
Krzysztof Stempak
Adam Nowak
Affiliation:
Instytut Matematyczny, Polska Akademia Nauk, Śniadeckich 8, 00—956 Warszawa, Poland and Instytut Matematyki i Informatyki, Politechnika Wrocławska, 50—370 Wrocław, Poland email: [email protected]
Krzysztof Stempak
Affiliation:
Instytut Matematyki i Informatyki, Politechnika Wrocławska, 50—370 Wrocław, Poland email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

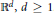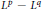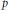We study negative powers of Laguerre differential operators in ${{\mathbb{R}}^{d}},\,d\,\ge \,1$. For these operators we prove two-weight $[{{L}^{p}}\,-\,{{L}^{q}}$ estimates with ranges of $q$ depending on $p$. The case of the harmonic oscillator (Hermite operator) has recently been treated by Bongioanni and Torrea by using a straightforward approach of kernel estimates. Here these results are applied in certain Laguerre settings. The procedure is fairly direct for Laguerre function expansions of Hermite type, due to some monotonicity properties of the kernels involved. The case of Laguerre function expansions of convolution type is less straightforward. For half-integer type indices. we transfer the desired results from the Hermite setting and then apply an interpolation argument based on a device we call the convexity principle to cover the continuous range of 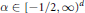$\alpha \,\in \,\,{{[-1/2,\infty )}^{d}}$. Finally, we investigate negative powers of the Dunkl harmonic oscillator in the context of a finite reflection group acting on 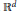${{\mathbb{R}}^{d}}$ and isomorphic to 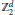$\mathbb{Z}_{2}^{d}$. The two weight 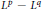${{L}^{p}}\,-\,{{L}^{q}}$ estimates we obtain in this setting are essentially consequences of those for Laguerre function expansions of convolution type.

Keywords

47G4031C1526A33potential operatorfractional integralRiesz potentialnegative powerharmonic oscillatorLaguerre operatorDunkl harmonic oscillator
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 1 , 01 February 2012 , pp. 183 - 216
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Aronszajn, N. and Smith, K. T., Theory of Bessel potentials. I. Ann. Inst. Fourier (Grenoble) 11(1961), 385-475.Google Scholar
[2] Bongioanni, B. and Torrea, J. L., Sobolev spaces associated to the harmonic oscillator. Proc. Indian Acad. Sci. Math. Sci. 116(2006), 337-360. http://dx. doi. org/10.1007/BF02829750Google Scholar
[3] Luca, F. and Shparlinski, I. E., What is a Sobolev space for the Laguerre function systems? Studia Math. 192(2009), no. 2, 147-172. http://dx. doi. org/10.4064/sm192-2-4Google Scholar
[4] Bongioanni, B., Harboure, E., and Salinas, O., Weighted inequalities for negative powers of Schrödinger operators. J. Math. Anal. Appl. 348(2008), no. 1, 12-27. http://dx. doi. org/10.1016/j. jmaa.2008.06.045Google Scholar
[5] De Nápoli, P., Drelichman, I., Durán, R., Multipliers of Laplace transform type for Laguerre and Hermite expansions. Studia Math. 203(2011), no. 3, 265-290.Google Scholar
[6] Długosz, J., Lp-multipliers for the Laguerre expansions. Colloq. Math. 54(1987), no. 2, 285-293.Google Scholar
[7] Duoandikoetxea, J., Fourier analysis. Graduate Studies in Mathematics, 29, American Mathematical Society, Providence, RI, 2001.Google Scholar
[8] Duong, X. T., Ouhabaz, E. M., and Sikora, A., Plancherel-type estimates and sharp spectral multipliers. J. Funct. Anal. 196(2002), no. 2, 443-485. http://dx. doi. org/10.1016/S0022-1236(02)00009-5Google Scholar
[9] Gasper, G., Stempak, K., and Trebels, W., Fractional integration for Laguerre expansions. Methods Appl. Anal. 2(1995), no. 1, 67-75.Google Scholar
[10] Gasper, G. and W. Trebels, Norm inequalities for fractional integrals of Laguerre and Hermite expansions. Tohoku Math. J. 52(2000), no. 2, 251-260. http://dx. doi. org/10.2748/tmj/1178224609Google Scholar
[11] Gutiérrez, C. E., Incognito, A., and Torrea, J. L., Riesz transforms, g-functions, and multipliers for the Laguerre semigroup. Houston J. Math. 27(2001), no. 3, 579-592.Google Scholar
[12] Hörmander, L., Estimates for translation invariant operators in Lp spaces. Acta Math. 104(1960), 94-140. http://dx. doi. org/10.1007/BF02547187Google Scholar
[13] Kanjin, Y., A transplantation theorem for Laguerre series. Tohoku Math. J. 43(1991), no. 4, 537-555. http://dx. doi. org/10.2748/tmj/1178227427Google Scholar
[14] Kanjin, Y. and Sato, E., The Hardy-Littlewood theorem on fractional integration for Laguerre series. Proc. Amer. Math. Soc. 123(1995), no. 7, 2165-2171. http://dx. doi. org/10.1090/S0002-9939-1995-1257113-2Google Scholar
[15] Kerman, R. A., Convolution theorems with weights. Trans. Amer. Math. Soc. 280(1983), no. 1, 207-219. http://dx. doi. org/10.1090/S0002-9947-1983-0712256-0Google Scholar
[16] Lebedev, N. N., Special functions and their applications. Revised Edition, Dover Publications, Inc., New York, 1972.Google Scholar
[17] Muckenhoupt, B. and Stein, E. M., Classical expansions and their relation to conjugate harmonic functions. Trans. Amer. Math. Soc. 118(1965), 17-92. http://dx. doi. org/10.1090/S0002-9947-1965-0199636-9Google Scholar
[18] Nowak, A. and Stempak, K., Riesz transforms and conjugacy for Laguerre function expansions of Hermite type. J. Funct. Anal. 244(2007), no. 2, 399-443. http://dx. doi. org/10.1016/j. jfa.2006.12.010Google Scholar
[19] Luca, F. and Shparlinski, I. E., Riesz transforms for multi-dimensional Laguerre function expansions. Adv. Math. 215(2007), no. 2, 642-678. http://dx. doi. org/10.1016/j. aim.2007.04.010Google Scholar
[20] Luca, F. and Shparlinski, I. E., Riesz transforms for the Dunkl harmonic oscillator. Math. Z. 262(2009), no. 3, 539-556. http://dx. doi. org/10.1007/s00209-008-0388-4Google Scholar
[21] Luca, F. and Shparlinski, I. E., Imaginary powers of the Dunkl harmonic oscillator. SIGMA Symmetry, Integrability Geom. Methods Appl, 5(2009), 016, 12 pp.Google Scholar
[22] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[23] Stein, E. M., Topics in harmonic analysis related to Littlewood-Paley theory. Annals of Mathematics Studies, 63, Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, 1970.Google Scholar
[24] Stein, E. M. and Weiss, G., Fractional integrals on n-dimensional Euclidean space. J. Math. Mech. 7(1958), 503-514.Google Scholar
[25] Stempak, K. and Torrea, J. L., Poisson integrals and Riesz transforms for Hermite function expansions with weights. J. Funct. Anal. 202(2003), no. 2, 443-472. http://dx. doi. org/10.1016/S0022-1236(03)00083-1Google Scholar
[26] Stempak, K. and Torrea, J. L., BMO results for operators associated to Hermite expansions. Illinois J. Math. 49(2005), no. 4, 1111-1131.Google Scholar
[27] Stempak, K. andW. Trebels, On weighted transplantation and multipliers for Laguerre expansions. Math. Ann. 300(1994), no. 2, 203-219. http://dx. doi. org/10.1007/BF01450484Google Scholar
[28] Thangavelu, S., Lectures on Hermite and Laguerre expansions. Mathematical Notes, 42, Princeton University Press, Princeton, NJ, 1993.Google Scholar