Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Buckley, Stephen M.
Ramanujan, M. S.
and
Vukotić, Dragan
1999.
Bounded and compact multipliers between Bergman and Hardy spaces.
Integral Equations and Operator Theory,
Vol. 35,
Issue. 1,
p.
1.
Wojtaszczyk, P.
2003.
Vol. 2,
Issue. ,
p.
1671.
Shamoyan, R. F.
2005.
On coefficient multipliers in the spaces BMOA.
Mathematical Notes,
Vol. 77,
Issue. 3-4,
p.
580.
Шамоян, Роми Файзоевич
and
Shamoyan, Romi Faizoevich
2005.
О коэффициентных мультипликаторах пространств BMOA.
Математические заметки,
Vol. 77,
Issue. 4,
p.
630.
Jevtić, Miroljub
and
Pavlović, Miroslav
2006.
On the solid hull of the Hardy space Hp, 0 < p < 1.
Michigan Mathematical Journal,
Vol. 54,
Issue. 2,
Shi, Jihuai
and
Ren, Guangbin
2006.
Coefficient multipliers of mixed norm space in the ball.
Science in China Series A: Mathematics,
Vol. 49,
Issue. 11,
p.
1491.
Blasco, Oscar
2008.
Norm estimates for operators from Hp to ℓq.
Journal of Mathematical Analysis and Applications,
Vol. 344,
Issue. 1,
p.
449.
Lengfield, Marc
2008.
A Nested Embedding Theorem for Hardy-Lorentz Spaces with Applications to Coefficient Multiplier Problems.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 4,
Blasco, Oscar
and
Pérez-Esteva, Salvador
2011.
Schatten-Herz Operators, Berezin Transform and Mixed Norm Spaces.
Integral Equations and Operator Theory,
Vol. 71,
Issue. 1,
p.
65.
Kwessi, E.
De Souza, G.
Abebe, A.
and
Aulaskari, R.
2013.
Characterization of lacunary functions in weighted Bergman–Besov–Lipschitz spaces.
Complex Variables and Elliptic Equations,
Vol. 58,
Issue. 2,
p.
157.
Naik, Sunanda
and
Rajbangshi, Karabi
2014.
Multipliers on H(p, q, α) spaces.
Arabian Journal of Mathematics,
Vol. 3,
Issue. 3,
p.
349.
Eikrem, Kjersti Solberg
and
Malinnikova, Eugenia
2015.
Coefficients Multipliers of Weighted Spaces of Harmonic Functions.
Integral Equations and Operator Theory,
Vol. 82,
Issue. 4,
p.
555.
Arévalo, Irina
2015.
A characterization of the inclusions between mixed norm spaces.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
942.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
247.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
237.
Naik, S.
and
Rajbangshi, K.
2017.
Coefficient multipliers on mixed-norm spaces
$$H(p,q,\varphi )$$
H
(
p
,
q
,
φ
)
.
The Journal of Analysis,
Vol. 25,
Issue. 1,
p.
29.
Arévalo, Irina
Contreras, Manuel D.
and
Rodríguez-Piazza, Luis
2019.
Semigroups of composition operators and integral operators on mixed norm spaces.
Revista Matemática Complutense,
Vol. 32,
Issue. 3,
p.
767.
Karapetyants, Alexey
and
Samko, Stefan
2020.
Hadamard–Bergman Convolution Operators.
Complex Analysis and Operator Theory,
Vol. 14,
Issue. 8,
Domínguez, Salvador
and
Girela, Daniel
2021.
Superposition operators between mixed norm spaces of analytic functions.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 1,
Llinares, Adrián
and
Vukotić, Dragan
2022.
Contractive inequalities for mixed norm spaces and the Beta function.
Journal of Mathematical Analysis and Applications,
Vol. 509,
Issue. 1,
p.
125938.


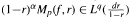 . As corollaries we recover some new results about multipliers on Bergman spaces and Hardy spaces.
. As corollaries we recover some new results about multipliers on Bergman spaces and Hardy spaces.