Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chung, Kiryong
and
Moon, Han-Bom
2017.
Mori's Program for the Moduli Space of Conics in
Grassmannian.
Taiwanese Journal of Mathematics,
Vol. 21,
Issue. 3,
Blankers, Vance
2022.
Extremality of rational tails boundary strata in $$\pmb {{\overline{\mathscr {M}}}_{g,n}}$$.
European Journal of Mathematics,
Vol. 8,
Issue. 2,
p.
523.
Schock, Nolan
2024.
The W(E6)$W(E_6)$‐invariant birational geometry of the moduli space of marked cubic surfaces.
Mathematische Nachrichten,
Vol. 297,
Issue. 7,
p.
2639.


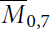 with Symmetric Divisors
with Symmetric Divisors