Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heerema, Nickolas
and
Tucker, David
1975.
Modular field extensions.
Proceedings of the American Mathematical Society,
Vol. 53,
Issue. 2,
p.
301.
Deveney, James Kevin
1976.
A counterexample concerning inseparable field extensions.
Proceedings of the American Mathematical Society,
Vol. 55,
Issue. 1,
p.
33.
Deveney, James K.
and
Mordeson, John N.
1977.
Invariants of reliable field extensions.
Archiv der Mathematik,
Vol. 29,
Issue. 1,
p.
141.
Deveney, James K.
and
Mordeson, John N.
1979.
Pencils of higher derivations of arbitrary field extensions.
Proceedings of the American Mathematical Society,
Vol. 74,
Issue. 2,
p.
205.
Mordeson, John N.
1981.
Modular extensions and abelian groups.
Archiv der Mathematik,
Vol. 36,
Issue. 1,
p.
13.
1989.
Topics in Field Theory.
Vol. 155,
Issue. ,
p.
477.
Sato, Shizuka
1990.
On modular extensions.
Proceedings of the American Mathematical Society,
Vol. 109,
Issue. 3,
p.
621.
Deveney, James K.
and
Mordeson, John N.
1996.
Vol. 1,
Issue. ,
p.
187.


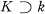 be fields of characteristic
be fields of characteristic 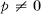 .
. 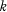 if
if 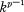 are linearly disjoint over
are linearly disjoint over 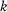 .
. 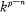 are linearly disjoint over their intersection for all
are linearly disjoint over their intersection for all 