No CrossRef data available.
Article contents
The Maximum Term and the Rank of an Entire Function
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
1. For an entire function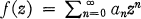 
, let M(r, f), μ(r, f), and v(r, f) denote the maximum modulus, the maximum term, and the rank for |z\ = r, respectively. Also, let
and λ(r) the lower proximate order relative to log M(r, f). For the properties of the lower proximate order, we refer the reader to the paper by Shah (1).
2. We prove the following theorems.
THEOREM 1. For an entire function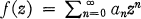
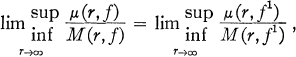
where μ(r, f1) and M(r, f1) correspond to fl(z), the derivative of f(z), provided (n + l)Rn > nRn+1, when L(f) > 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
References
1.
Shah, S. M., A note on lower proximate orders, J. Indian Math. Soc. (N.S.)
12 (1948), 31–32.Google Scholar
2.
Valiron, G., Lectures on the general theory of integral functions, Translated by Collingwood, E. F. (Imprimerie et Librairie, Edouere Privât, Toulouse, 1923).Google Scholar
A correction has been issued for this article:
You have
Access
Linked content
Please note a has been issued for this article.