Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T15:44:11.877Z Has data issue: false hasContentIssue false
  • English
  • Français

λ-Mappings Between Representation Rings of Lie Algebras

Published online by Cambridge University Press:  20 November 2018

R. V. Moody  and
A. Pianzola
R. V. Moody
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
A. Pianzola
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [10] Patera and Sharp conceived a new relation, subjoining, between semisimple Lie algebras. Our objective in this paper is twofold. Firstly, to lay down a mathematical formalization of this concept for arbitrary Lie algebras. Secondly, to give a complete classification of all maximal subjoinings between Lie algebras of the same rank, of which many examples were already known to the above authors.

The notion of subjoining is a generalization of the subalgebra relation between Lie algebras. To give an intuitive idea of what is involved we take a simple example. Suppose 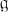is a complex simple Lie algebra of type B2. Let 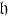be a Cartan subalgebra of 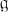and Δ the corresponding root system. We have the standard root diagram

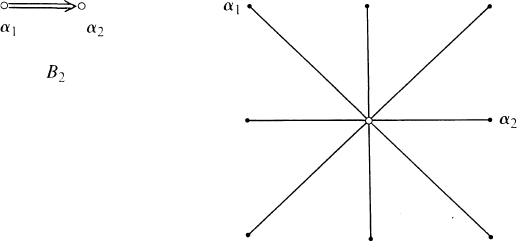
Inside B2 there lies the subalgebra A1 × A1 which can be identified with the sum of and the root spaces corresponding to the long roots of B2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 898 - 960
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. A., Borel and J., de Siebenthal, Les sous-groupes fermés de rang maximum des groupes de Lie clos, Comment. Math. Helv. 23 (1949), 200–221.Google Scholar
2. N., Bourbaki, Commutative algebra (Addison-Wesley, 1972).Google Scholar
3. N., Bourbaki, Groupes et algèbres de Lie, Ch. 4, 5, 6 (Hermann, Paris, 1968).Google Scholar
4. N., Bourbaki, Groupes et algèbres de Lie, Ch. 7, 8 (Hermann, Paris, 1975).Google Scholar
5. A., Grothendieck, La théorie des classes de Chern, Bull. Soc. Math. France 86 (1958), 137–154.Google Scholar
6. R. C., King, Unitary group subjoining, J. Phys. A:Math. Gen. 13 (1980).Google Scholar
7. D., Knutson, X-rings and the representation of the unitary group, Lecture Notes in Mathematics 308 (Springer-Verlag).Google Scholar
8. S., Lang, Algebraic number theory (Addison-Wesley, 1970).Google Scholar
9. R. V., Moody, Lie algebra subjoining, C. R. Math. Rep. Acad. Sci. Canada 5 (1980), 259–264.Google Scholar
10. J., Patera and R., Sharp, Generating functions for plethysms of finite and continuous groups, J. Phys. A:Math. Gen. 13 (1980), 397–416.Google Scholar
11. J., Patera, R., Sharp and R., Slansky, On a new relation between semi-simple Lie algebras, J. Math. Phys. 21 (1980), 2335.Google Scholar
12. A., Pianzola, Isomorphically representable Lie algebras, (Thesis), University of Saskatchewan, (1981).Google Scholar
13. J. F., Adams and Z., Mahmud, Maps between classifying spaces, Inventiones Math. 35 (1976), 1–41.Google Scholar
14. J. F., Adams, Maps between classifying spaces. II, Inventiones Math. 49 (1978), 1–65.Google Scholar
15. E. M., Friedlander, Exceptional isogenics and the classifying spaces of simple Lie groups, Ann. Math 101 (1975), 510–520.Google Scholar