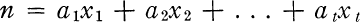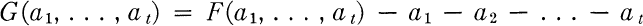Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heap, B. R.
and
Lynn, M. S.
1964.
A graph-theoretic algorithm for the solution of a linear diophantine problem of frobenius.
Numerische Mathematik,
Vol. 6,
Issue. 1,
p.
346.
Byrnes, J.S
1974.
On a partition problem of Frobenius.
Journal of Combinatorial Theory, Series A,
Vol. 17,
Issue. 2,
p.
162.
Brenowitz, Michael
Bonaventura, Celia
Bonaventura, Joseph
and
Gianazza, Elisabetta
1981.
Subunit composition of a high molecular weight oligomer: Limulus polyphemus hemocyanin.
Archives of Biochemistry and Biophysics,
Vol. 210,
Issue. 2,
p.
748.
Incerpi, Janet
and
Sedgewick, Robert
1983.
Improved upper bounds on shellsort.
p.
48.
Jia-yu, Shao
1985.
On a conjecture about the exponent set of primitive matrices.
Linear Algebra and its Applications,
Vol. 65,
Issue. ,
p.
91.
Incerpi, Janet
and
Sedgewick, Robert
1985.
Improved upper bounds on shellsort.
Journal of Computer and System Sciences,
Vol. 31,
Issue. 2,
p.
210.
Sedgewick, Robert
1986.
A new upper bound for Shellsort.
Journal of Algorithms,
Vol. 7,
Issue. 2,
p.
159.
Fröberg, R.
Gottlieb, C.
and
Häggkvist, R.
1986.
On numerical semigroups.
Semigroup Forum,
Vol. 35,
Issue. 1,
p.
63.
Greenberg, Harold
1988.
Solution to a linear diophantine equation for nonnegative integers.
Journal of Algorithms,
Vol. 9,
Issue. 3,
p.
343.
Weiss, Mark Allen
and
Sedgewick, Robert
1988.
SWAT 88.
Vol. 318,
Issue. ,
p.
255.
Weiss, Mark Allen
and
Sedgewick, Robert
1990.
More on shellsort increment sequences.
Information Processing Letters,
Vol. 34,
Issue. 5,
p.
267.
Weiss, Mark Allen
and
Sedgewick, Robert
1990.
Tight lower bounds for Shellsort.
Journal of Algorithms,
Vol. 11,
Issue. 2,
p.
242.
Pröberg, Ralf
1994.
The frobenius number of some semigroups.
Communications in Algebra,
Vol. 22,
Issue. 14,
p.
6021.
Sedgewick, Robert
1996.
Algorithms — ESA '96.
Vol. 1136,
Issue. ,
p.
1.
Кан, Игорь Давидович
Kan, Igor' Davidovich
Стечкин, Борис Сергеевич
Stechkin, Boris Sergeevich
Шарков, И В
and
Sharkov, I V
1997.
К проблеме Фробениуса трех аргументов.
Математические заметки,
Vol. 62,
Issue. 4,
p.
626.
Kan, I. D.
Stechkin, B. S.
and
Sharkov, I. V.
1997.
Frobenius problem for three arguments.
Mathematical Notes,
Vol. 62,
Issue. 4,
p.
521.
Kan, I. D.
2000.
Representation of numbers by linear forms.
Mathematical Notes,
Vol. 68,
Issue. 2,
p.
185.
Кан, Игорь Давидович
and
Kan, Igor' Davidovich
2000.
Представление чисел линейными формами.
Математические заметки,
Vol. 68,
Issue. 2,
p.
210.
Кан, Игорь Давидович
and
Kan, Igor' Davidovich
2001.
Проблема Фробениуса для классов полиномиальной разрешимости.
Математические заметки,
Vol. 70,
Issue. 6,
p.
845.
Beck, Matthias
Diaz, Ricardo
and
Robins, Sinai
2002.
The Frobenius Problem, Rational Polytopes, and Fourier–Dedekind Sums.
Journal of Number Theory,
Vol. 96,
Issue. 1,
p.
1.