Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-10T09:20:47.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Lie Algebras of Pro-Affine Algebraic Groups

Published online by Cambridge University Press:  20 November 2018

Nazih Nahlus
Nazih Nahlus*
Affiliation:
Mathematics Department, American University of Beirut, Beirut, Lebanon, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the basic theory of Lie algebras of affine algebraic groups to the case of pro-affine algebraic groups over an algebraically closed field 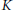$K$ of characteristic 0. However, some modifications are needed in some extensions. So we introduce the pro-discrete topology on the Lie algebra 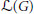$\mathcal{L}(G)$ of the pro-affine algebraic group 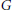$G$ over 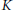$K$, which is discrete in the finite-dimensional case and linearly compact in general. As an example, if 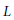$L$ is any sub Lie algebra of 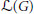$\mathcal{L}(G)$, we show that the closure of 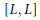$\left[ L,\,L \right]$ in 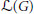$\mathcal{L}(G)$ is algebraic in 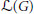$\mathcal{L}(G)$.

We also discuss the Hopf algebra of representative functions 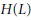$H(L)$ of a residually finite dimensional Lie algebra 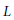$L$. As an example, we show that if 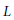$L$ is a sub Lie algebra of 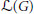$\mathcal{L}(G)$ and 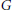$G$ is connected, then the canonical Hopf algebra morphism from 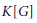$K\left[ G \right]$ into 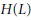$H(L)$ is injective if and only if 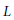$L$ is algebraically dense in 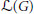$\mathcal{L}(G)$.

Keywords

14L16W17B45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 3 , 01 June 2002 , pp. 595 - 607
Copyright
Copyright © Canadian Mathematical Society 2002

References

[B] Borel, A., Linear algebraic groups. 2nd edition, Graduate Texts in Math. 126, Springer-Verlag, 1991.Google Scholar
[Bk] Bourbaki, N., General Topology. Chapters 1–4, Springer-Verlag, 1989.Google Scholar
[H1] Hochschild, G., Algebraic Lie algebras and representative functions. Illinois J. Math. 3 (1959), 499–523.Google Scholar
[H2] Hochschild, G., Coverings of pro-affine algebraic groups. Pacific J. Math. 35 (1970), 399–415.Google Scholar
[H3] Hochschild, G., Basic theory of algebraic groups and Lie algebras. Graduate Texts in Math. 75, Springer-Verlag, 1981.Google Scholar
[H-M1] Hochschild, G. and Mostow, G. D., Representations and representative functions of Lie groups. Ann. of Math. 66 (1957), 495–542.Google Scholar
[H-M2] Hochschild, G. and Mostow, G. D., Pro-affine algebraic groups. Amer. J. Math. 91 (1969), 1127–1140.Google Scholar
[H-M3] Hochschild, G. and Mostow, G. D., Complex analytic groups and Hopf algebras. Amer. J. Math. 91 (1969), 1141–1151.Google Scholar
[Hu] Humphreys, J. E., Linear algebraic groups. Graduate Texts in Math. 21, Springer-Verlag, 1975.Google Scholar
[Lf] Lefschetz, S., Algebraic topology. AMS Colloquium Publications 27, Amer. Math. Soc., Providence, R.I., 1942.Google Scholar
[Lp] Leptin, H., Linear kompakte modulun und ringe. Math. Z. 62 (1955), 241–267.Google Scholar
[Lu-Ma] Lubotzky, A. and Magid, A., Cohomology of unipotent and pro-unipotent groups. J. Algebra 74 (1982), 76–95.Google Scholar
[Ma1] Magid, A. R., The universal group cover of a pro-affine algebraic group. Duke Math. J. 42 (1975), 43–49.Google Scholar
[Ma2] Magid, A. R., Module categories of analytic groups. Cambridge University Press, 1982.Google Scholar
[N1] Nahlus, N., Representative functions on complex analytic groups. Amer. J. Math. 116 (1994), 621–636.Google Scholar
[N2] Nahlus, N., Basic groups of Lie algebras and Hopf algebras. Pacific J. Math. 180 (1997), 135–151.Google Scholar
[S] Springer, T. A., Linear algebraic groups. 2nd edition, Birkhäuser, 1998.Google Scholar
[W] Waterhouse, W., Introduction to affine group schemes. Graduate Texts in Math. 66, Springer-Verlag, 1979.Google Scholar