No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Recently, Ferus ([5], [6]) classified connected Riemannian manifolds with parallel second fundamental form in a real space form of constant curvature 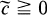 . In this paper we may restrict our attention to isotropic submanifolds with parallel second fundamental form in the Euclidean sphere Sm(k) of constant curvature k. Due to Ferus, we find that an isotropic submanifold with parallel second fundamental form in Sm is locally congruent to one of compact symmetric spaces of rank one and the immersion is locally equivalent to the second or the first standard immersion according as M is a sphere or not. In Section 2, we characterize the first standard immersion of a complex projective space into a sphere in terms of isotropic immersions.
. In this paper we may restrict our attention to isotropic submanifolds with parallel second fundamental form in the Euclidean sphere Sm(k) of constant curvature k. Due to Ferus, we find that an isotropic submanifold with parallel second fundamental form in Sm is locally congruent to one of compact symmetric spaces of rank one and the immersion is locally equivalent to the second or the first standard immersion according as M is a sphere or not. In Section 2, we characterize the first standard immersion of a complex projective space into a sphere in terms of isotropic immersions.