Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amur, Krishna
and
Pujar, S. S.
1978.
Conformality and isometry of Riemannian manifolds to spheres. II.
Journal of Differential Geometry,
Vol. 13,
Issue. 2,
Egorov, I. P.
1980.
Automorphisms in generalized spaces.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 3,
p.
1260.
Aminova, A. V.
1991.
Groups of transformations of Riemannian manifolds.
Journal of Soviet Mathematics,
Vol. 55,
Issue. 5,
p.
1996.


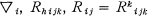 and
and 