Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-19T01:14:09.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Hp-Maximal Regularity and Operator Valued Multipliers on Hardy Spaces

Published online by Cambridge University Press:  20 November 2018

Shangquan Bu  and
Christian Le Merdy
Shangquan Bu
Affiliation:
Department of Mathematical Science, University of Tsinghua, Beijing 100084, P.R. China email: [email protected]
Christian Le Merdy
Affiliation:
Département de Mathématiques, Université de Franche-Comté, 25030 Besançon Cedex, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider maximal regularity in the 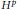${{H}^{p}}$ sense for the Cauchy problem 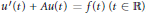${{u}^{\prime }}(t)+Au(t)=f(t)(t\,\in \mathbb{R})$, where 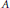$A$ is a closed operator on a Banach space 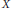$X$ and 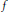$f$ is an 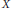$X$-valued function defined on $\mathbb{R}$. We prove that if 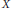$X$ is an AUMD Banach space, then 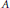$A$ satisfies 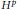${{H}^{p}}$-maximal regularity if and only if 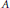$A$ is Rademacher sectorial of type 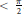$<\frac{\pi }{2}.$ Moreover we find an operator 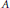$A$ with 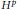${{H}^{p}}$-maximal regularity that does not have the classical 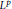${{L}^{p}}$-maximal regularity. We prove a related Mikhlin type theorem for operator valued Fourier multipliers on Hardy spaces 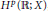${{H}^{p}}(\mathbb{R};\,X)$, in the case when 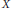$X$ is an AUMD Banach space.

Keywords

42B3047D06Lp-maximal regularityHp-maximal regularityRademacher boundedness
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 6 , 01 December 2007 , pp. 1207 - 1222
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Arendt, W., Semigroups and evolution equations: functional calculus, regularity and kernel estimates. In: Handbook of Differential Equations: Evolutionary Differential Equations, Vol. I, North-Holland, Amsterdam, 2004, pp. 1–85.Google Scholar
[2] Arendt, W. and Bu, S., The operator-valued Marcinkiewicz multiplier theorem and maximal regularity. Math. Z. 240(2002), no. 2, 311–343.Google Scholar
[3] Arendt, W. and Bu, S., Tools for maximal regularity. Math. Proc. Cambridge Phil. Soc. 134(2003), no. 2, 317–336.Google Scholar
[4] Arendt, W. and Bu, S., Operator valued multiplier theorems characterizing Hilbert spaces. J. Aust. Proc. Math. Soc. 77(2004), no. 2, 175–184.Google Scholar
[5] Blasco, O., Hardy spaces of vector valued functions: duality. Trans. Amer. Math. Soc. 308(1988), no. 2, 495–507.Google Scholar
[6] Blasco, O. and Pełczyński, A., Theorems of Hardy and Paley for vector-valued analytic functions and related classes of Banach spaces. Trans. Amer. Math. Soc. 323(1991), no. 1, 335–367.Google Scholar
[7] Blower, G., A multiplier characterization of analytic UMD spaces. Studia Math. 96(1990), no. 2, 117–124.Google Scholar
[8] Burkholder, D., Martingales and singular integrals in Banach spaces. In: Handbook of the Geometry of Banach Spaces, Vol. I. Elsevier, Amsterdam, 2001, pp. 233–269.Google Scholar
[9] Clément, P. and Guerre-Delabrière, S., On the regularity of abstract Cauchy problems and boundary value problems. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 9(1998), no. 4, 245–266.Google Scholar
[10] Clément, P., de Pagter, B., Sukochev, F., and Witvliet, H., Schauder decomposition and multiplier theorems. Studia Math. 138(2000), no. 2, 135–163.Google Scholar
[11] Clément, P. and Prüss, J., An operator valued transference principle and maximal regularity on vector valued Lp -spaces. In: Evolution Equations and Their Applications in Physical and Life Sciences. Lecture Notes in Pure and Appl. Math. 215, Dekker, New York, 2001, pp. 67–78.Google Scholar
[12] Garling, D. J. H., On martingales with values in a complex Banach space. Math. Proc. Cambridge Phil. Soc. 104(1988), no. 2, 399–406.Google Scholar
[13] Garnett, J. B., Bounded Analytic Functions. Pure Appl. Math 96, Academic Press, New York, 1981.Google Scholar
[14] Girardi, M. and Weis, L., Operator-valued martingale transfoms and R-boundedness. Illinois J. Math. 49(2005), no. 2, 487–516. (electronic)Google Scholar
[15] Haagerup, U. and Pisier, G., Factorization of analytic functions with values in non commutative L1-spaces and applications. Canad. J. Math. 41(1989), no. 5, 882–906.Google Scholar
[16] Hytönen, T., Convolution, multipliers and maximal regularity on vector-valued Hardy spaces. J. Evol. Equ. 5(2005), no. 2, 205–225.Google Scholar
[17] Kalton, N. and Lancien, G., A solution to the problem of Lp -maximal regularity. Math. Z. 235(2000), no. 3, 559–568.Google Scholar
[18] Kalton, N. and Weis, L., The H∞ calculus and sums of closed operators . Math. Ann. 321(2001), no. 2, 319–345.Google Scholar
[19] Kunstmann, P. and Weis, L., Maximal Lp-regularity for parabolic equations, Fourier multiplier theorems and H ∞ -functional calculus. In: Functional Analytic Methods for Evolution Equations. Lecture Notes in Math. 1855, 2004, Springer, Berlin, pp. 65–311.Google Scholar
[20] Lancien, F., Lancien, G. and Le Merdy, C., A joint functional calculus for sectorial operators with commuting resolvents. Proc. London Math. Soc. 77(1998), no. 2, 387–414.Google Scholar
[21] Le Merdy, C., Counterexamples on Lp -maximal regularity. Math. Z. 230(1999), no. 1, 47–62.Google Scholar
[22] Le Merdy, C., Two results about H∞ functional calculus on analytic UMD spaces. J. Aust. Math. Soc. 74(2003), no. 3, 351–378.Google Scholar
[23] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. II. Function Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 97, Springer-Verlag, Berlin, 1979.Google Scholar
[24] Stein, E., Classes Hp, multiplicateurs et fonctions de Littlewood-Paley. C. R. Acad. Sci. Paris Sér. A-B 263(1966), A716–A719.Google Scholar
[25] Weis, L., Operator-valued Fourier multiplier theorems and maximal Lp -regularity. Math. Ann. 319(2001), no. 4, 735–758.Google Scholar