Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T09:27:17.091Z Has data issue: false hasContentIssue false
  • English
  • Français

The Groups of the Regular Star-Polytopes

Published online by Cambridge University Press:  20 November 2018

Peter McMullen
Peter McMullen*
Affiliation:
University College London Gower Street London WC1E 6BT England, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The regular star-polyhed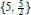ron $\left\{ 5,\,\frac{5}{2} \right\}$ is isomorphic to the abstract polyhedron 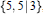$\left\{ 5,\,5|3 \right\}$, where the last entry “3” in its symbol denotes the size of a hole, given by the imposition of a certain extra relation on the group of the hyperbolic honeycomb 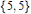$\left\{ 5,\,5 \right\}$. Here, analogous formulations are found for the groups of the regular 4-dimensional star-polytopes, and for those of the non-discrete regular 4-dimensional honeycombs. In all cases, the extra group relations to be imposed on the corresponding Coxeter groups are those arising from “deep holes”; thus the abstract description of 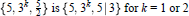$\left\{ 5,\,{{3}^{k}},\,\frac{5}{2} \right\}\,\text{is}\,\left\{ 5,\,{{3}^{k}},\,5|3 \right\}\,\text{for}\,k\,=\,1\,\text{or}\,\text{2}$. The non-discrete quasi-regular honeycombs in 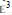${{\mathbb{E}}^{3}}$, on the other hand, are not determined in an analogous way.

Keywords

51M2052C99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 2 , 01 April 1998 , pp. 426 - 448
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Coxeter, H. S.M., Regular skew polyhedra in three and four dimensions, and their topological analogues. Proc. London Math. Soc. (2) 43(1937), 33–62. (Reprinted with changes in Twelve Geometric Essays, Southern Illinois University Press, Carbondale, 1968. 76–105.)Google Scholar
2. Coxeter, H. S. M., Regular Polytopes. Third edition, Dover, New York, 1973.Google Scholar
3. Coxeter, H. S. M. and Moser, W. O. J., Generators and Relations for Discrete Groups. Fourth edition, Springer, 1980.Google Scholar
4. Debrunner, H.E., Dissecting orthoschemes into orthoschemes. Geom. Dedicata 33(1990), 123–152.Google Scholar
5. McMullen, P., Regular star-polytopes, and a theorem of Hess. Proc. London Math. Soc. (3) 18(1968), 577–596.Google Scholar
6. McMullen, P., Realizations of regular polytopes. Aequationes Math. 37(1989), 38–56.Google Scholar
7. McMullen, P., Nondiscrete regular honeycombs. Chapter 10 in: Quasicrystals, Networks, and Molecules of Fivefold Symmetry (Ed. Hargittai, I.), VCH Publishers, New York, 1990. 159–179.Google Scholar
8. McMullen, P., Realizations of regular apeirotopes. Aequationes Math. 47(1994), 223–239.Google Scholar
9. McMullen, P. and Schulte, E., Regular polytopes from twisted Coxeter groups. Math. Z. 201(1989), 209–226.Google Scholar
10. McMullen, P., Constructions for regular polytopes. J. Combinat. Theory A 53(1990), 1–28.Google Scholar
11. McMullen, P., Hermitian forms and locally toroidal regular polytopes. Advances Math. 82(1990), 88–125.Google Scholar
12. McMullen, P., Higher toroidal regular polytopes. Advances Math. 117(1996), 17–51.Google Scholar
13. McMullen, P., Abstract Regular Polytopes (monograph in preparation).Google Scholar
14. Monson, B.R., A family of uniform polytopes with symmetric shadows. Geom. Dedicata 23(1987), 355–363.Google Scholar
15. Schulte, E., Reguläre Inzidenzkomplexe, II. Geom. Dedicata 14(1983), 33–56.Google Scholar
16. Schulte, E., Amalgamations of regular incidence-polytopes. Proc. London Math. Soc. (3) 56(1986), 303–328.Google Scholar
17. Tits, J., Buildings of Spherical Type and Finite BN-Pairs. Lecture Notes in Math. 386, Springer, Berlin, 1974.Google Scholar