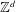Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barlow, M. T.
Croydon, D. A.
and
Kumagai, T.
2021.
Quenched and averaged tails of the heat kernel of the two-dimensional uniform spanning tree.
Probability Theory and Related Fields,
Vol. 181,
Issue. 1-3,
p.
57.
Halberstam, Noah
and
Hutchcroft, Tom
2024.
Logarithmic Corrections to the Alexander–Orbach Conjecture for the Four-Dimensional Uniform Spanning Tree.
Communications in Mathematical Physics,
Vol. 405,
Issue. 10,