Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berenstein, Carlos A.
and
Li, Bao Qin
2004.
Value Distribution Theory and Related Topics.
Vol. 3,
Issue. ,
p.
265.
Zikkos *, E.
2005.
On a theorem of norman levinson and a variation of the fabry gap theorem.
Complex Variables, Theory and Application: An International Journal,
Vol. 50,
Issue. 4,
p.
229.
Li, Bao Qin
2005.
Interpolating varieties for entire functions of minimal type.
Advances in Mathematics,
Vol. 194,
Issue. 1,
p.
87.
Walnut, David F.
2005.
Harmonic Analysis, Signal Processing, and Complexity.
Vol. 238,
Issue. ,
p.
97.
Carando, Daniel
García, Domingo
Maestre, Manuel
and
Sevilla-Peris, Pablo
2009.
A Riemann manifold structure of the spectra of weighted algebras of holomorphic functions.
Topology,
Vol. 48,
Issue. 2-4,
p.
54.
Li, Bao Qin
2010.
On interpolation for Hörmander’s algebras.
Science China Mathematics,
Vol. 53,
Issue. 3,
p.
763.
Zioło, Piotr
2011.
Geometric characterization of interpolation in the space of Fourier–Laplace transforms of ultradistributions of Roumieu type.
Collectanea mathematica,
Vol. 62,
Issue. 2,
p.
161.
Bonet, José
and
Fernández, Carmen
2014.
The Range of the Restriction Map for a Multiplicity Variety in Hörmander Algebras of Entire Functions.
Mediterranean Journal of Mathematics,
Vol. 11,
Issue. 2,
p.
643.
Zikkos, Elias
2015.
Solutions of infinite order differential equations without the grouping phenomenon and a generalization of the Fabry–Pólya theorem.
Journal of Mathematical Analysis and Applications,
Vol. 423,
Issue. 2,
p.
1825.
Zikkos, Elias
2017.
Interpolation in
$$H^{p}$$
H
p
spaces over the right half-plane.
Periodica Mathematica Hungarica,
Vol. 75,
Issue. 2,
p.
368.
Bonet, José
and
Galbis, Antonio
2020.
Invariant Subspaces of the Integration Operators on Hörmander Algebras and Korenblum Type Spaces.
Integral Equations and Operator Theory,
Vol. 92,
Issue. 4,
Bonet, José
2021.
Every Separable Complex Fréchet Space with a Continuous Norm is Isomorphic to a Space of Holomorphic Functions.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 1,
p.
8.


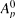 will be obtained in the paper, which as an application will also give a generalization of the well-known Pólya-Levinson density theorem.
will be obtained in the paper, which as an application will also give a generalization of the well-known Pólya-Levinson density theorem.