Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-04T00:53:54.442Z Has data issue: false hasContentIssue false
  • English
  • Français

Genus 2 Curves with Quaternionic Multiplication

Published online by Cambridge University Press:  20 November 2018

Srinath Baba  and
Håkan Granath
Srinath Baba
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montréal, QC, H3G 1M8 e-mail:[email protected]
Håkan Granath
Affiliation:
Department of Mathematics, Karlstad University, 65188 Karlstad, Sweden e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We explicitly construct the canonical rational models of Shimura curves, both analytically in terms of modular forms and algebraically in terms of coefficients of genus 2 curves, in the cases of quaternion algebras of discriminant 6 and 10. This emulates the classical construction in the elliptic curve case. We also give families of genus 2 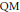$\text{QM}$ curves, whose Jacobians are the corresponding abelian surfaces on the Shimura curve, and with coefficients that are modular forms of weight 12. We apply these results to show that our $j$-functions are supported exactly at those primes where the genus 2 curve does not admit potentially good reduction, and construct fields where this potentially good reduction is attained. Finally, using $j$, we construct the fields of moduli and definition for some moduli problems associated to the Atkin–Lehner group actions.

Keywords

11G1814G35Shimura curvecanonical modelquaternionic multiplicationmodular formfield of moduli
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 4 , 01 August 2008 , pp. 734 - 757
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bolza, O., On binary sextics with linear transformations onto themselves. Amer. J. Math. 10(1887), no. 1, 47–70.Google Scholar
[2] Bruin, N., Flynn, V., J. Gonzáles, and V. Rotger, On finiteness conjectures for endomorphism algebras of abelian surfaces. Math. Proc. Cambridge Philos. Soc. 141(2006), no. 3, 383–408.Google Scholar
[3] Cardona, G., On the number of curves of genus 2 over a finite field. Finite Fields Appl. 9(2003), no. 4, 505–526.Google Scholar
[4] Dieulefait, L. and V. Rotger, The arithmetic of QM-abelian surfaces through their Galois representations. J. Algebra 281(2004), no. 1, 124–143.Google Scholar
[5] Dieulefait, L. and V. Rotger, On abelian surfaces with potential quaternionic multiplication. Bull. Belg. Math. Soc. Simon Stevin 12(2005), no. 4, 617–624.Google Scholar
[6] Elkies, N. D., Shimura curve computations. In: Algorithmic Number Theory. Lecture Notes in Comput. Sci. 1423, Springer, Berlin, 1998, pp. 1–47.Google Scholar
[7] Grayson, D. R. and Stillman, M. E., Macaulay 2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/ Google Scholar
[8] van, G. der Geer, Hilbert Modular Surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 16, Springer-Verlag, Berlin, 1988.Google Scholar
[9] Hiramatsu, T., Eichler maps and hyperbolic Fourier expansion. Nagoya Math. J. 40(1970), 173–192.Google Scholar
[10] Hashimoto, K.-I. and Murabayashi, N., Shimura curves as intersections of Humbert surfaces and defining equations of QM-curves of genus two. Tohoku Math. J. 47(1995), no. 2, 272–296.Google Scholar
[11] Hayashida, T. and Nishi, M., Existence of curves of genus two on a product of two elliptic curves. J. Math. Soc. Japan 17(1965), 1–16.Google Scholar
[12] Hirzebruch, F. and D. Zagier, Intersection numbers of curves on Hilbert modular surfaces and modular forms of Nebentypus Invent.Math. 36(1976), 57–113.Google Scholar
[13] Igusa, J.-I., Arithmetic variety of moduli for genus two, Ann. of Math. 72(1960), 612–649.Google Scholar
[14] W. Jordan, B., On the Diophantine Arithmetic of Shimura Curves. Ph.D. Thesis, Harvard University, 1981.Google Scholar
[15] W. Jordan, B., Points on Shimura curves rational over number fields. J. Reine Angew.Math. 371(1986), 92–114.Google Scholar
[16] Kurihara, A., On some examples of equations defining Shimura curves and the Mumford uniformization. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 25(1979), no. 3, 277–300.Google Scholar
[17] Lange, H. and Birkenhake, C., Complex Abelian Varieties. Grundlehren derMathematischen Wissenschaften 302, Springer-Verlag, Berlin, 1992.Google Scholar
[18] Mestre, J.-F., Construction de courbes de genre 2 à partir de leurs modules. In: Effective Methods in Algebraic Geometry. Progr. Math. 94, Birkhäuser Boston, Boxton,MA, 1991. pp. 313–334.Google Scholar
[19] Ogg, A. P., Real points on Shimura curves. In: Arithmetic and Geometry. Progr. Math. 35, Birkhäuser Boston, Boxton, MA, 1983, pp. 277–307.Google Scholar
[20] RI, P./GP, version 2.1.5, Bordeaux, 2004, Available at http://pari.math.u-bordeaux.fr. Google Scholar
[21] Rodriguez-Villegas, F., Explicit models of genus 2 curves with split CM. In: Algorithmic Number Theory. Lecture Notes in Comput. Sci. 1838, Springer, Berlin, 2000, pp. 505–514.Google Scholar
[22] Rotger, V., Quaternions, polarization and class numbers, J. Reine Angew.Math. 561(2003), 177–197.Google Scholar
[23] Rotger, V., Modular Shimura varieties and forgetful maps. Trans. Amer.Math. Soc. 356(2004), no. 4, 1535–1550.Google Scholar
[24] Rotger, V., The field of moduli of quaternionic multiplication on abelian varieties. Int. J. Math.Math. Sci. 2004no. 49-52, 2795–2808. Corrected version http://arxiv.org/abs/math/0409354. Google Scholar
[25] Shimura, G., Introduction to the Arithmetic Theory of Automorphic Functions. Publications of the Mathematical Society of Japan 11, Princeton University Press, Princeton, NJ, 1971.Google Scholar
[26] Shimura, G., On canonical models of arithmetic quotients of bounded symmetric domains, . Ann. of Math. 91(1970), 144–222.Google Scholar
[27] Shimura, G., Construction of class fields and zeta functions of algebraic curves. Ann. of Math. 85(1967), 58–159.Google Scholar
[28] Vignéras, M.-F., Arithmétique des algèbres de quaternions, Lecture Notes in Mathematics 800, Springer, Berlin, 1980.Google Scholar