Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T07:14:52.130Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Moak's q-Laguerre Polynomials

Published online by Cambridge University Press:  20 November 2018

Roelof Koekoek
Roelof Koekoek*
Affiliation:
Delft University of Technology, Delft, The Netherlands
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

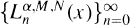In [6] we studied the polynomials which are generalizations of the classical (generalized) Laguerre polynomials 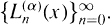These polynomials were shown to be orthogonal on the interval [0, ∞) with respect to the inner product where a > — 1,M ≧0 and N ≧0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 2 , 01 April 1990 , pp. 280 - 303
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Askey, R., Ramanujan s extension of the gamma and beta function, The American Mathematical Monthly 87 (1980), 346–359.Google Scholar
2. Chihara, T.S., An introduction to orthogonal polynomials, Mathematics and Its Applications 13 (Gordon and Breach, N.Y., 1978).Google Scholar
3. Gasper, G. and Rahman, M., Basic hyper geometric series (Cambridge University Press), to appear.Google Scholar
4. Jackson, F.H., On q-definite integrals, Quarterly Journal on Pure and Applied Mathematics 41 (1910), 193–203.Google Scholar
5. Koekoek, J. and Koekoek, R., A simple proof of a differential equation for generalizations of Laguerre polynomials, Delf University of Technology, Faculty of Mathematics and Informatics, report no. 89-15 (1989).Google Scholar
6. Koekoek, R. and Meijer, H.G., A generalization of Laguerre polynomials, Delft University of Technology, Faculty of Mathematics and Informatics, report no. 88-28 (1988). Submitted for publication.Google Scholar
7. Koekoek, R., Koornwinder's generalized Laguerre polynomials and its q-analogues, Delft University of Technology, Faculty of Mathematics and Informatics, report no. 88-87 (1988).Google Scholar
8. Koekoek, R., Koornwinder's Laguerre polynomials, Delft Progress Report 01 (1988), 393–104.Google Scholar
9. Koornwinder, T.H., Orthogonal polynomials with weight , Canadian Mathematical Bulletin 27 (1984), 205–214.Google Scholar
10. Moak, D.S., The q-analogue of the Laguerre polynomials, Journal of Mathematical Analysis and Applications 81 (1981), 20–47.Google Scholar
11. Szegö, G., Orthogonal polynomials, American Mathematical Society, Colloquium Publications 23, 4th edition, Providence, R.I. (1975).Google Scholar