Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:34:14.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalization of Hölder's Theorem to Ordered Modules

Published online by Cambridge University Press:  20 November 2018

T. M. Viswanathan
T. M. Viswanathan*
Affiliation:
Queen's University, Kingston, Ontario The University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hölder's theorem on archimedean groups states:

An ordered (abelian) group G is order isomorphic to an ordered subgroup of the ordered group R of real numbers if and only if it is archimedean.

We comprehend this theorem in the following setting: G is a Z-module and Ris the completion with respect to the open interval topology of the ordered field Q; Qitself is the ordered quotient field of the ordered domain Z.

Rephrasing the situation, we raise the following question: We start with a fully ordered domain A,let Kbe its ordered quotient field. We endow Kwith the open interval topology and consider 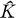, the topological completion of K. Is it possible to impose a compatible order structure on 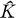and if this can be done, when can we say that an ordered A-module Mis order isomorphic to an ordered A-submodule of 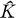? In Theorem 3.1, we obtain a set of necessary and sufficient conditions for this isomorphism to hold.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 149 - 157
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Banaschewski, B., Extensions of topological spaces, Can. Math. Bull. 7 (1964), 1–22.Google Scholar
2. Bourbaki, N., Éléments de mathématique ; Première partie (Fascicule II.) Livre I I I ; Topologie générale, Chapitre 1: Structures topologiques \ Chapitre 2: Structures uniformes-, Actualités Sci. Indust, No. 1142 (Hermann, Paris, 1961).Google Scholar
3. Bourbaki, N., Éléments de mathématique) Première partie (Fascicule III.) Livre I I I ; Topologie générale, Chapitre 3: Groupes topologiques, Actualités Sci. Indust., No. 1143 (Hermann, Paris, 1960).Google Scholar
4. Conrad, P., Methods of ordering a vector space, J. Indian Math. Soc. 22 (1958), 1–25.Google Scholar
5. Conrad, P., On ordered vector spaces, J. Indian Math. Soc. 22 (1958), 27–32.Google Scholar
6. Fuchs, L., Partially ordered algebraic systems (Addison-Wesley, Reading, Massachusetts, 1963).Google Scholar
7. Holder, O., Die Axiome der Quantitdt und die Lehre vom Mass, Ber. Verh. Sachs. Ges. Wiss. Leipzig Math. Phys. CI. 53 (1901), 1–64.Google Scholar
8. Ribenboim, P., Théorie des groupes ordonnés (Universidad National del Sur, Bahia Blanca, 1963).Google Scholar
9. Ribenboim, P., On ordered modules, J. Reine Angew Math. 225 (1967), 120–146.Google Scholar