Article contents
A Forcing Axiom Deciding the Generalized Souslin Hypothesis
Published online by Cambridge University Press: 07 January 2019
Abstract
We derive a forcing axiom from the conjunction of square and diamond, and present a few applications, primary among them being the existence of super-Souslin trees. It follows that for every uncountable cardinal 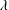 $\unicode[STIX]{x1D706}$, if
$\unicode[STIX]{x1D706}$, if 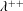 $\unicode[STIX]{x1D706}^{++}$ is not a Mahlo cardinal in Gödel’s constructible universe, then
$\unicode[STIX]{x1D706}^{++}$ is not a Mahlo cardinal in Gödel’s constructible universe, then 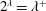 $2^{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}^{+}$ entails the existence of a
$2^{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}^{+}$ entails the existence of a 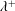 $\unicode[STIX]{x1D706}^{+}$-complete
$\unicode[STIX]{x1D706}^{+}$-complete 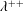 $\unicode[STIX]{x1D706}^{++}$-Souslin tree.
$\unicode[STIX]{x1D706}^{++}$-Souslin tree.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
This research was partially supported by the Israel Science Foundation (grant #1630/14).
References
- 2
- Cited by


