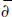Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T16:56:25.277Z Has data issue: false hasContentIssue false
  • English
  • Français

The Explicit Solution of the -Neumann Problem in a Non-Isotropic Siegel Domain

Published online by Cambridge University Press:  20 November 2018

Jingzhi Tie
Jingzhi Tie*
Affiliation:
Department of Mathematics Yale University New Haven, CT 06520-8283 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we solve the 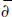-Neumann problem on (0, q) forms, 0 ≤ q ≤ n, in the strictly pseudoconvex non-isotropic Siegel domain: 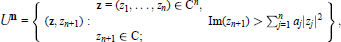where aj > 0 for j = 1,2, . . . , n. The metric we use is invariant under the action of the Heisenberg group on the domain. The fundamental solution of the related differential equation is derived via the Laguerre calculus. We obtain an explicit formula for the kernel of the Neumann operator. We also construct the solution of the corresponding heat equation and the fundamental solution of the Laplacian operator on the Heisenberg group.

Keywords

32F1532F2035N15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 6 , 01 December 1997 , pp. 1299 - 1322
Copyright
Copyright © Canadian Mathematical Society 1997

References

1. Beals, M., Fefferman, C. and Grossman, R., Strictly pseudoconvex domains in Cn. Bull. Amer.Math. Soc. (N.S.) 8(1983), 125–322.Google Scholar
2. Beals, R., B.Gaveau and Greiner, P.C.,Complex Hamiltonian mechanics and parametrices for subelliptic Laplacians. Bull. Sci. Math. 121(1997), 1–36.Google Scholar
3. Beals, R., Gaveau, B., Greiner, P.C. and Vauthier, J., The Laguerre calculus on the Heisenberg group: II. Bull. Sci. Math. 110(1986), 225–288.Google Scholar
4. Beals, R. and Greiner, P.C., Calculus on Heisenberg manifolds. Ann. of Math. Stud. 119, Princeton University Press, Princeton, 1988.Google Scholar
5. Folland, G.B. and Kohn, J.J., The Neumann problem for the Cauchy-Riemann complex. Ann. of Math. Stud. 75, Princeton University Press, Princeton, 1972.Google Scholar
6. Folland, G.B. and Stein, E.M., Estimates for the b-complex and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27(1974), 429–522.Google Scholar
7. Garabedian, P.R. and Spencer, D.C., Complex boundary value problems. Trans. Amer. Math. Soc. 73(1952), 223–242.Google Scholar
8. Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous elliptiques sur certains groupes nilpotents. Acta Math. 139(1977), 95–153.Google Scholar
9. Greiner, P.C., On the Laguerre calculus of left-invariant convolution (pseudo-differential) operators on the Heisenberg group. Séminaire Goulaouic-Meyer-Schwartz 9(1981), 1–39.Google Scholar
10. Greiner, P.C. and Stein, E.M., Estimates for the -Neumann problem. Mathematical Notes Series 19, Princeton University Press, Princeton, 1977.Google Scholar
11. Harvey, F. and Polking, J., The Neumann solution to the inhomogeneous Cauchy-Riemann equations in the unit ball of Cn. Trans. Amer.Math. Soc. 281(1984), 587–613.Google Scholar
12. Hulanicki, A., The distribution of energy in the Brownian motion in the Gaussian field and analytic hypoellipticity of certain subelliptic operators on the Heisenberg group. Studia Math. 56(1976). 165–173.Google Scholar
13. Kimura, K., Kernels for the -Neumann problem on the unit ball in Cn. Comm. Partial Differential Equations (9) 12(1987), 967–1028.Google Scholar
14. Kohn, J.J., Harmonic integrals on strongly pseudo-convex manifolds: I. Ann. of Math. 78(1963). 112–148.Google Scholar
15. Kohn, J.J., Harmonic integrals on strongly pseudo-convex manifolds: II. Ann. ofMath. 79(1964), 450–472.Google Scholar
16. Krantz, S.G., Partial differential equations and complex analysis. tud. Adv. Math., SCRC Press, Boca Raton, 1992.Google Scholar
17. Morrey, C.B. Jr., The analytic embedding of abstract real-analytic manifolds. Ann. of Math. 68(1958), 159–201.Google Scholar
18. Morrey, C.B., The -Neumann problem on strongly pseudo-convex manifolds. In: Differential Analysis, Tata Institute of Fundamental Research, 1964. 81–134.Google Scholar
19. Phong, D.H., On the integral representation for the Neumann operator. Proc. Nat. Acad. Sci. U.S.A. 76(1979), 1554–1558.Google Scholar
20. Rothschild, L.P. and Stein, E.M., Hypoelliptic differential operators and nilpotent groups. Acta Math. 137(1976), 247–320.Google Scholar
21. Stanton, N.K., The heat equation for the -Neumann problem in strictly pseudoconvex Siegel domain: I. J. Anal. Math. 38(1980), 67–112.Google Scholar
22. Stanton, N.K., The heat equation for the -Neumann problem in strictly pseudoconvex Siegel domain: II. J. Anal. Math. 39(1980), 189–301.Google Scholar
23. Stanton, N.K., The solution of the -Neumann problem in strictly pseudoconvex Siegel domain. Invent. Math. 65(1981), 137–174.Google Scholar
24. Taylor, M.E., Noncommutative Harmonic Analysis. Math. Surveys Monographs 22, Amer.Math. Soc., Providence, Rhode Island, 1986.Google Scholar