Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-19T00:47:07.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and Multiplicity of Positive Solutions for Singular Semipositone p-Laplacian Equations

Published online by Cambridge University Press:  20 November 2018

Ravi P. Agarwal ,
Daomin Cao ,
Haishen Lü  and
Donal O'Regan
Ravi P. Agarwal
Affiliation:
Department of Mathematical Sciences, Florida Institute of Technology, Melbourne, FL 32901-6975, U.S.A. e-mail: [email protected]
Daomin Cao
Affiliation:
Institute of Applied Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Science, Beijing 100080, China
Haishen Lü
Affiliation:
Department of Applied Mathematics, Hohai University, Nanjing 210098, China
Donal O'Regan
Affiliation:
Department of Mathematics, National University of Ireland, Galway, Ireland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Positive solutions are obtained for the boundary value problem

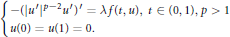$$\left\{ _{u\left( 0 \right)\,=\,u\left( 1 \right)\,=\,0}^{-{{\left( {{\left| {{u}'} \right|}^{p-2}}{u}' \right)}^{\prime }}\,=\,\lambda f\left( t,\,u \right),\,t\,\in \,\left( 0,\,1 \right),\,p\,>\,1} \right.$$

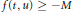Here $f(t,u)\ge -M$, (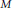$M$ is a positive constant) for $(t,u)\in [0,1]\times (0,\infty )$. We will show the existence of two positive solutions by using degree theory together with the upper–lower solution method.

Keywords

34B15one dimensionalp-Laplacianpositive solutiondegree theoryupper and lower solution
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 449 - 475
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Agarwal, R., Lü, H., and O’Regan, D., Eigenvalues and the one-dimensional p-Laplacian. J. Math. Anal. Appl. 266(2002), no. 2, 383–400.Google Scholar
[2] Agarwal, R., Existence theorems for the one-dimensional singular p-Laplacian equation with sign changing nonlinearities. Appl. Math. Comput. 143(2003), no. 1, 15–38.Google Scholar
[3] Anuradha, V., Hai, D. D. and Shiviji, R., Existence results for superlinear semipositone BVP’s. Proc. Amer.Math. Soc. 124(1996), no. 3, 757–763.Google Scholar
[4] Costa, D. G. and Gonçalves, J. V. A., Existence and multiplicity results for a class of nonlinear elliptic boundary value problems at resonance. J. Math. Anal. Appl. 84(1981), 328–337.Google Scholar
[5] Hai, D. D., Shivaji, R., and Maya, C., An existence result for a class of superlinear p-Laplacian semipositone systems. Differential Integral Equations 14(2001), no. 2, 231–240.Google Scholar
[6] Lü, H. and Zhong, C., A note on singular nonlinear boundary value problems for the one-dimensional p-Laplacian. Appl. Math. Lett. 14(2001), no. 2, 189–194.Google Scholar
[7] Lü, H., O’Regan, D., and Zhong, C., Multiple positive solutions for the one-dimensional singular p-Laplacian. Appl. Math. Comput. 133(2002), no. 2-3, 407–422.Google Scholar
[8] Ma, R., Positive solutions for semipositon. (k, n – k) conjugate boundary value problems. J. Math. Anal. Appl. 252(2000), no. 1, 220–229.Google Scholar
[9] O’Regan, D., Some general existence principle and results for (ϕ(y′))′ = qf(t, y, y′), 0 < t < 1. SIAM J. Math. Anal. 24(1993), no. 3, 648–668.Google Scholar
[10] Wang, J. and Gao, W., A singular boundary value problem for the one-dimensional p-Laplacian. J. Math. Anal. Appl. 201(1996), no. 3, 851–866.Google Scholar
[11] Yao, Q. and Lü, H., Positive solutions of one-dimensional singular p-Laplace equations. Acta Math. Sinica, 41(1998), no. 6, 1253–1264.Google Scholar