Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T04:45:57.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic Averages for Weight Functions Moved by Non-Linear Transformations on ℝn

Published online by Cambridge University Press:  20 November 2018

David I. McIntosh
David I. McIntosh*
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec, H3A 2K6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℝ+ denote the non-negative half of the real line, and let λ denote Lebesgue measure on the Borel sets of ℝn. A function φ: ℝn → ℝ+ is called a weight function if ʃℝn φ dλ = 1. Let (X, ℱ, μ) be a non-atomic, finite measure space, let ƒ: X → ℝ+, and suppose { Tν}ν∊ℝn is an ergodic, aperiodic ℝn-flow on X. We consider the weighted ergodic averages 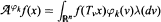where 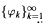is a sequence of weight functions. Sufficient as well as necessary and sufficient conditions for the pointwise, almost-everywhere convergence of 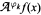are developed for a particular class of weight functions φk. Specifically, let {τk: ℝn → ℝn} be a sequence of measurable, non-singular maps with measurable, non-singular inverses such that the Radon-Nikodym derivatives dλ oτk /dλ and dλ oτk-1 / dλ are L∞ (ℝn), and such that τk and τ-1 map bounded sets to bounded sets. We examine convergence for the sequence where θk is an a.e.-convergent sequence of weight functions which are dominated by a fixed L1(ℝn) function with bounded support.

Keywords

28D9960F99maximal ergodic theorems
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 4 , 01 August 1995 , pp. 852 - 876
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Akçoglu, M.A., and Del, A. Junco, Convergence of Averages of Point Transformations, Proc. Amer. Math. Soc. 49(1975), 265–266.Google Scholar
2. Akçoglu, M.A., Del, A. Junco, and Lee, W. M. F., A Solution to a Problem of A. Bellow, Collection: Almost everywhere convergence, II, Evanston, Illinois, 1989. 1–7. Academic Press, Boston, Massachusetts, 1991.Google Scholar
3. Akçoglu, M.A., and Déniel, Y., Moving Weighted Averages, Canad. J. Math. 45(1993), 449–469.Google Scholar
4. Bellow, A., Jones, R., and Rosenblatt, J., Convergence for Moving Averages, Ergodic Theory Dynamical Systems 10(1990), 43–62.Google Scholar
5. Bellow, A., Harmonic Analysis and Ergodic Theory, Collection: Almost everywhere convergence, Columbus, Ohio, 1988. 73–98. Academic Press, Boston, Massachusetts, 1989.Google Scholar
6. Bellow, A., Almost Everywhere Convergence of Powers, Collection: Almost everywhere convergence, Columbus, Ohio, 1988. 99–120. Academic Press, Boston, Massachusetts, 1989.Google Scholar
7. Broise, M., Déniel, Y. and Derriennic, Y., Réarrangement, Inégalités Maximales et Théorèmes Ergodiques Fractionnaires, Ann. Inst. Fourier (Grenoble) 39(1989), 689–714.Google Scholar
8. Broise, M., Maximal Inequalities and Ergodic Theorems for Cesàro-a or Weighted Averages, Collection: Almost everywhere convergence, II, Evanston, Illinois, 1989. 93–107. Academic Press, Boston, Massachusetts, 1991.Google Scholar
9. Calderôn, A.P., Ergodic theory and translation-invariant operators, Proc. Nat. Acad. Sci. 59(1968), 349–353.Google Scholar
10. Coifman, R., and Weiss, G., Analyse Harmonique Non-commutative sur Certains Espaces Homogènes, Lecture Notes in Math. 242, Springer-Verlag, 1971.Google Scholar
11. Eggleston, H.G., Convexity, Cambridge Tracts in Math, and Mathematical Physics, 47, Cambridge Univ. Press, Cambridge, 1958.Google Scholar
12. Jones, R.L. and Olsen, J., Multi-Parameter Moving Averages, Collection: Almost everywhere convergence, II, Evanston, Illinois, 1989. 127–149. Academic Press, Boston, Massachusetts, 1991.Google Scholar
13. Jones, R.L., Multiparameter Weighted Ergodic Theorems, preprint.Google Scholar
14. Krengel, U., Ergodic Theorems, de Gruyter Studies in Math. 6, W. de Gruyter, 1985.Google Scholar
15. Lind, D.A., Locally Compact Measure Preserving Flows, Adv. in Math. 15(1975), 175–193.Google Scholar
16. Mcintosh, D.I., Ergodic Averages For Weight Functions Moved by Non-Linear Transformations on W, Ph.D. Thesis, University of Toronto, 1993.Google Scholar
17. Nagel, A., and Stein, E.M., On Certain Maximal Functions and Approach Regions, Adv. in Math. 54(1984), 83–106.Google Scholar
18. Nguyen, X.X. and Zessin, H., Ergodic Theorems for Spatial Processes, Z. Wahrscheinlichkeitstheorie verw. Geb. 48(1979), 133–158.Google Scholar
19. Rosenblatt, J., and Wierdl, M., A New Maximal Inequality and its Applications, Ergodic Theory Dynamical Systems 12(1992), 509–558.Google Scholar
20. Rudin, W., Real and Complex Analysis, second edition, Tata McGraw-Hill Publishing, New Delhi, India, 1974.Google Scholar
21. Sueiro, J., A note on maximal operators of Hardy-Littlewood type, Math. Proc. Cambridge Philos. Soc. 102(1987), 131–134.Google Scholar
22. Tempel'man, A.A., Ergodic Theorems for General Dynamical Systems, Trudy Moskov. Mat. Obshch. 26(1972), Trans. Moscow Math. Soc. 26(1972), 94–132.Google Scholar