Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T16:57:04.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Engel Congruences in Groups of Prime-Power Exponent

Published online by Cambridge University Press:  20 November 2018

N. D. Gupta  and
M. F. Newman
N. D. Gupta
Affiliation:
The University of Manitoba, Winnipeg, Manitoba
M. F. Newman
Affiliation:
The Australian National Universityt Canberra, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

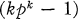It is a well-known result of Sanov (5) that groups of exponent pk (p prime) satisfy the th Engel congruence (definition below). Recently, an alternative proof of this has been given by Glauberman, Krause, and Struik (3). Bruck (2) has conjectured that such groups satisfy the th Engel congruence. In this note we go some way towards proving this.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 1321 - 1323
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Bachmuth, S. and Mochizuki, H. Y., Cyclotomic ideals in group rings, Bull. Amer. Math. Soc. 72 (1966), 1018–1020.Google Scholar
2. Bruck, R. H., On the restricted Burnside problem, Arch. Math. 13 (1962), 179–186.Google Scholar
3. Glauberman, George, Krause, Eugene F., and Rebekka Struik, Ruth, Engel congruences in groups of prime-power exponent, Can. J. Math. 18 (1966), 579–588.Google Scholar
4. Gupta, N. D., Newman, M. F., and Tobin, S. J., On metabelian groups of prime-power exponent, Proc. Roy. Soc. London Ser. A 802 (1968), 237–242.Google Scholar
5. Sanov, I. N., On a certain system of relations in periodic groups with period a power of a prime number, Izv. Akad. Nauk SSSR Ser. Mat. 15 (1951), 477–502.Google Scholar
6. Tobin, Seán, On a theorem of Baer and Higman, Can. J. Math. 8 (1956), 263–270.Google Scholar