Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T00:54:35.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Endomorphisms of Kronecker Modules Regulated by Quadratic Algebra Extensions of a Function Field

Published online by Cambridge University Press:  20 November 2018

F. Okoh  and
F. Zorzitto
F. Okoh
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI, 48202 e-mail:[email protected]
F. Zorzitto
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Kronecker modules, 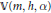$\mathbb{V}\left( m,h,\alpha \right)$, where 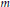$m$ is a positive integer, 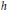$h$ is a height function, and $\alpha $ is a 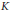$K$-linear functional on the space 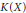$K(X)$ of rational functions in one variable 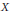$X$ over an algebraically closed field 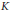$K$, are models for the family of all torsion-free rank-2 modules that are extensions of finite-dimensional rank-1 modules. Every such module comes with a regulating polynomial 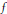$f$ in 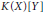$K(X)[Y]$. When the endomorphism algebra of 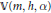$\mathbb{V}\left( m,h,\alpha \right)$ is commutative and non-trivial, the regulator 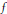$f$ must be quadratic in $Y$. If 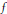$f$ has one repeated root in 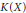$K(X)$, the endomorphism algebra is the trivial extension 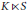$K\ltimes S$ for some vector space 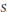$S$. If 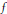$f$ has distinct roots in 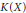$K(X)$, then the endomorphisms form a structure that we call a bridge. These include the coordinate rings of some curves. Regardless of the number of roots in the regulator, those End 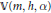$\mathbb{V}\left( m,h,\alpha \right)$ that are domains have zero radical. In addition, each semi-local End 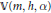$\mathbb{V}\left( m,h,\alpha \right)$ must be either a trivial extension 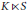$K\ltimes S$ or the product 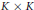$K\times K$.

Keywords

16S5015A27
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 4 , 01 August 2008 , pp. 923 - 957
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Auslander, M., Reiten, I., and Smalø, S. O., Representation Theory of Artin Algebras. Cambridge Studies in Advanced Mathematics 36, Cambridge University Press, 1995.Google Scholar
[2] Eakin, P., A note on finite-dimensional subrings of polynomial rings. Proc. Amer.Math. Soc. 31(1972), 75–80.Google Scholar
[3] Fixman, U., On algebraic equivalence between pairs of linear transformations. Trans. Amer.Math. Soc. 113(1964), 424–453.Google Scholar
[4] Fixman, U. and Okoh, F., Extensions of modules characterized by finite sequences of linear functionals. Rocky Mountain J. Math. 21(1991), no. 4, 1235–1258.Google Scholar
[5] Fossum, R., Griffith, P., and Reiten, I., Trivial Extensions of Abelian Categories. Homological Algebra of Trivial Extensions of Abelian Categories with Applications to Ring Theory. Lecture Notes in Mathematics 456, Springer-Verlag, Berlin, 1975.Google Scholar
[6] Göbel, R. and Simson, D., Embeddings of Kronecker modules into the category of prinjective modules and the endomorphism ring problem. Colloq. Math. 75(1998), no. 2, 213–244.Google Scholar
[7] Göbel, R. and Simson, D., Rigid families and endomorphism algebras of Kronecker modules. Israel J. Math. 110(1999), 293–315.Google Scholar
[8] Lawrence, J., Okoh, F., and F. Zorzitto, Rational functions and Kronecker modules. Comm. Algebra 14(1986), no. 10, 1947–1965.Google Scholar
[9] Lenzing, H., Homological transfer from finitely presented to infinite modules, In: Abelian Group Theory. Lecture Notes in Math. 1006, Springer, Berlin, 1983, pp. 734–761.Google Scholar
[10] McKinnon, D. and Roth, M., Curves arising from endomorphism rings of Kronecker modules. Rocky Mountain J. Math. 37(2007), no. 3, 879–892.Google Scholar
[11] Okoh, F., Indecomposable rank-two modules over some Artinian ring. J. LondonMath. Soc. 22(1980), no. 3, 411–422.Google Scholar
[12] Okoh, F., Some properties of purely simple modules. I. J. Pure Appl. Algebra 27(1983), no. 1, 39–48.Google Scholar
[13] Okoh, F. and Zorzitto, F. A., Subsystems of the polynomial system. Pacific J. Math 109(1983), no. 2, 437–455.Google Scholar
[14] Okoh, F. and Zorzitto, F. A., Extensions that are submodules of their quotients. Canad. Math. Bull. 33(1990), no. 1, 93–99.Google Scholar
[15] Okoh, F. and Zorzitto, F. A., A family of commutative endomorphism algebras. J. Algebra 201(1998), no. 2, 501–527.Google Scholar
[16] Okoh, F. and Zorzitto, F. A., Curves arising from Kronecker modules. Linear Algebra. Appl. 365(2003), 311–348.Google Scholar
[17] Okoh, F. and Zorzitto, F. A., Commutative endomorphism algebras of torsion-free, rank-two Kronecker modules with singular height functions. Rocky Mountain J. Math. 32(2002), no. 4, 1559–1576.Google Scholar
[18] Okoh, F. and Zorzitto, F. A., Commutative algebras of rational function matrices as endomorphisms of Kronecker modules. I. Linear Algebra Appl. 374(2003), 41–62.Google Scholar
[19] Okoh, F. and Zorzitto, F. A., Commutative algebras of rational function matrices as endomorphisms of Kronecker modules. II. Linear Algebra Appl. L 374(2003), 63–85.Google Scholar
[20] Okoh, F. and Zorzitto, F. A., Endomorphism algebras of Kronecker modules regulated by quadratic function fields. Canad. J. Math. 59(2007), no. 1, 186–210.Google Scholar
[21] Ringel, C. M., Infinite-dimensional representations of finite-dimensional algebras. Symposia Mathematica 23(1979), 321–412.Google Scholar
[22] Ringel, C. M., Representation of K-species and bimodules. J. Algebra 41(1976), no. 2, 269–302.Google Scholar
[23] Ringel, C. M., Tame algebras are wild. Algebra Colloq. 6(1999), no. 4, 473–490.Google Scholar
[24] Ringel, C. M., Infinite length modules. Some examples as introduction. In: Infinite LengthModules. Birkhäuser, Basel, 2000, pp. 1–73.Google Scholar
[25] Simson, D., An endomorphism algebra realization problem and Kronecker embeddings for algebras of infinite representation type. J. Pure Appl. Algebra 172(2002), no. 2-3, 293–303.Google Scholar
[26] Simson, D., On Corner type Endo-Wild algebras. J. Pure Appl. Algebra 202(2005), no. 1-3, 118–132.Google Scholar
[27] Thomas, S., The classification problem for torsion-free abelian groups of finite rank. J. Amer. Math. Soc 16(2003), no. 1, 233–258.Google Scholar