Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cailleau, Annie
and
Renault, Guy
1970.
Anneau associ� � une somme directe infinie de modules quasi-injectifs.
Archiv der Mathematik,
Vol. 21,
Issue. 1,
p.
561.
Rutter, Edgar A.
1971.
$PF$-modules.
Tohoku Mathematical Journal,
Vol. 23,
Issue. 2,
Mikhalev, A. V.
and
Skornyakov, L. A.
1972.
Algebra and Geometry.
p.
59.
Zelmanowitz, J.
1973.
Semiprime modules with maximum conditions.
Journal of Algebra,
Vol. 25,
Issue. 3,
p.
554.
Jeremy, Louis
1974.
Modules Et Anneaux Quasi-Continus.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 2,
p.
217.
Rangaswamy, K. M.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
595.
Rangaswamy, K. M.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
595.
Goodearl, K. R.
1976.
Direct sum properties of quasi-injective modules.
Bulletin of the American Mathematical Society,
Vol. 82,
Issue. 1,
p.
108.
Mikhalev, A. V.
1976.
Endomorphism rings of modules and lattices of submodules.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 6,
p.
786.
Faith, Carl
1976.
Algebra II Ring Theory.
Vol. 191,
Issue. ,
p.
61.
Faith, Carl
1985.
The maximal regular ideal of self-injective and continuous rings splits off.
Archiv der Mathematik,
Vol. 44,
Issue. 6,
p.
511.
Dung, Nguyen V.
and
Smith, Patrick F.
1992.
On semi-artinian V-modules.
Journal of Pure and Applied Algebra,
Vol. 82,
Issue. 1,
p.
27.
Huisgen-Zimmermann, Birge
2000.
Infinite Length Modules.
p.
331.
Khurana, Dinesh
and
Srivastava, Ashish K.
2007.
Unit sum numbers of right self-injective rings.
Bulletin of the Australian Mathematical Society,
Vol. 75,
Issue. 3,
p.
355.
OSOFSKY, BARBARA L.
PARK, JAE KEOL
and
RIZVI, S. TARIQ
2010.
PROPERTIES OF INJECTIVE HULLS OF A RING HAVING A COMPATIBLE RING STRUCTURE.
Glasgow Mathematical Journal,
Vol. 52,
Issue. A,
p.
121.
Abrudan, Horea Florian
2011.
On regular endomorphism rings of topological Abelian groups.
Czechoslovak Mathematical Journal,
Vol. 61,
Issue. 2,
p.
521.
Guil Asensio, Pedro A.
and
Srivastava, Ashish K.
2013.
Automorphism-invariant modules satisfy the exchange property.
Journal of Algebra,
Vol. 388,
Issue. ,
p.
101.
Birkenmeier, Gary F.
Park, Jae Keol
and
Rizvi, S. Tariq
2013.
Extensions of Rings and Modules.
p.
19.
Quynh, Truong Cong
Abyzov, Adel Nailevich
and
Trang, Dao Thi
2022.
Rings all of whose finitely generated ideals are automorphism-invariant.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 08,
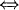 for any set of orthogonal idempotents
for any set of orthogonal idempotents 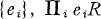 is an essential extension of
is an essential extension of  . This note extends these results to endomorphism rings of quasi-injective modules.
. This note extends these results to endomorphism rings of quasi-injective modules.

