Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-15T12:47:11.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Edge Partition Properties of Graphs

Published online by Cambridge University Press:  20 November 2018

C. Ward Henson
C. Ward Henson*
Affiliation:
Duke University, Durham, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Erdös and Hajnal [1] have introduced an edge partition relation for graphs

(1)

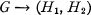
which means that whenever the edges of G are separated into two sets, E1 and E2, there exists a subgraph G’ of G such that G’ is isomorphic to Hi and the edges of G’ are all in Ei. for i = 1 or 2. A class of graphs 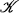has the G-R (Galvin-Ramsey) property [2] if for each H in 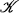there exists a G in 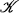which satisfies G→(H,H).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 3 , June 1973 , pp. 603 - 610
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Erdös, P. and Hajnal, A., On decomposition of graphs, Acta Math. Acad. Sci. Hungar. 18 (1967), 359–377.Google Scholar
2. Erdös, P. and Hajnal, A., Problems and results infinite and infinite combinatorial analysis, Ann. of New York Acad, of Sci. 175 (1970), 115–124.Google Scholar
3. Ghouila-Houri, A., Charactérisation des graphs non orientés dont on peut orienter les aretes de manière à obtenir le graph d'une relation d'ordre, C.R. Acad. Sci. Paris, Sér. A-B 254 (1962), 1370–1371.Google Scholar
4. Gilmore, P. C. and Hoffman, A. J., A characterization of comparability graphs and of interval graphs, Can. J. Math. 16 (1964), 539–548.Google Scholar