Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-26T07:16:08.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Division par un polynôme hyperbolique

Published online by Cambridge University Press:  20 November 2018

Jacques Chaumatet  and
Anne-Marie Chollet
Jacques Chaumatet
Affiliation:
U.M.R. 8628, Bâtiment 425, Université Paris-Sud, 91405 OrsayCedex, France e-mail: [email protected]
Anne-Marie Chollet
Affiliation:
U.M.R. 8524, Bâtiment M2, Université des Sciences et Technologies de Lille, 59655 Villeneuve d’Ascq Cedex, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On se donne un intervalle ouvert non vide 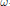$\omega $ de $\mathbb{R}$, un ouvert connexe non vide $\Omega $ de 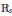${{\mathbb{R}}_{5}}$ et unpolynôme unitaire

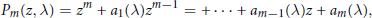$${{P}_{m}}\left( z,\text{ }\!\!\lambda\!\!\text{ } \right)={{z}^{m}}+{{a}_{1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right){{z}^{m-1}}=+\cdot \cdot \cdot +{{a}_{m-1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)z+{{a}_{m}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)$$

de degré 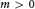$m>0$, dépendant du paramètre 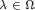$\lambda \in \Omega $. Un tel polynôme est dit 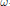$\omega $-hyperbolique si, pour tout 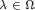$\lambda \in \Omega $, ses racines sont réelles et appartiennent à 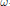$\omega $.

On suppose que les fonctions 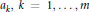${{a}_{k}},k=1,\cdot \cdot \cdot ,m$, appartiennent à une classe ultradifférentiable 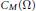${{C}_{M}}\left( \Omega \right)$. On s‘intéresse au problème suivant. Soit 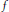$f$ appartient à 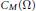${{C}_{M}}\left( \Omega \right)$, existe-t-il des fonctions 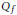${{Q}_{f}}$ et 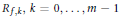${{R}_{f,k}},k=0,\cdot \cdot \cdot ,m-1$, appartenant respectivement à 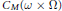${{C}_{M}}\left( \omega \,\times \,\Omega \right)$ et à 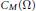${{C}_{M}}\left( \Omega \right)$, telles que l’on ait, pour 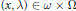$\left( x,\,\lambda \right)\,\in \,\omega \,\times \,\Omega$,

$$f\left( x \right)={{P}_{m}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right){{Q}_{f}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right)+\sum\limits_{k=0}^{m-1}{{{x}^{k}}{{R}_{f,k}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)?}$$

On donne ici une réponse positive dès que le polynôme est 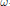$\omega$-hyperbolique, que la class untradifférentiable soit quasi-analytique ou non ; on obtient alors, des exemples d’idéaux fermés dans 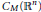${{C}_{M}}\left( {{\mathbb{R}}^{n}} \right)$ . On complète ce travail par une généralisation d’un résultat de C. L. Childress dans le cadre quasi-analytique et quelques remarques.

Abstract

Abstract

Let 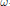$\omega $ be an open interval in $\mathbb{R}$$\Omega $, an open connected set in 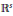${{\mathbb{R}}^{s}}$ and 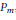${{P}_{m}}$ , a monic polynomial

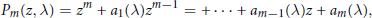$${{P}_{m}}\left( z,\text{ }\!\!\lambda\!\!\text{ } \right)={{z}^{m}}+{{a}_{1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right){{z}^{m-1}}=+\cdot \cdot \cdot +{{a}_{m-1}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)z+{{a}_{m}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)$$

of degree 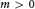$m>0$, depending on 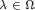$\lambda \in \Omega $. Such a polynomial is said to be 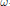$\omega $-hyperbolic if, for any 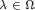$\lambda \in \Omega $, its roots are real and contained in 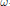$\omega$.

Let us suppose that 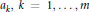${{a}_{k}},k=1,\cdot \cdot \cdot ,m$, belong to an ultradifferentiable class 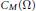${{C}_{M}}\left( \Omega \right)$. We deal with the following problem. Given 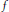$f$ belonging to 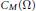${{C}_{M}}\left( \Omega \right)$, do there exist functions 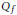${{Q}_{f}}$ and 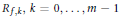${{R}_{f,k}},k=0,\cdot \cdot \cdot ,m-1$ belonging respectively to 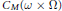${{C}_{M}}\left( \omega \,\times \,\Omega \right)$ and to 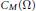${{C}_{M}}\left( \Omega \right)$, such that we have, for 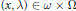$\left( x,\,\lambda \right)\,\in \,\omega \,\times \,\Omega$,

$$f\left( x \right)={{P}_{m}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right){{Q}_{f}}\left( x,\text{ }\!\!\lambda\!\!\text{ } \right)+\sum\limits_{k=0}^{m-1}{{{x}^{k}}{{R}_{f,k}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)?}$$

We give here a positive answer as soon as the polynomial is 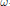$\omega $-hyperbolic whether the ultradifferentiable class is quasi-analytic or not; we then get examples of closed ideals in 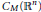${{C}_{M}}\left( {{\mathbb{R}}^{n}} \right)$. We complete this work with a generalization of a result of C. L. Childress in the quasi-analytic case and some remarks.

Keywords

26E1046E2546J20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 6 , 01 December 2004 , pp. 1121 - 1144
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Alekseevsky, D., Kriegl, A., Michor, P.W. and Losik, M., Choosing roots of polynomials smoothly. Israel J. Math. 105(1998), 203–233.Google Scholar
[2] Bronshtein, M.D., Smoothness of roots of polynomials depending on parameters. Siberian J. Math. 20(1979), 347–352.Google Scholar
[3] Bronshtein, M.D., Division with remainder in spaces of smooth functions. Trans. Moscow Math. Soc. (1990), 109–138.Google Scholar
[4] Chaumat, J. et Chollet, A.M., Surjectivité de l’application restriction à un compact dans des classes de fonctions ultradifférentiables. Math. Ann. 298(1994), 7–40.Google Scholar
[5] Chaumat, J., Sur le théorème de division de Weierstrass. Studia Math. 116(1995), 59–84 Google Scholar
[6] Chaumat, J., Caractérisation des anneaux noethériens de séries formelles à croissance contrôlées. Application à la synthèse spectrale. Publicationes Mat. 41(1997), 545–561.Google Scholar
[7] Childress, C.L., Weierstrass division in quasianalytic local rings. Can. J. Math. 28(1976), 938–953.Google Scholar
[8] Dynkin, E.M., Pseudoanalytic extension of smooth functions. The uniform scale. Amer. Math. Soc. Trans. 115(1980), 33–58.Google Scholar
[9] Hörmander, L., The analysis of linear partial differential operators I. 2ième édition, Springer-Verlag, Berlin, 1989.Google Scholar
[10] Malgrange, B., Ideals of differentiable functions. Oxford, Oxford Université Press, 1966.Google Scholar
[11] Petzsche, H.J., On E. Borel's theorem. Math. Ann. 63(1988), 71–88.Google Scholar
[12] Thilliez, V., On closed ideals in smooth classes. Math. Nachr. 227(2001), 143–157.Google Scholar
[13] Thilliez, V., A sharp division estimate for ultradifferentiable germs. Pac. J. Math. 205(2002), 337–256.Google Scholar
[14] Thilliez, V., Bounds for quotients in rings of formal power series with growth constraints. Studia Math. 151(2002), 49–65.Google Scholar
[15] Tougeron, J.C., Idéaux de fonctions différentiables. Springer-Verlag, Berlin, 1972.Google Scholar
[16] Wakabayashi, S., Remarks on hyperbolic polynomials. Tsukuba J. Math. 10(1986), 17–28.Google Scholar
[17] Alekseevsky, D., Kriegl, A., Michor, P.W. et Losik, M., Choosing roots of polynomials smoothly, II. Israel J. Math. 139(2003), 183–188.Google Scholar