Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T18:23:12.504Z Has data issue: false hasContentIssue false
  • English
  • Français

A Distortion Theorem for Analytic Maps of Annuli

Published online by Cambridge University Press:  20 November 2018

C. E. Castonguay  and
H. G. Helfenstein
C. E. Castonguay
Affiliation:
University of Ottawa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every abstract open Riemann surface can be made "concrete" (in the terminology of (1)) by considering it as a covering surface (in general branched) of the complex plane 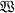by means of a suitable projection map p. Since this covering map is not unique, it seems natural to single out some such maps by an extremal property. The use of Riemannian metrics compatible with the conformai structure on the given surface 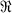for the study of $1 is well known ; from the point of view of differential geometry it suggests an investigation of the distortion caused by p between such a metric ds^ and the Euclidean metric of .

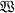Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 185 - 198
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Behnke, H. and Sommer, F., Théorie der analytischen Funktionen einer komplexen Verdnderlichen (Berlin, 1955).Google Scholar
2. Busemann, H., The geometry of geodesies (New York, 1955).Google Scholar
3. Castonguay, C. E. and Helfenstein, H. G., On analytic maps of the pseudosphere, Monatsh. Math., 68 (1964), 97–101.Google Scholar
4. Erdélyi, A., Higher transcendental functions (New York, 1953).Google Scholar
5. Helfenstein, H. G., Conformai maps with least distortion, Can. J. Math., 7 (1955), 306–313.Google Scholar
6. Nevanlinna, R., Eindeutige analytische Funktionen (Berlin, 1936).Google Scholar
7. Nevanlinna, R., TJnifor mister ung (Berlin, 1953).Google Scholar
8. Steffenson, T. F., Interpolation (New York, 1927).Google Scholar
9. Torstov, G. P., Fourier series (New Jersey, 1962).Google Scholar