Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T08:53:49.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Decaying Solutions Of 2mth Order Elliptic Problems

Published online by Cambridge University Press:  20 November 2018

W. Allegretto  and
L. S. Yu
W. Allegretto
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta T6G 2G1
L. S. Yu
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a semilinear elliptic problem 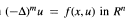, (n > 2m). Under suitable conditions on f, we show the existence of a decaying positive solution. We do not employ radial arguments. Our main tools are weighted spaces, various applications of the Mountain Pass Theorem and LP regularity estimates of Agmon. We answer an open question of Kusano, Naito and Swanson [Canad. J. Math. 40(1988), 1281-1300] in the superlinear case: 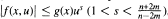, and improve the results of Dalmasso [C. R. Acad. Sci. Paris 308(1989), 411-414] for the case .

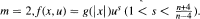Keywords

35J6035J35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 3 , 01 June 1991 , pp. 449 - 460
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Adams, R.A., Sobolev spaces. Academic Press, New York, 1975.Google Scholar
2. Agmon, S., The Lp approach to the Dirichlet problem, Ann. Scuola Norm. Sup. Pisa 13(1959), 405–448.Google Scholar
3. Allegretto, W. and Huang, Y.X., On positive solutions of a class of fourth order elliptic systems, Funk. Ekvac. 32(1989), 57–65.Google Scholar
4. Allegretto, W. and Yu, L.S., Positive If solutions of subcritical nonlinear problems, J. Diff. Equations, to appear.Google Scholar
5. Bernis, F., Elliptic and parabolic semilinear problems without conditions at infinity, Arch. Rat. Mech. Anal. 106(1989), 217–241.Google Scholar
6. Dalmasso, R., Solutions positives globales d'une equation biharmonique sur-linéaire, C.R. Acad. Sci. Paris 308(1989), 411–414.Google Scholar
7. Dalmasso, R. , Solutions d'équations elliptiques semilinearies d'ordre 2m, Funkcial Ekvac, to appear.Google Scholar
8. Fukagai, N., Positive entire solutions of higher order semilinear elliptic equations, Hiroshima Math. J. 17(1987), 561–590.Google Scholar
9. Gilbarg, D. and Trudinger, N.S., Elliptic partial differential equations of second order. 2nd edition, Springer- Verlag, Berlin-Heidelberg-New York-Tokyo, 1983.Google Scholar
10. Kusano, T., Naito, M. and Swanson, C.A., Radial entire solutions to even order semilinear elliptic equations in the plane, Proc. Roy. Soc. Edinburgh 105A(1987), 275–287.Google Scholar
11. Kusano, T., Naito, M. and Swanson, C.A., Entire solutions of a class of even order quasilinear elliptic equations, Math. Z. 195(1987), 151–163.Google Scholar
12. Kusano, T., Naito, M. and Swanson, C.A., Radial entire solutions of even order semilinear elliptic equations, Can. J. Math. XL(1988), 1281–1300.Google Scholar
13. Kusano, T. and Swanson, C.A., Positive entire solutions of semilinear biharmonic equations, Hiroshima Math. J. 17(1987), 13–28.Google Scholar
14. Maz'ja, V.G., Sobolev Spaces. Springer-Verlag, Berlin-Heildelberg-New York-Tokyo, 1985.Google Scholar
15. Rabinowitz, P.H., Minimax methods in critical point theory with applications to differential equations. Amer. Math. Soc, Providence, R.I., 1986.Google Scholar
16. Usami, H., On strongly increasing entire solutions of even order semilinear elliptic equations, Hiroshima Math. J. 17(1987), 175–217.Google Scholar