Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-04T19:02:32.069Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Perturbations of Reflexive Algebras

Published online by Cambridge University Press:  20 November 2018

Kenneth R. Davidson
Kenneth R. Davidson*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study lattice properties of operator algebras which are invariant under compact perturbations. It is easy to see that if 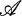and 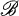are two operator algebras with 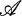contained in 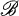, then the reverse inclusion holds for their lattices of invariant subspaces. We will show that in certain cases, the assumption thats 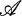is contained in 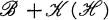, where 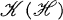is the ideal of compact operators, implies that the lattice of 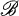is “approximately” contained in the lattice of 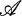. In particular, suppose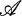d and 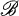are reflexive and have commutative subspace lattices containing “enough” finite dimensional elements. We show (Corollary 2.8) that if 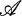is unitarily equivalent to a subalgebra of 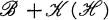, then there is a unitary operator which carries all “sufficiently large” subspaces in lat 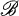into lat .

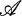Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 685 - 700
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Arveson, W. B., Interpolation in nest algebras, J. Func. Anal. 20 (1972), 208–233.Google Scholar
2. Davidson, K. R., Commutative subspace lattices, Indiana Univ. Math. J. 27, 479–490.Google Scholar
3. Davidson, K. R. and Fong, C. K., An operator algebra which is not closed in the Calkin algebra, Pac. J. Math. 72, 57–58.Google Scholar
4. Fall, T., Arveson, W. and Muhly, P., Perturbations of nest algebras, J. Oper. Th. 1. Google Scholar
5. Halmos, P. R., Quasitriangular operators, Acta Sci. Math. (Szeged) 29 (1968), 283–293.Google Scholar
6. Hopenwasser, A. and Plastiras, J., Isometries of quasitriangular operator algebras, to appear.Google Scholar
7. Johnson, B. E. and Parrot, S. K., Operators commuting with a von Neumann Algebra modulo the set of compact operators, J. Func. Anal. 11 (1972), 39–61.Google Scholar
8. Plastiras, J., Quasitriangular operator algebras, Pac. J. Math. 64 (1976), 543–549.Google Scholar
9. Plastiras, J., Compact perturbations of certain von Neumann algebras, Trans. AMS 234 (1977), 561–577.Google Scholar