Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wilson, Jeremy
1974.
On Outer-Commutator Words.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 3,
p.
608.
Hartley, Brian
1979.
Subgroups of finite index in profinite groups.
Mathematische Zeitschrift,
Vol. 168,
Issue. 1,
p.
71.
Roman'kov, V. A.
1982.
Width of verbal subgroups in solvable groups.
Algebra and Logic,
Vol. 21,
Issue. 1,
p.
41.
Raphael, Deborah
1996.
Commensurability and elementary equivalence of polycyclic groups.
Bulletin of the Australian Mathematical Society,
Vol. 53,
Issue. 3,
p.
425.
Григорчук, Ростислав Иванович
and
Grigorchuk, Rostislav Ivanovich
1996.
Ограниченные когомологии групповых конструкций.
Математические заметки,
Vol. 59,
Issue. 4,
p.
546.
Grigorchyuk, R. I.
1996.
Bounded cohomology of group constructions.
Mathematical Notes,
Vol. 59,
Issue. 4,
p.
392.
Bardakov, V. G.
1997.
On a width of verbal subgroups of certain free constructions.
Algebra and Logic,
Vol. 36,
Issue. 5,
p.
288.
Chapuis, Olivier
1998.
On the theories of free solvable groups.
Journal of Pure and Applied Algebra,
Vol. 131,
Issue. 1,
p.
13.
Smirnova, E. G.
2000.
The width of a power of a free nilpotent group of nilpotency class 2.
Siberian Mathematical Journal,
Vol. 41,
Issue. 1,
p.
173.
Faĭziev, Valeriĭ
2000.
Functional Equations and Inequalities.
p.
77.
Faiziev, Valerii
2001.
A problem of expressibility in some amalgamated products of groups.
Journal of the Australian Mathematical Society,
Vol. 71,
Issue. 1,
p.
105.
Faĭziev, Valeriĭ A.
and
Sahoo, Prasanna K.
2002.
Pseudocharacters and the Problem of Expressibility for Some Groups.
Journal of Algebra,
Vol. 250,
Issue. 2,
p.
603.
AKHAVAN-MALAYERI, MEHRI
and
RHEMTULLA, AKBAR
2003.
PRODUCTS OF COMMUTATORS IN FREE GROUPS.
International Journal of Algebra and Computation,
Vol. 13,
Issue. 02,
p.
231.
Nies, André
2003.
Separating Classes of Groups by First-Order Sentences.
International Journal of Algebra and Computation,
Vol. 13,
Issue. 03,
p.
287.
AKHAVAN-MALAYERI, MEHRI
2005.
ON COMMUTATOR LENGTH OF CERTAIN CLASSES OF SOLVABLE GROUPS.
International Journal of Algebra and Computation,
Vol. 15,
Issue. 01,
p.
143.
Nikolov, Nikolay
and
Segal, Dan
2007.
Direct products and profinite completions.
Journal of Group Theory,
Vol. 10,
Issue. 6,
Alizadeh Sanati, Mahboubeh
and
Skoruppa, Nils-Peter
2008.
Commutator Length of Finitely Generated Linear Groups.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2008,
Issue. 1,
Gupta, Ch. K.
and
Timoshenko, E. I.
2011.
Universal theories for partially commutative metabelian groups.
Algebra and Logic,
Akhavan-Malayeri, Mehri
and
Krieg, Aloys
2011.
On Solvable Groups of Arbitrary Derived Length and Small Commutator Length.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Timoshenko, E. I.
2013.
The commutator width of elements in a wreath product of free abelian groups.
Siberian Mathematical Journal,
Vol. 54,
Issue. 5,
p.
926.
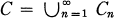 so that a group G ∊ C if and only if G ∊ Cn for some n.
so that a group G ∊ C if and only if G ∊ Cn for some n.