No CrossRef data available.
Article contents
Coding Ergodic Processes to Approximate Bernoulli Processes
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In [1] Ornstein defined a metric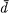 
on processes which, for processes (P, τ) and (Q, σ) with equal numbers of atoms, measures how closely the motions of P and Q under r and a, respectively, imitate each other. If we think of (P, τ) and (Q, σ) as stationary stochastic processes, and we assume (P, τ) and (Q, σ) are ergodic, then 
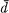((P, τ)(Q, σ)) < α says that with probability one a printout from (P, r) can be changed on a set of integers with density less than a to obtain a printout from (Q, σ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Ornstein, D. S., An application of ergodic theory to probability theory, Ann. Probability 1, (1973), 43–65.Google Scholar
2.
Ornstein, D. S., Bernoulli shifts with the same entropy are isomorphic,
Advances in Math.
4 (1970), 337–352.Google Scholar
3.
Ornstein, D. S., Factors of Bernoulli shifts are Bernoulli shifts,
Advances in Math.
5 (1970), 349–364.Google Scholar
4.
Shields, P. C., The theory of Bernoulli shifts (The University of Chicago Press, 1973).Google Scholar
5.
Smorodinsky, M., Ergodic theory, entropy, Springer Lecture Notes in Mathematics, No. 214 (1971).Google Scholar
You have
Access