Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T09:27:23.822Z Has data issue: false hasContentIssue false
  • English
  • Français

The Chern–Ricci Flow on Oeljeklaus–Toma Manifolds

Published online by Cambridge University Press:  20 November 2018

Tao Zheng
Tao Zheng*
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 100081, People's Republic of China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

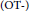We study the Chern-Ricci flow, an evolution equation of Hermitian metrics, on a family of Oeljeklaus–Toma $\left( \text{OT-} \right)$ manifolds that are non-Kähler compact complex manifolds with negative Kodaira dimension. We prove that after an initial conformal change, the flow converges in the Gromov–Hausdorff sense to a torus with a flat Riemannian metric determined by the 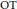$\text{OT}$-manifolds themselves.

Keywords

53C4453C5532W2032J1832M17Chern-Ricci flowOeljeklaus-Toma manifoldCalabi-type estimateGromov–Hausdorff convergence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 1 , 01 February 2017 , pp. 220 - 240
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Battisti, L. and Oeljeklaus, K., Holomorphic line bundles over domains in Cousin groups and the algebraic dimension of Oeljeklaus-Toma manifolds. Proc. Edinb. Math. Soc. (2) 58(2015), no. 2, 273–285. http://dx.doi.org/10.1017/S0013091514000327 Google Scholar
[2] Borevich, A. I. and Shafarevich, I. R., Number theory. Pure and Applied Mathematics, 20, Academic Press,New York-London, 1966.Google Scholar
[3] Cheng, S. Y. and Yau, S.-T., Differential equations on Riemannian manifolds and their geometric applications. Comm. Pure Appl. Math. 28(1975), no. 3, 333–354.http://dx.doi.org/10.1002/cpa.3160280303 Google Scholar
[4] Dragomir, S. and Ornea, L., Locally conformally Kahler geometry. Progress in Mathematics, 155, Birkhauser Boston, Inc., Boston, MA, 1998.http://dx.doi.org/10.1007/978-1-4612-2026-8 Google Scholar
[5] Fang, S., Tosatti, V., Weinkove, B., and Zheng, T., Inoue surfaces and the Chern-Ricci flow.arxiv:1 501.07578Google Scholar
[6] Fong, F. T.-H. and Zhang, Z., The collapsing rate of the Kahler-Ricci flow with regular infinite time singularity. J. Reine Angew. Math. 703(2015), 95–113. http://dx.doi.Org/10.1515/crelle-2O13-0043Google Scholar
[7] Gallot, S., Hulin, D., and Lafontaine, J., Riemannian geometry. Third ed., Universitext. Springer-Verlag, Berlin, 2004. http://dx.doi.org/10.1007/978-3-642-18855-8 Google Scholar
[8] Gill, M., Convergence of the parabolic complex Monge-Ampére equation on compact Hermitian manifolds. Comm. Anal. Geom. 19(2011), no. 2, 277–303.http://dx.doi.org/10.4310/CAC.2011.v19.n2.a2 Google Scholar
[9] Gill, M.,Collapsing of products along the Kâhler-Ricci flow. Trans. Amer. Math. Soc. 366(2014), no. 7, 3907–3924.http://dx.doi.org/10.1090/S0002-9947-2013-06073-4 Google Scholar
[10] Gill, M., The Chern-Ricci flow on smooth minimal models of general type.arxiv:1307.0066Google Scholar
[11] Gill, M. and Smith, D. J., The behavior of Chern-Ricci scalar curvature under Chern-Ricci flow. 43(2015), no. 11, 4875–4883. http://dx.doi.Org/10.1090/proc/12745Google Scholar
[12] Inoue, M., On surfaces of Class VII0, Invent. Math. 24(1974), 269–310. http://dx.doi.org/10.1007/BF01425563Google Scholar
[13] Kasuya, H., Vaisman metrics on solvmanifolds and Oeljeklaus-Toma manifolds. Bull. Lond. Math.Soc. 45(2013), no. 1, 15–26. http://dx.doi.Org/10.1112/blms/bdsO57 Google Scholar
[14] Moerdijk, I. and Mrcun, J., Introduction to foliations and Lie groupoids. Cambridge Studies in Advanced Mathematics, 91, Cambridge University Press, Cambridge, 2003. http://dx.doi.Org/10.1017/CBO9780511615450 Google Scholar
[15] Nie, X., Regularity of a complex Monge-Ampére equation on Hermitian manifolds. Comm. Anal.Geom. 22(2014), no. 5, 833–856. http://dx.doi.org/10.4310/CAC.2014.v22.n5.a3 Google Scholar
[16] Oeljeklaus, K. and Toma, M., Non-Kähler compact complex manifolds associated to number fields. Ann. Inst. Fourier(Grenoble) 55(2005), no. 1,161–171. http://dx.doi.Org/10.58O2/aif.2O93 Google Scholar
[17] Ornea, L. and Verbitsky, M., Oeljeklaus-Toma manifolds admitting no complex subvarieties. Math. Res. Lett. 18(2011), no. 4, 747–754. http://dx.doi.Org/10.4310/MRL.2011.v18.n4.a12 Google Scholar
[18] Ornea, L. and Vuletescu, V., Oeljeklaus-Toma manifolds and locally conformally Kähler metrics. A state of the art. Stud. Univ. Babes-Bolyai. Math. 58(2013), no. 4, 459–468.Google Scholar
[19] Parton, M. and Vuletescu, V., Examples of non-trivial rank in locally conformai Kähler geometry. Math. Z. 270(2012), no. 1-2, 179–187. http://dx.doi.org/10.1007/s00209-010-0791-5 Google Scholar
[20] Phong, D. H., Sesum, N., and Sturm, J.,Multiplier ideal sheaves and the Kähler-Ricci flow. Comm. Anal. Geom. 15(2007), no. 3, 613–632.http://dx.doi.org/10.4310/CAC.2007.v15.n3.a7 Google Scholar
[21] Phong, D. H. and Sturm, J., The Dirichlet problem for degenerate complex Monge-Ampére equations. Comm. Anal. Geom. 18(2010), no. 1, 145–170. http://dx.doi.org/10.4310/CAC.2010.v18.n1.a6 Google Scholar
[22] Sesum, N. and Tian, G., Bounding scalar curvature and diameter along the Kähler-Ricci flow (after Perelman). J. Inst. Math. Jussieu 7(2008), no. 3, 575–587. http://dx.doi.Org/10.1017/S1474748008000133 Google Scholar
[23] Sherman, M. and Weinkove, B., Local Calabi and curvature estimates for the Chern-Ricci flow. New York J. Math. 19(2013),565–582.Google Scholar
[24] Song, J. and Tian, G., The Kähler-Ricci flow on surfaces of positive Kodaira dimension. Invent. Math. 170(2007), no. 3, 609–653.http://dx.doi.org/10.1007/s00222-007-0076-8 Google Scholar
[25] Song, J.,Canonical measures and Kähler-Ricci flow. J. Amer. Math. Soc. 25(2012), no. 2, 303–353. http://dx.doi.Org/10.1090/S0894-0347-2011-00717-0 Google Scholar
[26] Song, J., Bounding scalar curvature for global solutions of the Kähler-Ricci flow. arxiv:1111.5681Google Scholar
[27] Song, J. and Weinkove, B., An introduction to the Kähler-Ricci flow. In: An introduction to the Khler-Ricci flow, Lecture Notes in Math., 2086, Springer, Cham., 2013, pp. 89–188.http://dx.doi.Org/10.1007/978-3-319-00819-6_3Google Scholar
[28] Streets, J. and Tian, G., A parabolic flow ofpluriclosed metrics. Int. Math. Res. Not. IMRN 2010(2010), no. 16, 3103–3133. http://dx.doi.org/10.1093/imrn/rnp237 Google Scholar
[29] Tricerri, F., Some examples of locally conformai Kähler manifolds. Rend. Sem. Mat. Univ. Politec.Torino 40(1982), no. 1, 81–92.Google Scholar
[30] Tosatti, V. and Weinkove, B., On the evolution of a Hermitian metric by its Chern-Ricci form. J.Differential Geom. 99(2015), no. 1,125–163.Google Scholar
[31] Tosatti, V., The Chern-Ricci flow on complex surfaces. Compos. Math. 149(2013), no. 12, 2101–2138. http://dx.doi.Org/10.1112/S0010437X13007471 Google Scholar
[32] Tosatti, V., Weinkove, B., and Yang, X., Collapsing of the Chern-Ricci flow on elliptic surfaces. Math. Ann. 362(2015), no. 3-4, 1223–1271. http://dx.doi.Org/10.1007/s00208-014-1160-1 Google Scholar
[33] Tosatti, V., The Kähler-Ricci flow, Ricci-flat metrics and collapsing limits. arxiv:1408.0161Google Scholar
[34] Verbitsky, S., Curves on Oeljeklaus-Toma manifolds. arxiv:1111.3828Google Scholar
[35] Tosatti, V., Surfaces on Oeljeklaus-Toma manifolds. 0 arxiv:1306.2456Google Scholar
[36] Vuletescu, V., LCK metrics on Oeljeklaus-Toma manifolds versus Kronecker's theorem. Bull. Math. Soc. Sci. Math. Roumanie (N. S.) 57(105)(2014), no. 2, 225–231.Google Scholar
[37] Yau, S.-T., A general Schwarz lemma for Kähler manifolds. Amer. J. Math. 100(1978), no. 1, 197–203.http://dx.doi.org/10.2307/2373880 Google Scholar