Article contents
Calderón–Zygmund Operators Associated to Ultraspherical Expansions
Published online by Cambridge University Press: 20 November 2018
Abstract
We define the higher order Riesz transforms and the Littlewood-Paley  $g$-function associated to the differential operator
$g$-function associated to the differential operator 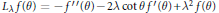 ${{L}_{\lambda }}f(\theta )\,=\,-{f}''(\theta )-2\lambda \cot \theta {f}'(\theta )+{{\lambda }^{2}}f(\theta )$. We prove that these operators are Calderón–Zygmund operators in the homogeneous type space
${{L}_{\lambda }}f(\theta )\,=\,-{f}''(\theta )-2\lambda \cot \theta {f}'(\theta )+{{\lambda }^{2}}f(\theta )$. We prove that these operators are Calderón–Zygmund operators in the homogeneous type space 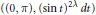 $((0,\,\pi ),\,{{(\sin t)}^{2\lambda }}dt)$. Consequently,
$((0,\,\pi ),\,{{(\sin t)}^{2\lambda }}dt)$. Consequently, 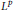 ${{L}^{p}}$ weighted,
${{L}^{p}}$ weighted, 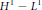 ${{H}^{1}}\,-\,{{L}^{1}}$ and
${{H}^{1}}\,-\,{{L}^{1}}$ and 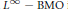 ${{L}^{\infty }}\,-\,BMO$ inequalities are obtained.
${{L}^{\infty }}\,-\,BMO$ inequalities are obtained.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 7
- Cited by


