No CrossRef data available.
Article contents
Bundles on 
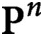$\textbf{P}^n$ with vanishing lower cohomologies
Published online by Cambridge University Press: 24 April 2020
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We study bundles on projective spaces that have vanishing lower cohomologies using their short minimal free resolutions. We partition the moduli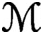 
$\mathcal{M}$
according to the Hilbert function H and classify all possible Hilbert functions H of such bundles. For each H, we describe a stratification of
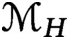$\mathcal{M}_H$
by quotients of rational varieties. We show that the closed strata form a graded lattice given by the Betti numbers.
Keywords
MSC classification
- Type
- Article
- Information
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- © Canadian Mathematical Society 2020
References
Atiyah, M. On the Krull-Schmidt theorem with application to sheaves. Bull. Soc. Math. France 84(1956), 307–317.CrossRefGoogle Scholar
Barth, W. Moduli of vector bundles on the projective plane. Invent. Math. 42(1977), 63–91.CrossRefGoogle Scholar
Bohnhorst, G. and Spindler, H. The stability of certain vector bundles on
${\textbf{P}}^n$
. In: Complex algebraic varieties (Bayreuth, 1990, Lecture Notes in Math., 1507, Springer, Berlin, 1992, pp. 39-50.CrossRefGoogle Scholar
${\textbf{P}}^n$
. In: Complex algebraic varieties (Bayreuth, 1990, Lecture Notes in Math., 1507, Springer, Berlin, 1992, pp. 39-50.CrossRefGoogle ScholarDionisi, C. and Maggesi, M. Minimal resolution of general stable rank-2 vector bundles on
${\textbf{P}}^2$
. Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (8) 6(2003), 151–160.Google Scholar
${\textbf{P}}^2$
. Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (8) 6(2003), 151–160.Google ScholarDrezet, J.-M. and Le Potier, J. Fibrés stables et fibrés exceptionnels sur
${\textbf{P}}^2$
(French. English summary) [Stable bundles and exceptional bundles on
${\textbf{P}}^2$
]. Ann. Sci. École Norm. Sup. (4) 18(1985), no. 2, 193–243.CrossRefGoogle Scholar
${\textbf{P}}^2$
(French. English summary) [Stable bundles and exceptional bundles on
${\textbf{P}}^2$
]. Ann. Sci. École Norm. Sup. (4) 18(1985), no. 2, 193–243.CrossRefGoogle ScholarEagon, J. A. and Northcott, D. G.
Ideals defined by matrices and a certain complex associated with them
. Proc. Roy. Soc. Ser. A 269(1962), 188–204.Google Scholar
Eisenbud, D. Commutative algebra. With a view toward algebraic geometry. Graduate Texts in Mathematics, 150, Springer-Verlag, New York, 1995.Google Scholar
Ellingsrud, G. and Strømme, S. A. On the rationality of the moduli space for stable rank-2 vector bundles on
${\textbf{P}}^2$
. In: Singularities, representation of algebras, and vector bundles (Lambrecht, 1985), Lecture Notes in Math., 1273, Springer, Berlin, 1987, pp. 363–371.CrossRefGoogle Scholar
${\textbf{P}}^2$
. In: Singularities, representation of algebras, and vector bundles (Lambrecht, 1985), Lecture Notes in Math., 1273, Springer, Berlin, 1987, pp. 363–371.CrossRefGoogle ScholarEvans, E. G. and Griffith, P. The syzygy problem. Ann. of Math. (2) 114(1981), no. 2, 323–333.CrossRefGoogle Scholar
Giusti, M. and Merle, M. Singularités isolées et sections planes de variétés déterminantielles. II. Sections de variétés déterminantielles par les plans de coordonnées. In: Algebraic geometry (La Rábida, 1981), Lecture Notes in Math., 961, Springer, Berlin, 1982, pp. 103–118.Google Scholar
Grayson, D. and Stillman, M. Macaulay2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Grothendieck, A. Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatriéme partie. Publications mathématiques de l’I.H.É.S., 32(1967), 5–361.
Google Scholar
Hartshorne, R. Stable vector bundles of rank 2 on
${\textbf{P}}^3$
. Math. Ann. 238(1978), no. 3, 229–280.CrossRefGoogle Scholar
${\textbf{P}}^3$
. Math. Ann. 238(1978), no. 3, 229–280.CrossRefGoogle ScholarHartshorne, R. Varieties of small codimension in projective space. Bull. Amer. Math. Soc. 80 (1974), 1017–1032.CrossRefGoogle Scholar
Hartshorne, R. Algebraic vector bundles on projective spaces: a problem list. Topology 18(1979), no. 2, 117–128.CrossRefGoogle Scholar
Horrocks, G. and Mumford, D. A rank 2 vector bundle on
${\textbf{P}}^4$
with 15,000 symmetries. Topology 12 (1973), 63–81.CrossRefGoogle Scholar
${\textbf{P}}^4$
with 15,000 symmetries. Topology 12 (1973), 63–81.CrossRefGoogle ScholarHulek, K. Stable rank-2 vector bundles on
${\textbf{P}}^2$
with
$\;{c}_1\;$
odd. Math. Ann. 242(1979), no. 3, 241–266.CrossRefGoogle Scholar
${\textbf{P}}^2$
with
$\;{c}_1\;$
odd. Math. Ann. 242(1979), no. 3, 241–266.CrossRefGoogle ScholarMaruyama, M. Stable vector bundles on an algebraic surface. Nagoya Math. J. 58(1975), 25–68.CrossRefGoogle Scholar
Maruyama, M. Moduli of stable sheaves. II. J. Math. Kyoto Univ. 18(1978), no. 3, 557–614.Google Scholar
Maruyama, M. The rationality of the moduli spaces of vector bundles of rank 2 on
${\textbf{P}}^2$
. With an appendix by Isao Naruki. Adv. Stud. Pure Math., 10, Algebraic geometry, Sendai, 1985, North-Holland, Amsterdam, 1987, 399–414.Google Scholar
${\textbf{P}}^2$
. With an appendix by Isao Naruki. Adv. Stud. Pure Math., 10, Algebraic geometry, Sendai, 1985, North-Holland, Amsterdam, 1987, 399–414.Google ScholarSerre, J. P. Algèbre locale. Multiplicités. (French) Cours au Collège de France, 1957 –1958, rédigé par Pierre Gabriel. 2nd ed., Lecture Notes in Math., 11, Springer-Verlag, Berlin-New York, 1965.
Google Scholar
Zhang, M. Bundles On Pn, a Macaulay2 Package. https://math.berkeley.edu/myzhang/Macaulay2/BundlesOnPn.m2.Google Scholar
You have
Access
Open access